Next post Previous post

Unintended Consequences of Math

February 17, 2010 at 11:30 PM by Dr. Drang

I thought last week’s episode of In Our Time was particularly good, even though I already knew most of the facts presented and disagreed with much of the discussion of those facts. Actually, maybe I liked it because I disagreed with it. It gave me a lot to think about, which thinking I will now inflict on you.

In Our Time is a weekly radio show broadcast on BBC Radio 4, the hifalutin BBC station. People outside the UK can get the podcast. Each episode covers a fairly restricted topic, with panel discussion moderated and prodded by the host, Melvyn Bragg. Unlike most American shows of this type, In Our Time puts real experts on its panels, not journalists hawking their latest books. Each show’s panel is usually made up of professors of the subject from various British universities. The scope of the show is immense, as you can see from looking at its archive. The most recent three shows, for example, covered

It’s this last one that got me thinking.

Most of the show was given over to stories, told in the style of James Burkes’ Connections series, of concepts developed purely for their own mathematical beauty (that’s the pure math of the episode’s title) that suddenly became useful for practical purposes decades or centuries later.

The first of these stories, told by the delightfully-named Colva Roney-Dougal of the University of St. Andrews, purportedly explains how the solution of cubic equations led to the electric chair. In the 16th century, while investigating the solution of cubic equations, Cardano found square roots of negative numbers in his solutions. This led to the use of complex numbers. It turned out, hundreds of years later, that complex numbers were very convenient in the analysis of alternating current.

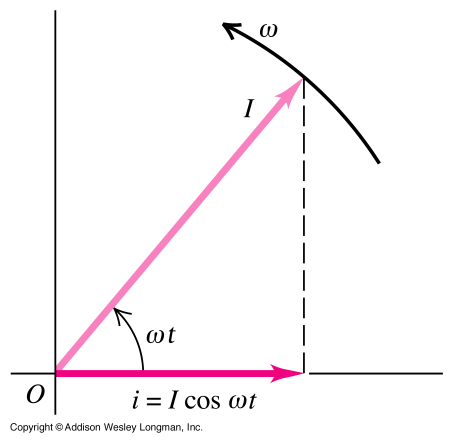(Phasor image blatantly stolen from here.)

If you know anything about the competition between Thomas Edison and George Westinghouse over use of DC and AC, you can see where this is going. As part of his campaign against AC, Edison touted its use in electrocution.1 Therefore, we’re supposed to think, the electric chair was an unintended consequence of complex numbers.

But, and this is pointed out in the show, while complex numbers make the analysis of AC easier, they’re not required. In fact, the electric chair was first designed before anyone used complex numbers to analyze AC. So yes, it’s interesting that complex numbers can be used in AC analysis (as they can be used similarly to analyze mechanical vibrations and problems in plane elasticity), but it really isn’t right to call the connection a consequence.

The use of the term consequence is even less apt in the second example: the application of conic sections to celestial orbits and the trajectories of projectiles. There’s no question this is an interesting connection. The Greeks studied conic sections for their intrinsic beauty, and it was definitely an exercise in pure math. There’s no particular reason to believe they’d be applicable to gravity-controlled motions. But again, this isn’t a consequence, it’s a discovery. Planets didn’t start orbiting in ellipses because Kepler said so.

(Image from Duk at Wikipedia.)

The third story eventually works its way (via Cardano and de Moivre) to Gauss’s use of the normal distribution to predict the position of an asteroid. The asteroid had been observed for only a short time before the view of it was blocked by the sun. Gauss recognized that the observations prior to its disappearance had errors that followed the normal distribution and was able to give the best prediction of where it would be after it reappeared.

The normal distribution had been described by previous mathematicians—de Moivre and Laplace, in particular—studying games of chance and other random phenomena, and Gauss’s use of it to analyze observational errors was definitely a consequence of that earlier work. But here I would disagree with the characterization of that earlier work as pure math. Early studies of probability were intensely practical because of their connection to gambling. There was nothing pure about it.

I would classify the fourth connection, between non-Euclidean geometry and relativity, as I did the conic section/orbit connection: interesting but not a consequence because there’s no cause and effect relation.

The last story, finally, does what all the stories were supposed to do: it describes how the study of prime numbers, once thought of as the purest of pure math topics, now has a very practical and thoroughly unexpected application in cryptography, keeping our credit card numbers safe as we shop online. The historical connection between the pure math and the practical application wasn’t made very strongly—it was basically some hand-waving about Alan Turing—but the story may have been rushed because the show was nearly over.

I was amazed that the show finished without a single mention of “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” a famous paper written in 1960 by a physicist, Eugene Wigner. (How famous is this paper? Type “unreasonable” into your browser’s Google search field and see what comes up. It was the seventh suggestion when I tried it.)

The theme of the paper, as you can guess from the title, is how amazing it is that mathematics—often developed for completely different purposes—works so well to describe the physical world. While the In Our Time episode’s theme is not exactly the same as this, it’s damned close. Even the episode’s title is an echo of the paper’s title.

Fairly early in the show, one of the guests,2 John Barrow of the University of Cambridge, dives right into the main topic of “Unreasonable Effectiveness,” giving a very reasonable explanation of why many topics in math have applicability beyond their original conception. In his view, the whole of math is a collection of patterns, with the number of patterns increasing as math has progressed. It is, therefore, not surprising that some of these patterns match the patterns found in nature. How Barrow manages to go through this explanation without mentioning Wigner’s paper, I’ll never understand, but this was my favorite part of the show.

I doubt I’ll have as much to say about this week’s episode, but I bet I’ll enjoy it.

  1. No, I’m not going to link to the video of the electrocution of Topsy the elephant. I’m sure you can find it on your own if you really want to see it. ↩

  2. Occasional listeners of In Our Time know that the guest panel consists of three experts and may be wondering who the third guest is. Regular listeners will have guessed that it’s Marcus du Sautoy of Oxford, who seems to appear on every BBC show on math. ↩

Next post Previous post