Trussed up
June 11, 2010 at 9:29 PM by Dr. Drang
June is Physical Science and Mechanics Month at Make magazine, and about a week ago Gareth Branwyn of Make asked me to answer one of the Ask Make questions a reader sent in: How do roof trusses distribute the load? This topic is, in fact, right in my wheelhouse, so after some guidance on how long the answer should be, I wrote up a short piece and sent it in. Make posted it yesterday, and I decided to put it here, too, so I’d have my own copy.
Trusses, like all structures, are devices for transferring loads from where you don’t want them to where you do. A roof truss takes the weight of the roof—and the snow on the roof if you live in that kind of climate—and transfers it out into the load-bearing walls of your house. A bridge truss takes the weight of the cars and trucks passing over it and transfers it to the piers. What makes a truss different from other structures—rafters, say, for a roof; or arches for a bridge—is the clever and efficient way it carries the load. Trusses tend to be very lightweight because they take advantage of geometry and the laws of statics.
Geometry
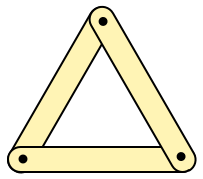
Imagine you have a set of flat sticks, like popsicle sticks or tongue depressors, and you drill holes at the ends of every stick so you can connect them with little bolts. If you connect three sticks together in a triangle, you get a structure that stays rigid even if you don’t tighten the bolts much.
If, on the other hand, you make a square with four sticks, it will be almost impossible to keep the structure from turning into a rhombus when you push on it, no matter how much tightening you do.
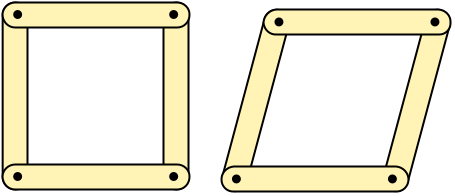
Unlike the triangle, the rigidity of this structure depends on the rigidity of the connections. To really keep a square rigid, you need to add a diagonal brace to create two triangles within the square.
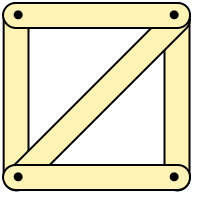
This inherent rigidity of triangles is a geometric property. The triangle is the only polygon whose internal angles—and, therefore, shape—are uniquely defined by the lengths of its sides. There’s nothing like the side-side-side congruence postulate or the law of cosines for higher order polygons.
So if you want to make a structure that’s rigid regardless of the rigidity of its connections, you start with a triangle and build onto it by adding sticks to make more triangles. That, in a nutshell, is a truss.
Laws of statics
An ideal truss is like our assembly of popsicle sticks: a set of straight members or elements, pinned together at their ends, with forces applied only at the joints. (We’ll get to the relation between real trusses and ideal ones in a bit.) Under these conditions, each member in a truss is loaded only at its ends. Some of the loads may be coming from the externally applied forces, and others will be coming from the members to which it’s connected, but whatever their source, the loads are acting exclusively at the ends.
Applying the equations of statics, we can show that if a body is loaded at two points only, the resultant forces at those points
- are equal in magnitude;
- are opposite in direction; and
- act along the line between the two points.
For our truss members, this means that forces on the members are axial (that is, they act along the axis of the member), putting them in either pure tension or pure compression.
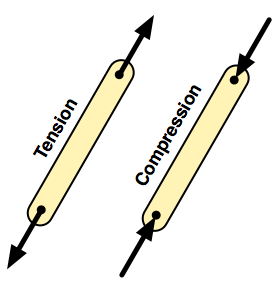
In trusses loaded by downward forces, the members along the top (the “top chord”) are in compression and the members along the bottom (the “bottom chord”) are in tension. The members connecting the top and bottom chords (the “web members”) may be tension or compression, depending on their angles and the distribution of the loads.
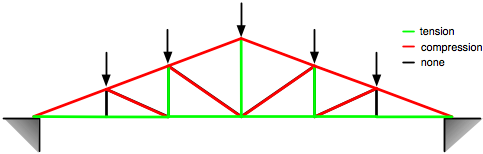
The forces in the members can be calculated in several ways. The traditional “by hand” methods are the method of joints and the method of sections. For truss analysis via computer, the finite element method is the standard technique.
Efficiency
The fact that the forces on each truss member are axial is the key to a truss’s efficiency. In an axially-loaded member, the force is carried equally by every part of the member—no part is wasted.
Contrast this to a beam. When you load a beam at the center, the stresses are much higher there than anywhere else. The material away from the center just isn’t doing as much work, lowering the efficiency of the structure.
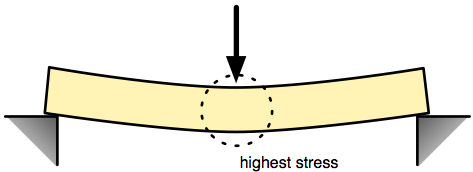
You have, by the way, an instinctive understanding of this. If someone hands you a pencil and asks you to break it, you put your thumbs against the center and bend it. You’d never consider grabbing the two ends and pulling or pushing. You couldn’t even break a toothpick that way.
By sizing the members of a truss just right, you can tune it to carry huge loads while using very little material. This is how people win balsa wood bridge competitions. Real-world trusses can’t be optimized the way a balsa wood bridge can, because real-world trusses have to carry many different combinations of load, and a truss optimized for one set of loads won’t be optimal for another set. Still, even when they can’t be fully optimized, trusses are usually much lighter than alternative structures.
Theory and reality
Speaking of real-world trusses, remember how we defined our ideal truss? Straight members, pinned connections at either end, and loaded only at the joints. Only the first of those conditions is met in a real roof truss. The top and bottom chord members are often continuous though the joints, and the web members are connected through connector plates, not pins.

Furthermore, the top chord is loaded by the roof sheathing along its entire length, not just at the joints.
These deviations from the ideal do, in fact, generate additional stresses by imposing bending loads on the truss members. Fortunately, these additional stresses—structural engineers call them “secondary stresses”—don’t alter the truss’s behavior much and can be ignored in most cases. In trusses, the difference between theory and practice is small.
Uses
So if trusses are strong and stiff and efficient, why aren’t they used for every roof? Three reasons come to mind immediately:
- They take up space in your attic. Although the total volume of lumber used by roof trusses is less than the total volume used by a set of rafters and ceiling joists, the web members of the truss cut the attic up and make it less usable.
- They’re harder to adapt to some roof plans. If your roof has lots of valleys and hips, it’s easier to frame with rafters than with trusses.
- They require extra equipment to put in place. A truss has to be pre-assembled and then lifted as a complete unit up onto the framing. This is no big deal if you’re building an entire subdivision and can hire a crane to do several houses a day. But if you’re just doing a single house, the cost of renting a crane can be prohibitive. Rafters can be put in place by a small crew of framing carpenters.
But trusses are used in lots of roofs, both in residential and commercial construction. Warehouses and warehouse-style stores are almost always use steel trusses because they’re the cheapest way to hold up big, open expanses of roof. Next time you’re in a Costco or Sam’s Club, take a look up.
Postscript: I made the drawings in OmniGraffle and exported them out as PNGs. OmniGraffle’s magnets, auto-alignment tools, and arrows made the job go quickly.
The photo is mine, taken several years ago at a building collapse I was hired to investigate (I’ve done a lot of that over the years). I couldn’t remember the name of the job, but I grep’d for “truss” in my directory of old job reports and soon found the job I was looking for. Flipping through the directory of photos from that job—most of which were of splintered truss pieces, which didn’t seem appropriate—I found what may be the only photo I’ve ever taken of an unbroken roof truss.

