Next post Previous post

Allen Ludden never got cracked

August 26, 2010 at 11:58 PM by Dr. Drang

I followed a link yesterday to this LifeHacker article by John Pozadzides about passwords and how to make yours resistant to hacking. As with most articles of this type, I came away thinking that either the author didn’t really know what he was talking about or decided to dumb things down too much.

Don’t get me wrong; I have no problem with the main points of the articles, which are

  1. Many people choose stupid, easily hacked passwords.
  2. Adding a little length or extending the character set can make a password much more difficult to hack.
  3. Password managers like 1Password (which I use) are a good idea.

It’s the explanation of Point 2 that I have trouble with. Here’s a table from the article (sorry about it being an image instead of an actual table; it’s an image in the original article, too).

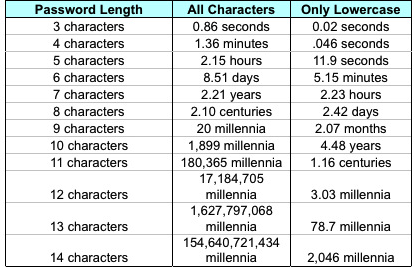
Pozadzides says this is “an estimate of the amount of time it would take to generate every possible combination of passwords for a given number of characters” for an computer of average speed with a “reasonable fast” internet connection. The table is his proof of Point 2, but all it does is confuse me.

I’m not confused by the math; in fact, it’s the simplicity of the math that bothers me. Look at the times in the third column. Note first that the .046 in the second row is a typo—it’s supposed to be 0.46. With that amendment, the durations increase by a factor of 26 with each additional character added to the password length. This is because the number of possible n-character lowercase strings is 26n.

Similarly, the durations in the second column increase by a factor of 95 with each additional character. By “all characters,” Pozadzides means all the printable characters from the ASCII character set, which is everything from character 32 (space) through character 126 (tilde). So the number of possible n-character passwords from this set is 95n.

The change in base means that for a given password length, the duration in column 2 will be

100.563n10^{0.563 n}

times the value in column 3, where 0.563=log(95/26)0.563 = \log(95/26) and nn is the password length. This is not an immediately obvious result, but it’s easy to get if you start by taking the log of the duration ratio

log(95n26n)=n[log(95)−log(26)]=nlog(95/26)\log\left(\frac{95^n}{26^n}\right) = n[\log(95) - \log(26)] = n \log(95/26)

and then “de-logging” by raising 10 to that power.

So all the duration ratios in the table make sense.1 But this doesn’t explain how password cracking programs actually work.

A cracking program trying to hack my GMail account has no idea how long the password is, nor does it know the character set I’m using. Does it start with a dictionary attack? If so, does it try multiple words before moving on to random strings? Does it try lowercase passwords before moving on to the full character set? If so, at what length does it stop trying lowercase passwords? Pozadzides’ simple table doesn’t get into any of these questions, which are a hell of a lot more interesting than raising 26 to a variety of powers.

Suppose, for example, that my GMail password is 5 characters long and that it’s a mix of letters, numbers, and punctuation. According to the table, it would take just over a couple of hours to generate that password. But if the cracking program starts out by generating lists of 3-, 4-, 5-, 6-, 7-, and 8-character lowercase passwords, it’ll be working for over 2½ days on those lists before it even starts making the list that will contain mine. Does that mean a 5-character password with numbers and punctuation is stronger than an 8-character password with only lowercase letters? That isn’t what the table says.

On the other hand, suppose the cracking program generates all the 3-character passwords—lowercase first, then with all characters—then all the 4-character passwords, and so on. In that case, a 6-character lowercase password would be better than a 5-character mixed password. Which isn’t what the table says, either.

Maybe there are no answers to my questions because each password cracker works differently. But I’d like to see an article—pitched to a non-expert audience like me—that at least addresses these issues.

  1. For the duration values themselves, Pozadzides assumes that each password will take one one-millionth of a second to generate, which seems a little slow to me. Also, I don’t understand why he says the speed of the internet connection has anything to do with the speed at which the passwords are generated. The internet connection speed is certainly important when trying out the passwords but not when generating them. ↩

Next post Previous post