Board breaking, part two

September 10, 2010 at 8:17 AM by Dr. Drang

In the first post about breaking boards with karate-like blows, we analyzed when the board breaks (during the initial downward strike, not during the rebound or any subsequent oscillations) and the factors that affect the force delivered during the strike (the momentum of the fist and arm, the duration of the impact, and the shape of the force pulse). Now we’ll analyze the forces and stresses that develop inside the board during the strike and how the wood responds.

Let’s start by assuming the board is lying horizontally between two supports and that a blow from above lands midway between the supports. Under these conditions, which are pretty common, the reaction force at each support is half the impact force. If this result isn’t immediately obvious from the symmetry of the situation, it can be derived by applying Newton’s laws to a free body diagram of the board.

A free body diagram is a conceptual device in which we draw the structure of interest and all the forces that act upon it.

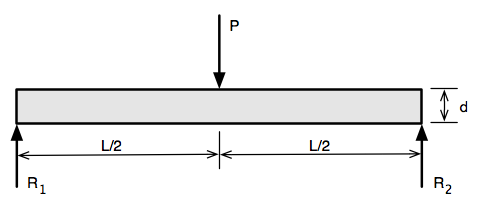
In this free body diagram, we call the impact force $P$ , the distance between the supports $L$ , the depth or thickness of the board $d$ , the width of the board $w$ , and the two reaction forces $R_{1}$ and $R_{2}$ . The reaction forces are determined through:

Vertical equilibrium. The sum of the upward forces must equal the sum of the downward forces. Thus,
$R_{1} + R_{2} = P$
Rotational equilibrium. The sum of the clockwise moments (force × lever arm) about any point must equal the sum of the counterclockwise moments about that same point. Taking moments about the right end of the beam, we get
$R_{1} L = P \frac{L}{2}$

A little algebra leads us to the expected result,

R_{1} = R_{2} = \frac{P}{2}

To determine the internal forces and stresses, we consider just a part of the board, in this case the right half from just beyond the impact force.

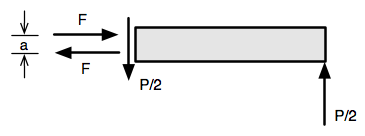
The forces that act on this part of the beam are

The support reaction at the right end.
The internal (vertical) shear force that the left half of the beam exerts on the right half.
The internal (horizontal) tension and compression forces that the left half of the beam exerts on the right half.

From vertical equilibrium, it’s pretty clear that the shear force is $P / 2$ , so I’ve already put that into the free body diagram. From rotational equilibrium, the clockwise moment produced by the two horizontal forces must equal the counterclockwise moment produced by the two vertical forces:

F a = \frac{P}{2} \frac{L}{2}

F = \frac{1}{4} \frac{L}{a} P

What’s $a$ ? It’s the separation between the two horizontal internal forces. We don’t know it’s value yet, but it’s definitely less than $d$ .

Before moving on to figure out $a$ let’s think about what this equation means. First, I’m solving for $F$ because the board starts to break in tension on its bottom surface, and $F$ is the tensile force in the bottom portion of the board. Second, I’ve arranged the equation to show explicitly that $F$ is some multiple of $P$ and that the multiplier is governed by how long and thin the board is. The greater the $L / a$ ratio, the greater the multiplier.

In John Rennie’s article on board breaking, which we discussed last time, he says

When breaking concrete, you use slabs that are relatively narrow and long, so that the strike can hit at a distance from the supports at their edges for best leverage.

The leverage he’s talking about comes from the $L / a$ ratio, and it’s just as true for wooden boards as it is for concrete slabs. When we learned about first-, second-, and third-class levers in school, we were taught to calculate the leverage by taking the ratio of distances from the fulcrum. Here, we don’t have an obvious fulcrum, but leverage is still calculated by taking a ratio of distances.

So back to our question: what is $a$ ? To answer that, we have to know—or make some assumption about—the distribution of stress through the thickness of the board. This is, famously, a problem that Galileo got wrong, believing that stress was a uniform tension through the thickness. Luckily, we can stand on the shoulders of giants and avoid Galileo’s mistake.

The usual assumption is that the tension and compression stresses vary linearly with distance from the mid-height of the beam.

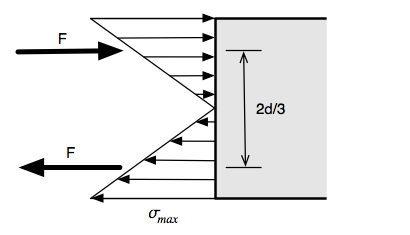
Stress is a force per unit area. Because it has a triangular distribution with depth and is constant with width, the stresses sum to a resultant force like so:

F = \frac{1}{2} σ_{m a x} \frac{d}{2} w

The location of the resultant force is two-thirds the length of the base from the point of the triangle. So

a = \frac{2}{3} d

and therefore

F = \frac{1}{4} \frac{L}{2 / 3 d} P = \frac{3}{8} \frac{L}{d} P

Setting our two expressions for $F$ equal to one another, we get

\frac{1}{4} σ_{m a x} d w = \frac{3}{8} \frac{L}{d} P

From which we see that the maximum tension is

σ_{m a x} = \frac{3}{2} \frac{L}{d} (\frac{P}{d w})

The term in parentheses is the stress we’d induce in the board if we simply grabbed it by the ends tried to pull it apart. For large values of $L / d$ , we get considerable leverage by bending instead of pulling.

It turns out that our assumption of a linear stress distribution, while much better than Galileo’s and quite accurate for over a wide range of loading, isn’t so accurate when the board is close to failure. In most materials, including wood, the distribution looks more like this.

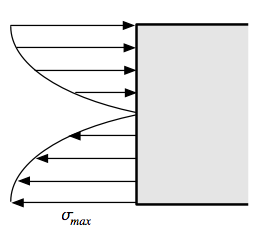
The change in shape doesn’t change the form of the expression for $σ_{m a x}$ , it only changes the leading fraction. If, for example, the stress distribution is parabolic, the formula is

σ_{m a x} = \frac{6}{5} \frac{L}{d} (\frac{P}{d w})

As with the difference between peak load and average load, which we covered in the previous post, this may or may not be an important difference, depending on the precision with which we know the other values in the formula.

So now we understand why we break boards by bending them. Our last topic is the orientation of the grain.

We all know that wood is stronger along the grain than across it. This comes from wood’s microstructure, in which the strong cellulose fibers that run with the grain are held together with weaker lignin. Working with the grain, you have to break the fibers; working across the grain, you only have to break the lignin to separate the fibers.

Carpenters want strength, so they orient wooden beams with the grain running in the span direction from support to support to keep the tension induced by bending ( $F$ ) parallel to the grain. Board breakers have the opposite goal in mind, so they put the grain perpendicular to the span.

How much difference does this make? A huge difference. According to the Wood Handbook, put out by the US Forest Products Service, for pine the tensile strength across the grain is about one-twentieth of the tensile strength with the grain.¹

One last thing about grain: Rennie mentions that board breakers always use pine rather than oak. This seemed odd to me, because I don’t think of oak as being that much stronger than pine. But that’s because I’m used to thinking only of the strength with the grain, for which oak and pine can be relatively close. For example, the Wood Handbook says longleaf pine has a typical along-grain strength of 14,500 psi, which is actually slightly higher than pin oak’s 14,000 psi. Look at the across-grain strength, though, and you’ll see why board breakers prefer pine: longleaf pine has a typical strength of only 470 psi, much lower than pin oak’s 1050 psi.

I started this pair of posts by mentioning my younger son’s recent board breaking triumph. It’s only fitting that I end it with his trophy.

Hi-yaaaah!!

If you look in the Wood Handook tables, compare the “modulus of rupture” values with the “tension perpendicular to grain” values. The modulus of rupture isn’t exactly the same as the tensile strength parallel to the grain, but it’s a fairly close estimate, and it’s intended to be used to determine bending strength. ↩

And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Board breaking, part two

Site search

Meta

Recent posts

Credits

And now it’s all this

I just said what I said and it was wrong Or was taken wrong

Board breaking, part two

Site search

Meta

Recent posts

Credits

I just said what I said and it was wrong
Or was taken wrong