Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

Problem 31

The first thing to notice in this problem is that the two arms of the toggle are two-force members (which you may recall from Problem 23), so the forces transmitted by those arms must be aligned with them. We draw the free-body-diagram of the rolling block at the right end of the toggle like this

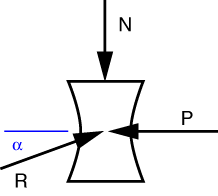
The horizontal equilibrium equation is

\sum F_x = R \cos \alpha - P = 0

which tells us that R = P/\cos\alpha. We can now draw an FBD of the hinge at the center of the toggle

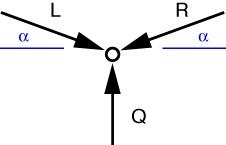
The equilibrium equations for the hinge are

\sum F_x = L \cos\alpha - R \cos\alpha = 0

and

\sum F_y = Q - L \sin\alpha - R \sin\alpha = 0

From the first of these, and our previous solution, we see that L = R = P/\cos\alpha. Plugging this into the second equation gives us

Q = \frac{P}{\cos\alpha}\sin\alpha + \frac{P}{\cos\alpha}\sin\alpha = 2 P \tan\alpha

which is the solution at the back of the book. Notice that for small angles, Q will be much less than P. Since toggles like this are usually set up with Q as the applied force and P as the resistance, you can see how this mechanism is a great force multiplier.

Problem 32Problem 30

Last modified: January 22, 2009 at 8:32 PM.