Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

Problem 39

Let’s start with a free-body diagram of the block of ice.

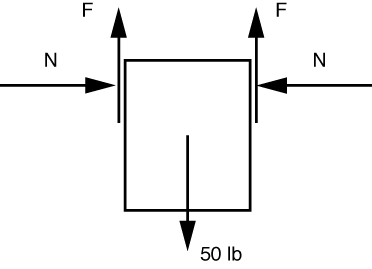
We’ve used symmetry to recognize that the forces on either side of the block must be equal. The vertical equilibrium equation is

\sum F_x = 2 F - 50 = 0

and the solution is F = 25 lbs.

The FBD of one of the tong bars is

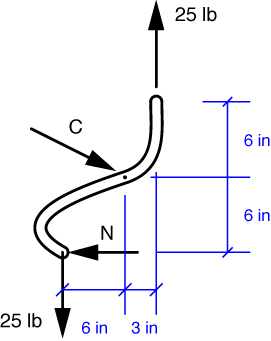
Moment equilibrium about the pin C gives

\sum M_C = 25 \cdot 3 + 25 \cdot 6 - 6 N = 0

The solution of this equation is N = 37.5 lbs, which is the answer to part a). Vertical equilibrium tells us that the vertical component of the force at C is zero, so it should be drawn as a purely horizontal force. Horizontal equilibrium tells us that C = 37.5 lbs, which is the answer to part b)

The Eugene O’Neill reference that starts off the problem statement is one of those little quirks that places the book in the post-war years.

Problem 40Problem 38

Last modified: January 22, 2009 at 8:32 PM.