Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

Problem 48

The next five problems are pretty similar, and we’ll be using similar techniques to solve them. The solutions will rely on:

  1. Static equivalence, in which we will replace certain applied loads with other loads that have the same resultant. The support reactions that come from the application of a statically equivalent set of loads are the same as the support reactions that come from the original loads.
  2. Superposition, which is the principle that the effect on a structure of a set of several loads is the same a sum of the effects of the individual loads.

Our first step will be to replace the non-pin loads with a set of pin loads that have the same resultant (that are statically equivalent). The free-body diagram will be this.

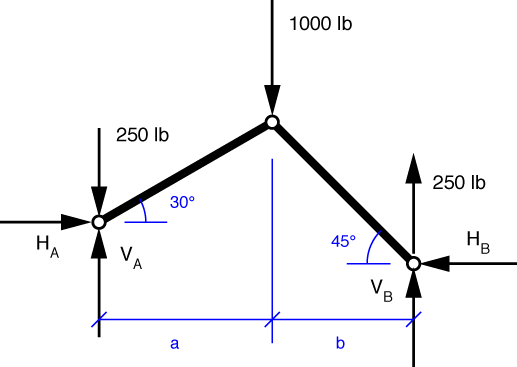
Each 500 lb load at the center of a bar has been replaced with two 250 lb loads at the pins at the ends of the bars. The downward 250 lbs from the left bar and the upward 250 lbs from the right bar cancel each other at the top pin. This solution to this problem can be found by adding the solutions of this problem

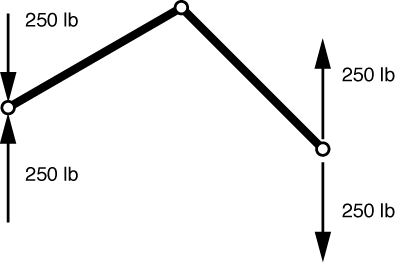
(which is so trivial I’ve just put the solution in the FBD) and this problem

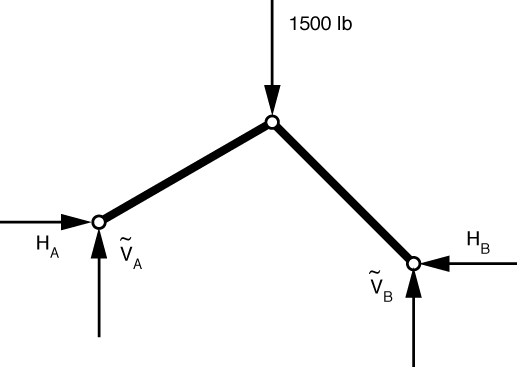
In this second sub-problem each bar is a two-force member, so the relationships between the horizontal and vertical components is known:

\frac{\tilde {V}_A}{H_A} = \tan 30^\circ, \frac{\tilde {V}_B}{H_B} = \tan 45^\circ

The FBD of the top pin is

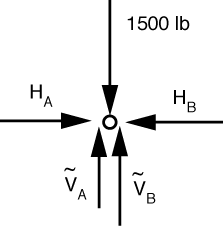
Horizontal equilibrium tells us that H_A = H_B = H and vertical equilibrium says

1000 = \tilde {V}_A + \tilde {V}_B = H \tan 30^\circ + H \tan 45^\circ

Solving for H gives us H = 634 lbs, and therefore \tilde {V}_A = 366\,\rm{lbs} and \tilde {V}_B = 634\,\rm{lbs}. Adding in the results of the first sub-problem to the results of the second gives us

H_A = H_B = 634\,\rm{lbs}
V_A = 366 + 250 = 616\,\rm{lbs}
V_B = 634 - 250 = 384\,\rm{lbs}

which matches the answer in the back of the book.

Problem 49Problem 47

Last modified: January 22, 2009 at 8:32 PM.