Friction
June 30, 2011 at 9:30 AM by Dr. Drang
I stopped into one of the few remaining Borders stores in the area the other day, mainly to see whether the insides looked more like a bookstore or a fire sale. I ended up buying a book and relearning what a picky pain in the ass I am.
I saw the book The Way We Work on the bargain shelves as I headed toward the science and computer aisles near the rear of the store.

It’s a book about the human body by David Macaulay, the guy who wrote Pyramid, Castle, Cathedral, and The Way Things Work. TWTW was probably his most popular book and that, no doubt, was the reason this book used it as the inspiration for the title.
Two thoughts immediately crossed my mind:
- I should get this for my younger son.
- I wonder if Macaulay ever fixed that friction mistake in TWTW?
The first thought was resolved by buying the book (after first checking that Amazon’s price was higher).
The second thought requires some explanation. I loved Macaulay’s early books on buildings, and when TWTW came out in 1988 I bought the hardcover right away.

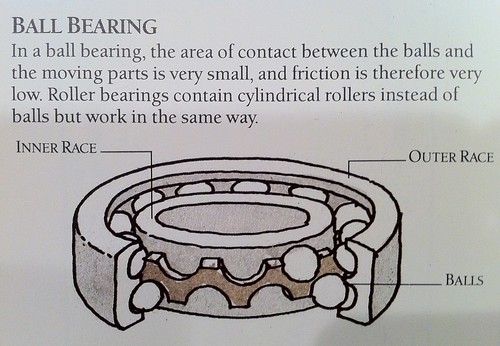
I was teaching back then, so in addition to just appreciating Macaulay’s work, I thought I might pick up some ideas for explaining things in the classroom. I’m not sure I ever used any of his descriptions in my classes, but I did find one explanation to avoid: his description of ball bearings.
In a ball bearing, the area of contact between the balls and the moving parts is very small, and friction is therefore very low. Roller bearings contain cylindrical rollers instead of balls but work in the same way.
No no no no no no no!
Friction does not depend on the contact area, and ball bearings don’t work because the friction between the balls and the races is low. Ball bearing work because the balls roll on the inner and outer races, and rolling actually depends on friction.
Let’s look at a section of the races with just one ball. If the friction between the ball and races is sufficiently high, the surface of the ball won’t slip against either the inner or the outer race; it’ll simply roll along each of them. Since frictional energy losses come about when parts slide against one another, the design of the bearing avoids these energy losses by avoiding slip. Ironically, high friction between the balls and the races helps avoid frictional energy loss.
It isn’t a perpetual motion machine because the design doesn’t avoid all energy losses. There are still frictional losses because the balls slide against the cage (that’s the brownish thing separating the balls in Macaulay’s drawing). There’s also energy lost in the deformation of the balls and the race and in any rattling around the balls may do because of surface roughness or poor fit. But with hard, smooth parts, tight tolerances, and good lubrication of the cage, these losses are very small. Which is, of course, the reason people make and use this type of bearing.
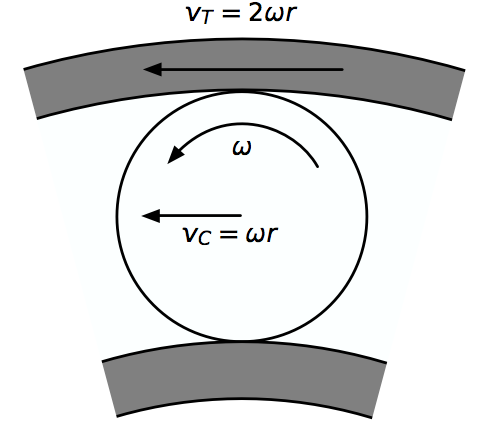
As a no-cost bonus for reading the blog today, I’ll throw in a little kinematics. Let’s call the radius of the ball and its angular speed . We’ll assume that the inner race is stationary (this isn’t necessary, but it makes the analysis easier) and that the balls roll without slipping along the two races.
We can then say:
- The point on the ball that contacts the inner race has a velocity of zero because the inner race is stationary and there’s no slip between the inner race and the point on the ball in contact with it.
- The tangential velocity of the center of the ball is .
- The tangential velocity of the point on the ball in contact with the outer race is .
- The tangential velocity of the outer race is also because there’s no slip between the outer race and the point on the ball in contact with it.
That means the outer race goes around the inner race twice as fast as the balls do, which is kind of neat.
OK, let’s get back to friction and me being a pain in the ass. So Macaulay made this mistake in the first edition of the book. Almost a quarter of a century later, when I see another book by Macaulay, the first thing I think of is this mistake. I wish I weren’t that way, but there you are.
Even worse, when I was in a library a few days later, I found a later edition of the book—now called The New Way Things Work—and looked to see if the mistake had been corrected. It hadn’t; the drawing and the text are exactly the same as in the first edition.
So not only do I have to live with the knowledge that I’m such a nitpicker I couldn’t forget a solitary mistake in an otherwise wonderful book written by a man who’s made many wonderful books, but I also feel guilty for not writing to the author and explaining the mistake so he could fix it.