A Talk Show pair
February 25, 2025 at 4:37 PM by Dr. Drang
I listened to the most recent (and long-delayed) episode of The Talk Show today as I drove south from home to Champaign-Urbana to watch the Illini men’s basketball team try to reclaim their season against the Iowa Hawkeyes. The drive usually takes between 2 and 2½ hours, which is a perfect length for The Talk Show.
While discussing the new iPhone 16e, John Gruber and guest Paul Kafasis lamented the phone’s lack of MagSafe charging and speculated on why Apple left it out. I would say “money,” but that might be too generic of an answer. In any event, John and Paul agreed that they’d never buy an iPhone without MagSafe.
This struck me as odd. I’ve never been a particular fan of “wireless” charging. I don’t know why I’d want to spend more for a puck that recharges my phone in a less efficient way than plugging in. Especially since the puck is just as tethered to an electrical outlet as a standard USB-C cord. Now, when charging becomes truly wireless, and my phone can top itself off as a I walk around with it in my pocket, then I’ll be happy to pony up for that kind of charging station. But until then, I’m not wasting my money.
This feeling of superiority shrunk as I looked down to see my phone sitting on its back in the tray of my car’s center console. The tray that has a Qi charger under it and recharges my phone so conveniently as I drive around. I can make a decent argument that this isn’t really like a puck—it came with the car; I didn’t pay extra for it—but there’s no question that I am using wireless charging and it’s very nice. I should be more tolerant of MagSafe fans.
Later in the show, as they were discussing Rogue Amoeba’s recent escape from sandbox hell, John and Paul talked about how OS X/macOS has changed over the past couple of decades and what’s lost when an operating system’s emphasis shifts from ease of development (which has benefits for users as well as developers) to user safety.
This discussion came back to me as I walked around campus and found it difficult to get into some buildings—buildings that were almost always open to everyone who came along back when I was a student here. This isn’t new to me, and it isn’t true of most buildings, at least not during normal classroom hours. But you need credentials to get into some places during the day and most places in the evening. The shift in emphasis from campus openness to campus safety parallels what we see in the Mac. And as with the Mac, something has been lost with this shift. I’m not saying it isn’t the right choice. There’s no particular reason 64-year-old alumni should be able go wherever they like. But there’s definitely a different feel.
Apple’s weather direction
February 23, 2025 at 4:17 PM by Dr. Drang
Back in January, I got a question from Adam Bodnar on Mastodon:1
With the new macOS weather menu bar, can you explain what the blue line is indicating here?
I assume that it’s saying that it’s going to feel colder as the day goes along?
At the time, I hadn’t fiddled enough with Control Center to put Weather into my menu bar, so I wasn’t sure how to answer Adam. But a day or so later, I saw a similar graphic in iOS. It’s not one of Apple’s better attempts at graphical communication. And now that I’ve added Weather to my menu bar, I’d like to address it.
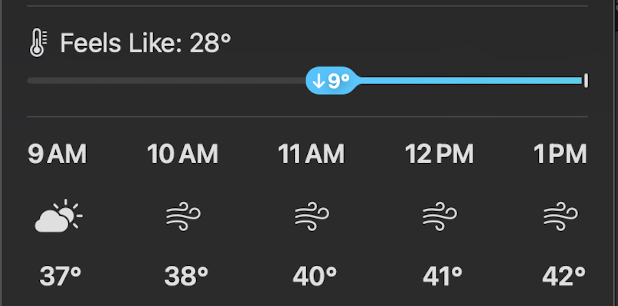
Here’s what Weather looked like earlier today on my MacBook Pro.
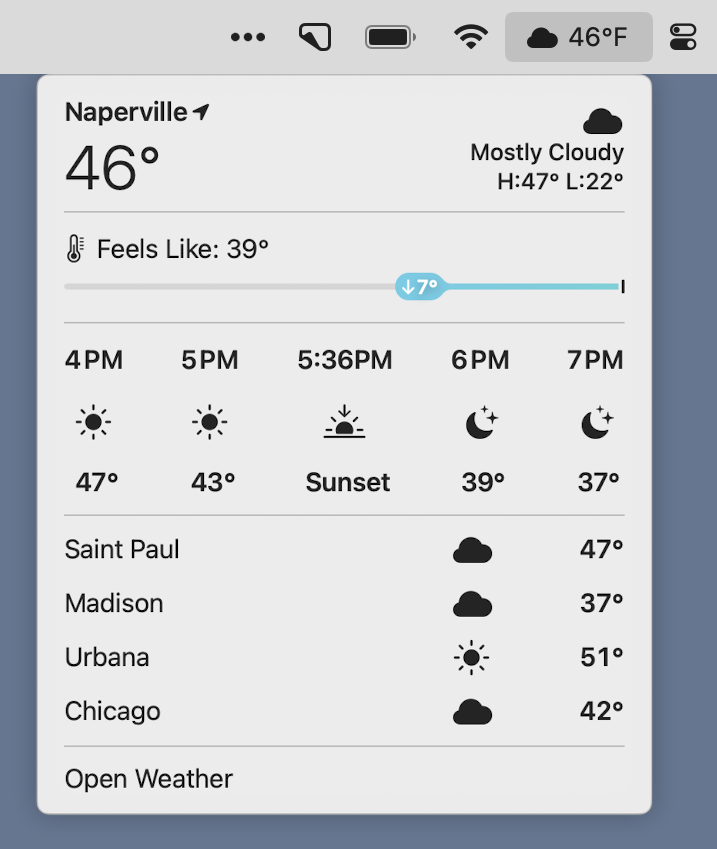
As you can see, I don’t use Dark Mode, but otherwise, the middle section of this screenshot is basically the same as what Adam was wondering about. What’s going on here is that Apple is using the blue line to emphasize the drop in “feels like” temperature due to wind chill. The graphic is redundant, because the two temperatures above it already show us that the wind chill is 7° below the actual temperature. But the redundancy isn’t what’s wrong with the graphic—having two ways of showing the same thing can often be helpful. What’s wrong is its placement and sense of direction.
The blue line is acting like a number line, and the little oval is meant to show us how far below the real temperature the “feels like” temperature is. Going left on a number line means going to a smaller number. Why that particular distance represents 7° is beyond me. Unlike the number lines you saw in grade school, this one has no scale.2
The more serious problem with the blue line is that it sits immediately above the timeline of temperatures and weather conditions, and it takes up the same horizontal space. This is what led to Adam’s confusion. At first glance—and a lot of graphical communication is about first glance—the blue line seems to have something to do with the next few hours.
It looks like Apple recognized the potential for confusion, but did a poor job of dediscombobulation. Tucked into the little oval with the 7° is a downward arrow. Because down means a reduction, right? Except we’ve already established that left means a reduction. And right means later in the day. The clarity is almost painful.
I assume that as we move into summer (going to the right), the blue line will change to red and it will start from the left edge to show us how much hotter it feels because of humidity. And there’ll be an upward arrow in the oval because Apple’s afraid we won’t understand that right means increase. Right?
-
I meant to link directly to Adam’s toot, but his account is locked. I hope he doesn’t mind this small quotation. ↩
-
You may remember Bezos Charts. ↩
Siri and license plates
February 21, 2025 at 3:49 PM by Dr. Drang
This morning, I went to Swallow Cliff Woods to walk around its trails. As I was driving there and listening to a podcast through CarPlay, an Amber Alert icon appeared on the screen. When I tapped the screen, Siri described a car I was to report if I saw it. There were a couple of weird things about the alert.
First, although this happened a little after 8:00, I later learned that the alert had been canceled more than three hours earlier. So not particularly timely.
Second, the way Siri gave the license plate number of the car was not the way any person would say it. It made me think about Siri rather than the car I should have been looking for (if I’d been driving around four hours earlier). The license plate number was DK97105 and Siri pronounced it
Dee-kay, ninety-seven thousand, one hundred, five
as if it were an actual number, rather than just a string of identifying digits. It was so strange I didn’t really hear anything after “ninety-seven thousand.” I looked it up in notifications before starting this post.
If the string of digits were shorter, a person probably would say them as a number. DK97 would come out as “dee-kay, ninety-seven.” DK971 might be “dee-kay, nine seventy-one,” where you’d think of it as “nine hundred, seventy-one,” but you wouldn’t say the “hundred.” Four-digit numbers would probably come out as a pair of two-digit numbers, with DK9710 being pronounced “dee-kay, ninety-seven, ten.”
I wouldn’t expect Siri to do this, though. The variations from person to person are too great to trust an algorithm to come out with something that sounds natural. The safest solution is for numbers that represent quantities to be pronounced as numbers, and numbers that are merely ID codes to be pronounced as a series of digits—in this case, “dee-kay, nine seven one zero five.”
As is often the case, Siri’s mistake comes from not recognizing context. Apple has given Siri the ability to recognize phone numbers—if you include parentheses or hyphens—and it pronounces them digit-by-digit. But even though the phrase “license plate” was in the alert, Siri treated it as a quantity. Dumb.
Chit chat about charts
February 10, 2025 at 9:06 AM by Dr. Drang
Speaking of Jason Snell, which I was in yesterday’s post, he recently gave an interesting interview to Allison Sheridan on her Chit Chat Across the Pond podcast. The topic was Jason’s longstanding series of charts following Apple’s quarterly results—the latest of which is here—and a few things stood out to me.
First, while I knew that Jason used Numbers to make his charts, I didn’t know how he pulled those charts out of Numbers to post on Six Colors. I guess I thought he copied them by right-clicking and saved them as PNG files using AppleScript or Automator or Shortcuts. But no. He has all his charts laid out on a single tab in Numbers, saves that tab as a PDF, and then has a script that extracts rectangles from the PDF, one for each chart, and saves those as individual PNGs. More automated than I would’ve thought possible when using Numbers. (Yes, I had forgotten that Jason wrote about this several years ago.)
I was happy to hear, though, that Jason’s charts are not fully automated. He still tweaks his graphs by hand when necessary to get them to look right. To me this is a sign of care. It’s virtually impossible to set up a graphing template that always produces good looking charts for every set of data that comes down the pike. Experienced graph makers give themselves the leeway to change settings to meet the needs of new data.
Finally, I was surprised to hear that Jason’s data table, which he updates by hand whenever a new earnings report comes out, puts each quarter in its own column and all the categories—like Mac, iPhone, and iPad sales—in rows. This is a violation of table orthodoxy, in which fields are columns and records are rows. This standard method of organization is, of course, arbitrary, but software tools that deal with tables assume that they’ll be laid out this way.1
But Jason doesn’t use software tools like R or Pandas to build his charts, so he can organize his table as he sees fit. And after thinking about it for bit, I realized why this transposed table would be easier for him to work with. Here’s an excerpt from the most recent Apple earnings report:
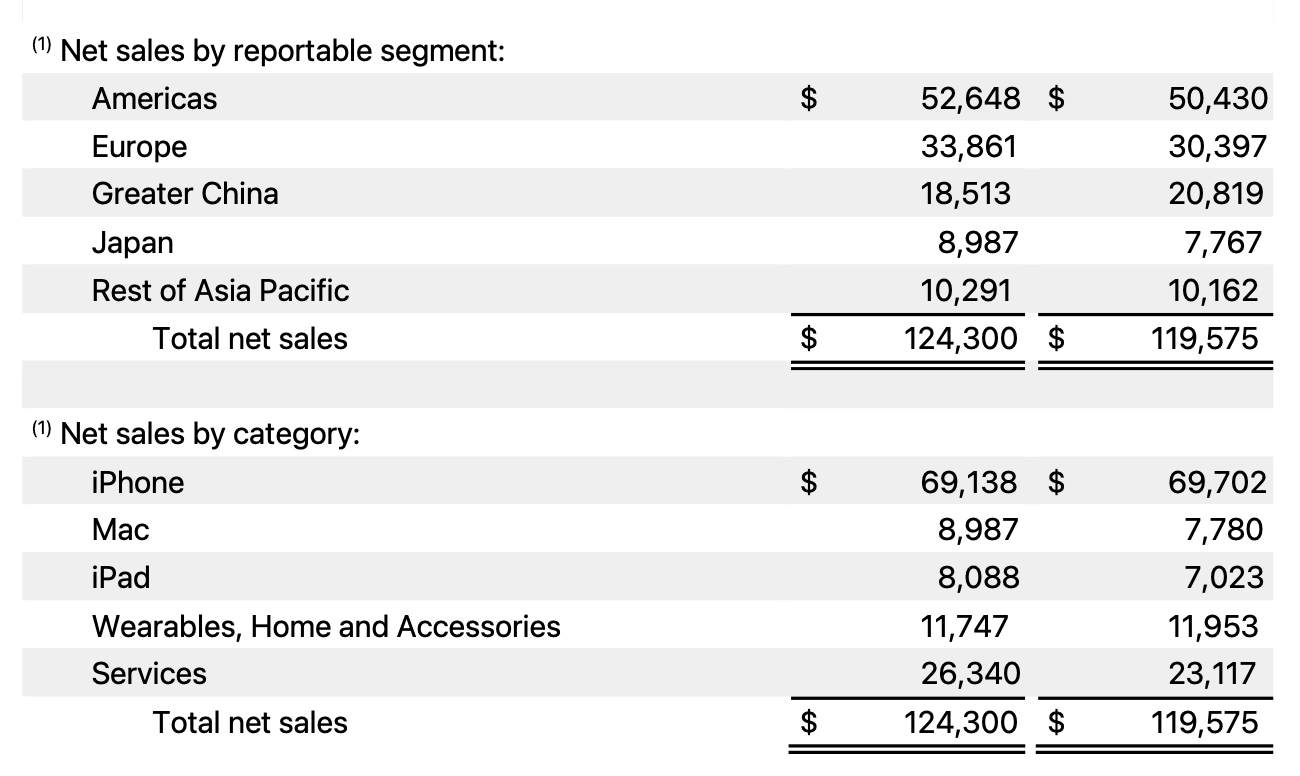
The figures for the current quarter and the year-ago quarter are in columns and the categories are in rows. By having his Numbers table organized this same way, Jason can type in the values the way he sees them in the report. It’s much easier to proofread this way. Also, he can quickly look back a few columns to make sure his data for the year-ago quarter matches Apple’s. Affordances like this are invaluable when entering data by hand.2
Even though I’m wedded to using Python (and sometimes Mathematica) for graphing, it’s alway good to hear how people use other tools. Thanks to Allison and Jason for some topics to chew on the next time I want to make a few charts.
-
The orthodoxy is not entirely arbitrary. Tables tend to grow to have more records than fields, and it’s easier to lay out a long table on paper than a wide one. ↩
-
Many many years ago, I had to copy dozens of pages of numbers from a faded printout into a spreadsheet. OCR was out of the question. I made a paper template with cutouts so I could keep my eyes aligned and copy only the columns of interest. It was tedious, but it worked. ↩