A tardy assessment of the Apple Sports app
April 12, 2024 at 1:00 PM by Dr. Drang
I tried the Apple Sports app when it came out in February and abandoned it almost immediately. Lots was written about Sports in its first couple of weeks, but I was on a blogging hiatus back then. I’ve recently looked at it again to see if I was too hasty or if its failings had been fixed (no to both), so I figured I’d write up my thoughts.
I won’t be saying anything about how Sports fits into the Apple sports universe; go to Jason Snell for that. And I won’t be talking about how its design may be a harbinger of iOS 18; that’s Lickability’s baliwick. But I do want to talk about its design as a sports app.
You may recall that the main selling point of Sports was its ability to give you up-to-date scores. Eddy Cue said, “I just want to get the damn score of the game.” That’s Apple marketing at its best: it’s short, pithy, and it directs you to the app’s best feature, the presentation of today’s scores.
It’s easy to set up Sports to follow your favorite leagues/conferences and teams, and once that’s done the presentation of scores is logical. Games being played in your chosen leagues are displayed generally in chronological order, but the games with your favorite teams are floated to the top. That’s the right way to do it.
But scores are only part of what a good sports app is about. Sports apps are used not only when you can’t watch a game and want to be kept plugged in, they’re also used—even more often used, I think—to give you background information on the game you’re currently watching. Announcements during a broadcast are ephemeral, but a sports app can tell you how many fouls Nikola Jokić has at any time.1 And this is where Sports falls down.
In basketball, for example, the box score statistics are thin. There’s no info on free throws, steals, blocks, turnovers, or personal fouls. League standings are missing common stats like the home/away record, record over the last 10 games, and win/loss streaks, These are things fans want and that other sports apps provide. No amount of beautiful presentation is going to make up for missing data.
And, weirdly for an Apple app, the presentation isn’t beautiful—it’s actually awful. Here’s a screenshot of the box score from last night’s Chicago Bulls/Detroit Pistons game:
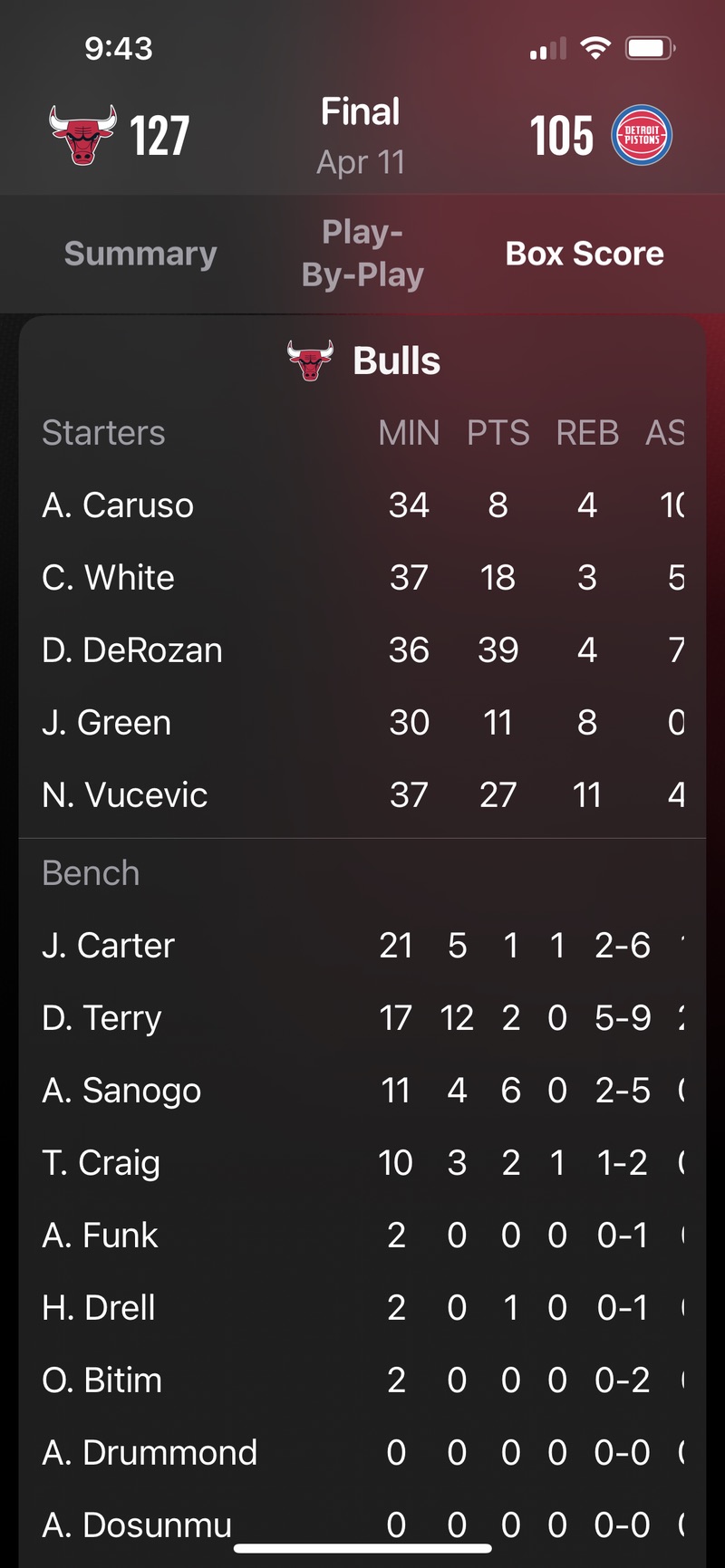
Like many sports apps, Sports splits the box score into starters and bench players (during a game, the players on the court have marks next to their names). Apple’s designers decided to put the headers only at the top of the Starters portion of the table, which I would applaud if they’d aligned the columns of the Bench portion of the table with the columns of the Starters portion. But they didn’t. Bench rebounds, for example, are more or less under the PTS header. This is not how you present a table of numbers, and it’s inconceivable to me that anyone would look at this mess and give it a pass.
The programming problem here is obvious. Although the use of a single header suggests this is meant to be seen as a single table, inside the app the Starters and Bench parts are two separate tables. The column spacing of the Starters table is based on widths that include the headers (several of which are wider than the data below them), and the column spacing of the Bench table is based on widths of the data alone. Instead of looking at both tables, getting the maximum width of each column, and applying that to both tables, the programmers simply allowed the tables to be formatted separately, thus saving themselves at least five lines of code.
Again, did nobody at Apple look at this before putting it in the App Store? And has nobody looked at it in the seven weeks since?
I admit I may be unduly irritated by this because I spent a lot of my career making tables of figures and doing my best to make them easy to read. But before you dismiss me as a crank, look at what happens when you swipe on the tables left and right to see the additional stats. They get even further misaligned because the two tables don’t scroll together.
When you use a single header, you’re telling the reader that they’re looking at a single table. But this design cheats the reader.
I’ve used several sports apps over the years. Many of them are crappy and fill your small screen with ads. A good Apple Sports app would fill a real need. But I can’t use it until it stops offending me.
-
My examples are going to be about basketball because that’s the sport I care about the most. ↩
Counting poker hands
April 11, 2024 at 12:13 PM by Dr. Drang
In this morning’s blog post, John D. Cook talks about poker hands and their probabilities. In particular, he says
For a five-card hand, the probabilities of 0, 1, or 2 pair are 0.5012, 0.4226, and 0.0475 respectively.
Upon reading this, I assumed there’d be an explanation of how these probabilities were calculated. But no, he just leaves us hanging. So I sat down and worked them out.
The probabilities are going to be calculated by dividing the number of ways we can get a certain type of hand by the total number of possible hands. So let’s start by working out the denominator. There are 52 cards, so if we deal out 5 cards, there are
possible ways to do it. The symbol that looks sort of like a fraction without the dividing line represents the binomial coefficient,
This is not only the coefficient of binomial expansions, it’s also the number of ways we can choose k items out of n without regard to order, also referred to as the number of combinations.
To figure out the number of one-pair hands, imagine the deck laid out in 13 piles: a pile of aces, a pile of kings, a pile of queens, and so on. We then do the following:
- Pick one of the piles. There are 13 ways to do this.
From that pile, choose 2 cards. There are
ways to do this.
Pick three other piles. There are
ways to do this.
- Pick one card from each of these three piles. Since there are 4 cards in each pile, there are ways to do this.
So the total number of one-pair hands is
and the probability of getting a one-pair hand is
Moving on to two-pair hands, we start with the same 13 piles we had before. We then do the following:
Pick two of the piles:
Pick two cards from each of these piles:
- At this point, any of the remaining 44 cards will give us a two-pair hand.
Therefore, the total is
and the probability of drawing a two-pair hand is
Counting the number of no-pair hands is a little trickier because we have to make sure we don’t mistakenly count better hands, i.e., straights and flushes. Starting again with our 13 piles, we do the following:
Pick 5 piles
Eliminate all the straights from this number. The number of straights is most easily done through simple enumeration:
A–5, 2–6, 3–7, 4–8, 5–9, 6–10, 7–J, 8–Q, 9–K, 10–A
So 10 of our 1,287 possible pile selections will give us a straight. That leaves 1,277 non-straight possibilities.
- Pick one card from each of the selected piles. That gives possibilities.
- Eliminate the flushes from this set of possibilites. There are 4 flushes, leaving 1,020 possibilities.
These steps give us
hands that are worse than one-pair. The probability of getting such a hand is
I kept one more digit in my answers than John did, but they all match.
My 2024 Eclipse
April 9, 2024 at 7:47 PM by Dr. Drang
I drove down to Vincennes, Indiana, yesterday to see the eclipse, and everything was just about perfect—some through planning and some through serendipity. Here’s a brief review.
Vincennes was not my first choice. Using the eclipse path map at Time and Date, I looked for the shortest distance from Naperville, Illinois, to the path and figured I’d shoot for a rural area near Indianapolis.
As Eclipse Day got closer, I began to have second thoughts. Two reasons:
- Traffic before and after the 2017 eclipse—which I saw with my wife and sons in southern Illinois—was a nightmare. Going near a decent-sized city ringed by a set of interstate highways seemed like a bad idea.
- Weather reports for the Indianapolis area were a little sketchy. Apple’s Weather app said it would be cloudy in the morning turning to partly cloudy by the time of the eclipse. “Partly cloudy” covers a wide range of cloud cover. Various weather websites also predicted partly cloudy skies, with less cloud cover as you moved southeast along the eclipse path.
So I started looking into Vincennes. It’s about an hour farther than Indianapolis under normal driving conditions, but I could get there via state and US highways instead of interstates, so I figured it was unlikely to attract as many people as the Indianapolis area. And it was supposedly less likely to have clouds.
Ultimately, it was a game-day decision. When I woke up on Monday morning and looked at the forecasts for Indianapolis and Vincennes, Vincennes seemed like it would have slightly better weather. And when I left, sometime between 5:30 and 6:00 in the morning, my route to Vincennes showed no delays. I didn’t truly trust the traffic because I wouldn’t expect people to be crowding the roads until I was two or three hours into my trip.
The drive went very well. I worked my way south and east to US 41 in Indiana (it became an hour later when I crossed the state line) and headed south. As I headed down through the land of windmills, Trump signs, and dollar stores, the traffic was light and the sun was bright. Somewhere—I think it was a bit north of Terre Haute—there was a billboard encouraging everyone to go to Vincennes for the eclipse, but there didn’t seem to be that many people following its directions.
I rolled into Vincennes around 11:30, desperate to use a bathroom. I stopped at a McDonalds and then felt obligated to eat there after using the facilities. Here’s where the serendipity struck. As I was eating (worst fries I’ve ever had at a McDonalds—remind me to tell you about the glorious fries I once had at Hamburger University), I started looking on my iPhone for a park nearby where I could kill some time before the eclipse, which wouldn’t get started for over two hours.
A website describing Kimmel Park on the north side of town, right along the Wabash River, said it had 1.8 miles of walkways. This appealed to me, as I’d missed my morning walk. For no particular reason, I opened the eclipse path page at Time and Date and zoomed in as far as I could. The centerline of the path went right through Kimmel Park.
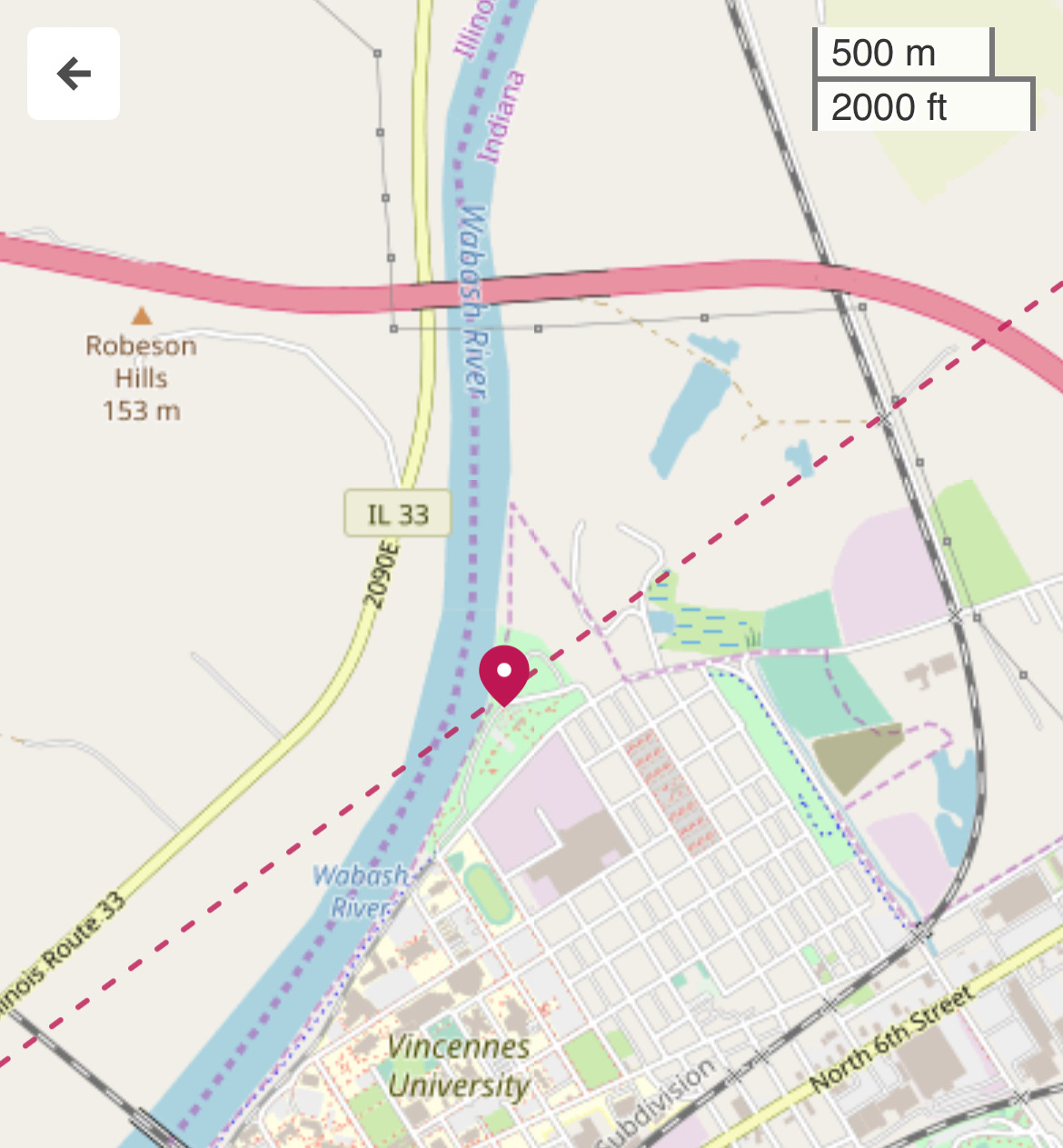
You see, I had not been planning to stay in Vincennes for the eclipse. It had looked to me as though the path went north of town (which it kind of does), so I was going to find a spot alongside a county road north and east of town, between Vincennes and Bruceville, for watching the eclipse. But now I had a better place, assuming the park wasn’t overrun with visitors.
It wasn’t. There were well-marked lots with free parking and mostly empty spots near the park. And while the park was far from empty, it wasn’t hard to find a place to settle in after I’d walked around it once. (While I’m sure the “1.8 miles of walkway” is accurate, that must be if you take every last branch, possibly doubling back on yourself.)
Here’s where I parked and where I sat for the eclipse.
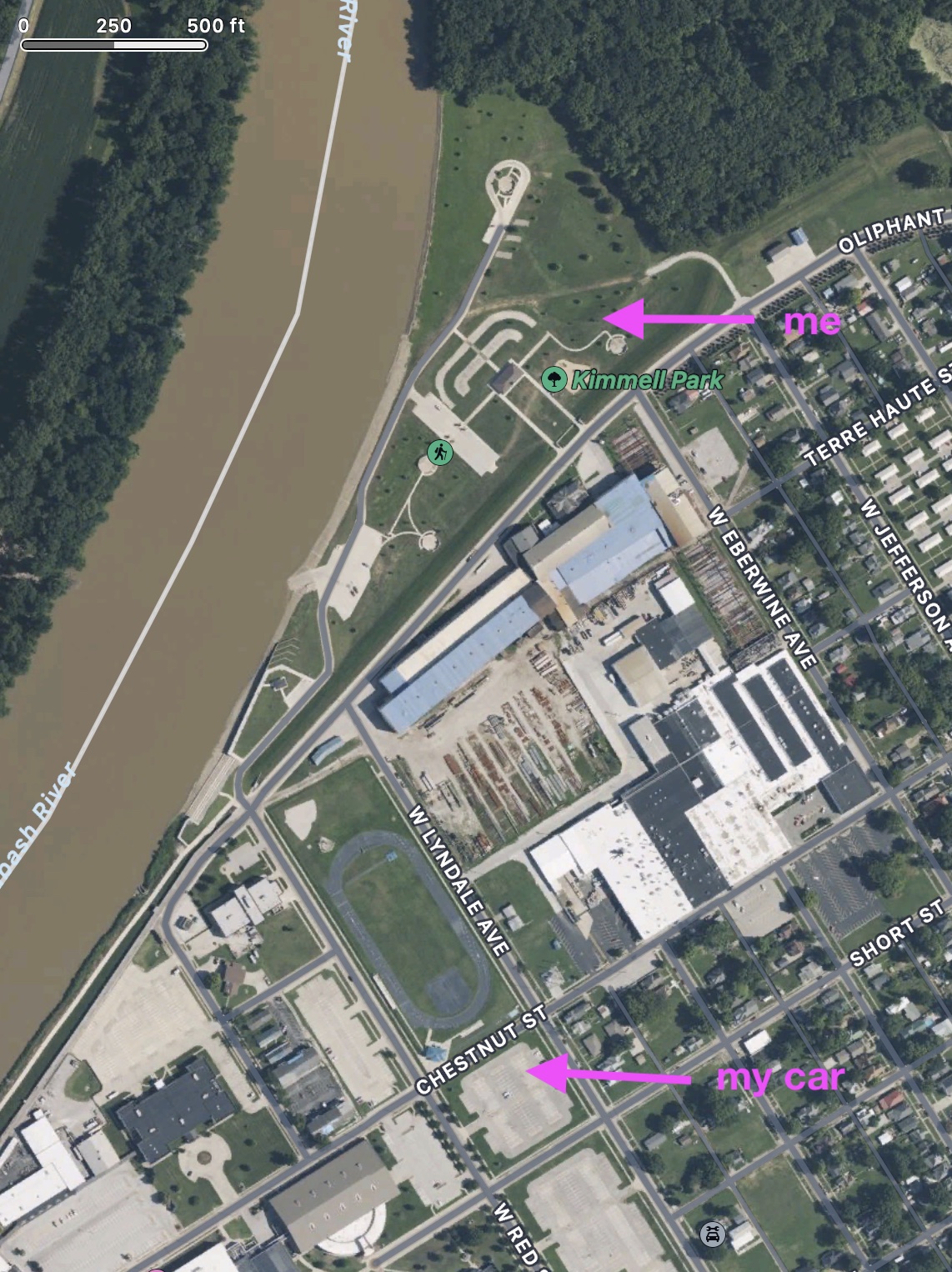
I used the location data for a photo I took to mark the exact location.

Honestly, I think I was at the next tree north and east of where my photo said I was, but I don’t want to argue with GPS.
How does this compare with the centerline of the eclipse path? This morning, I opened Mathematica and used its new SolarEclipse function to mark the path on map that’s more zoomed-in than I could get with Time and Date:
eclipse = SolarEclipse[DateObject[{2024, 4, 8}]];
GeoGraphics[{Red,
SolarEclipse[eclipse, "ShadowAxisLine"],},
GeoCenter -> GeoPosition[{38.69715, -87.51673}],
GeoRange -> Quantity[250, "Meters"], GeoScaleBar -> "Feet",
ImageSize -> Large]
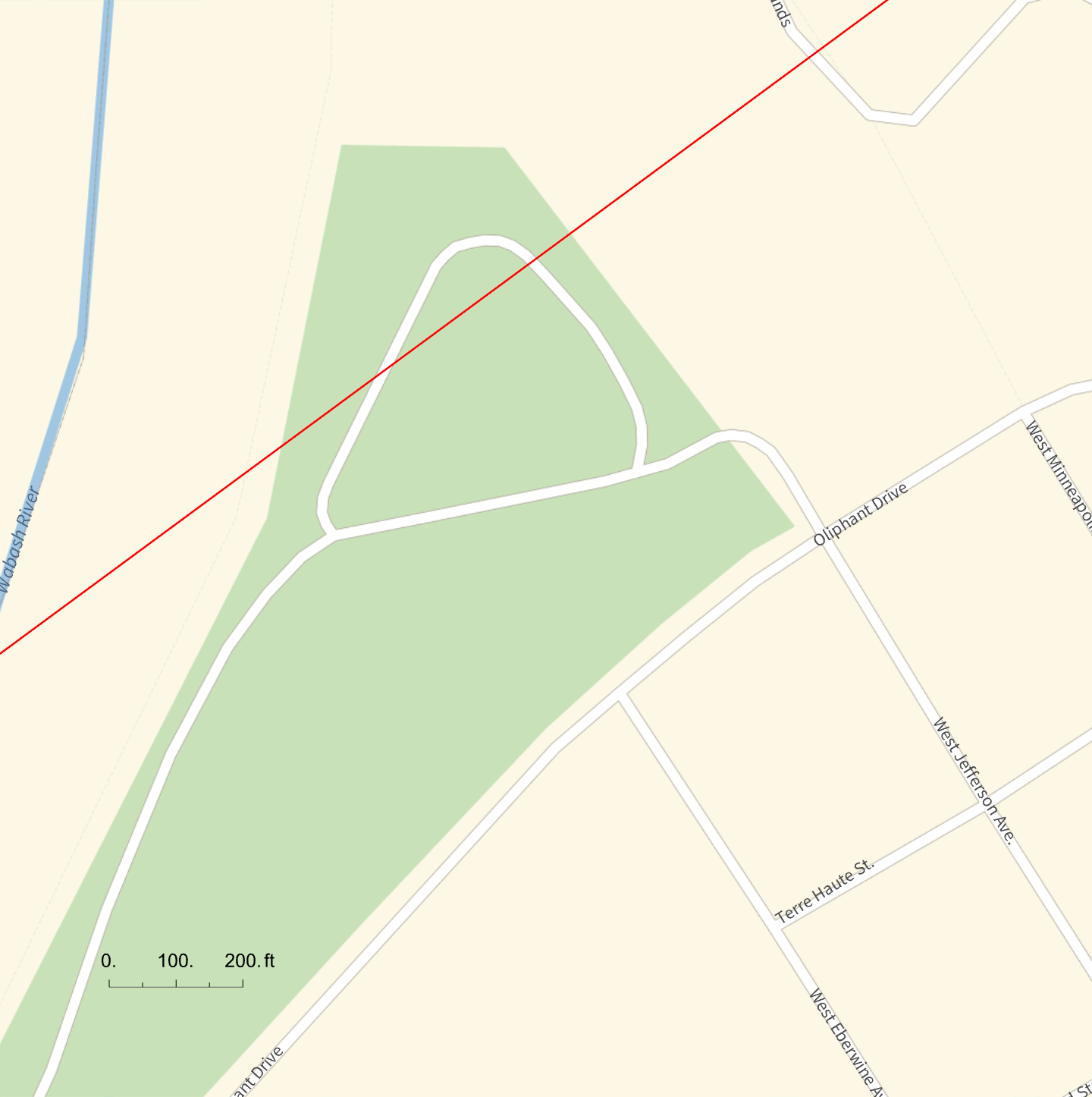
Apparently, the park district has changed the routing of the paved areas, but you can see that I was no more that 300–400 feet from the centerline. Recent rains had left the ground and some of the pavement wet by the peak of the triangle, and the shady areas near the treeline due north of me was already occupied. So I was satisfied with my spot.
There were some thin, wispy clouds, but it was obvious well before the eclipse started that the view would be fantastic. And it was. During the last 10–15 minutes or so before totality, I did nothing but look at the sun (through the glasses I’d kept from 2017), watching as the thin arc of sun got shorter until it disappeared entirely. I pulled off my glasses as a cheer went up and looked into the deep black of the moon surrounded by the white corona.
I did take a quick iPhone photo during totality, more as a reminder than anything else.

Patrick MaCarron—who was also in Vincennes, but I don’t know where—took a great photo of the eclipse, and you should follow the link to see it. It shows two red prominences: a large one near the bottom and a smaller one along the right edge. I saw the one near the bottom with my naked eye; it was a sharp red dot at the bottom of the black circle. I was unsure if I’d really seen it until I saw Patrick’s photo later on Mastodon.
I also found Jupiter (to the right) and Venus (to the left). I didn’t see Mars, Mercury, or that comet that was supposed to be at the edge of unaided visibility. This, I think, is where those wispy clouds came into play. I could see them around Jupiter, sort of how you see clouds on a moonlit night.
I hung around for a while after totality, but watching the Moon retreat isn’t as fun as watching it advance. As I walked back to the park entrance, I stopped to take photos of my shadow on the sidewalk. I made a sort of pinhole by squeezing tight an OK sign. You’ll have to zoom in to see the crescent coming through the small aperture.

Google Maps routed me through Champaign, Illinois, on my way home, so I ordered a Papa Del’s pizza when I was about an hour away and took it home for a late dinner. I got home just as the Men’s National Championship game was starting. I watched it while eating pizza—the perfect end to a perfect day.
Moment diagrams for continuous beams
April 6, 2024 at 1:21 PM by Dr. Drang
As promised last time, we’ll now work out the solution for this three-span continuous beam with a uniform distributed load.
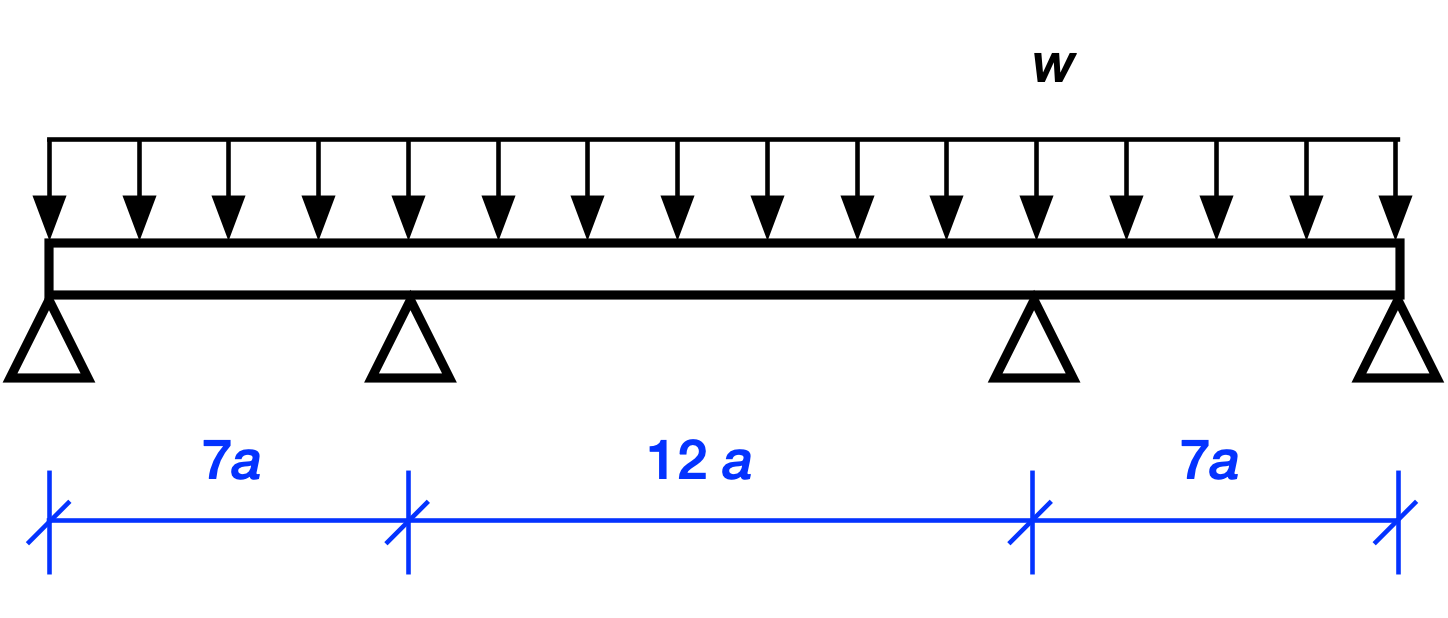
Because there are four unknown reaction forces at the supports and only two equations of statics1, we can’t solve for the reactions by statics along. This means the structure is statically indeterminate. And because there are two more unknowns than equations, we say that it has two degrees of indeterminacy.
But wait, can’t we use symmetry in addition to statics to solve for the reactions? After all, symmetry tells us that the two interior support reactions must be equal and the two exterior support reactions must also be equal.
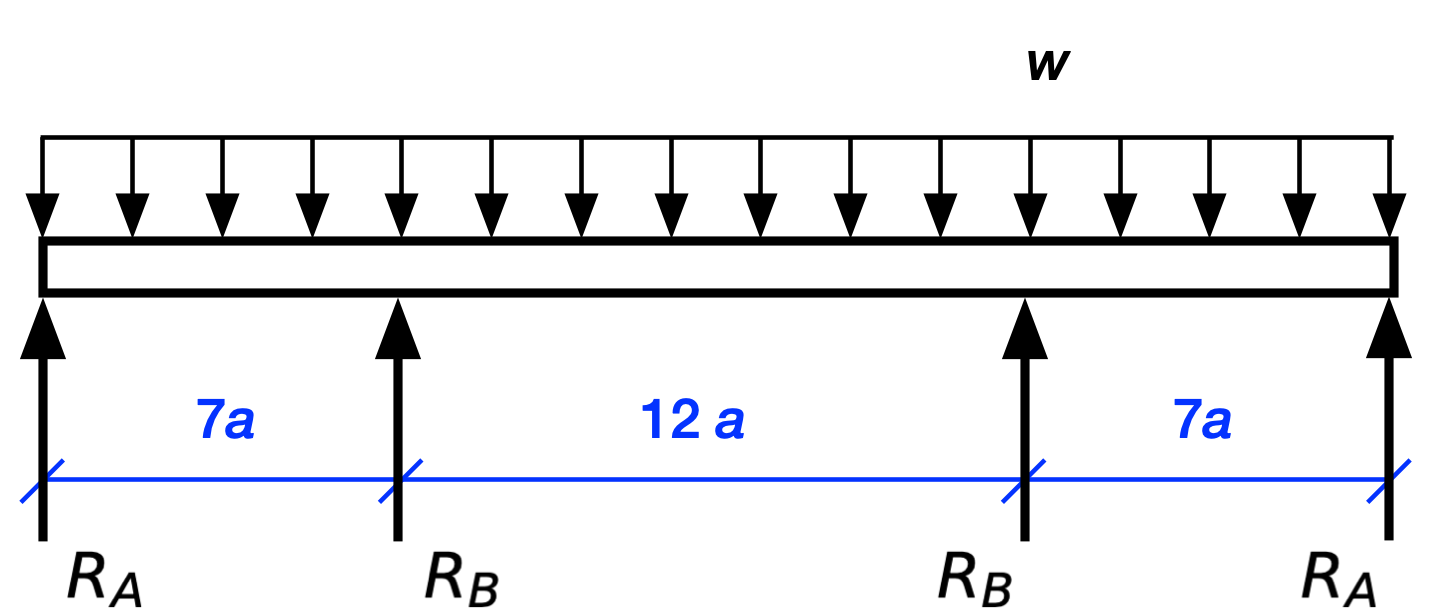
Let’s see what we can do with this. The equations of equilibrium for vertical loading and the moment about the left support are
These may look like two equations, but they really aren’t. After some algebra, they become
which are the same equation. So our two equations of statics aren’t independent and we really have one equation with two unknowns. That’s only one degree of indeterminacy, which is an improvement, but still isn’t enough to solve the problem through statics alone. And if you think you can get an independent equation by taking moments about another point, go ahead and try. I’ll be here when you come back.
To solve this problem—and to solve indeterminate problems in general—we have to account for the stiffness of the structure. There are many ways of doing this. If it were 1980 and I were still an undergraduate, I’d probably use moment distribution, because that was the standard way to do problems by hand back then. I suspect that most engineers today would use the finite element method. That’s the most practical solution, but letting your computer do all the work is no fun.
The fun way is to take advantage of symmetry and use Castigliano’s Second Theorem. Alberto Castigliano was a 19th Century Italian engineer whose 1873 thesis, Intorno ai sistemi elastici or Regarding elastic systems2 included his theorems and their proofs. You probably haven’t heard of Castigliano—he’s no Newton or Euler or Bernoulli—but there aren’t many dissertations whose findings are still being taught a century and a half later.
Castigliano’s Second Theorem is based on work and energy principles. Say we have a linearly elastic structure—that’s one where the deflection is a linear function of the loading and the structure springs back when the loads are removed. If we have a set of concentrated external loads acting on the structure, , we can express the strain energy, , as a function of those loads. Then the deflections, , of the points of load application in the directions of the , can be determining from the partial derivatives of the strain energy with respect to the loads:
The strain energy in a beam can be written in several ways. When solving problems by Castigliano’s Second Theorem, we write it in terms of the bending moment like this:
That’s the theory. Now let’s talk about the practice.
The strategy when using Castigliano’s Second Theorem to solve a statically indeterminate problem is the following:
- Remove the “extra” supports, i.e., the ones that are making the structure indeterminate. Since any of the supports could be considered extra, you have some freedom here. With experience, you’ll choose supports that make your calculations easy.
- Replace the supports with the forces (as yet unknown) that act at those supports
- Write out an expression for the strain energy in terms of the replacement forces.
- Take the partial derivatives of the strain energy with respect to those forces.
Set the partial derivatives to zero because the displacements at the supports that were removed are zero, i.e.,
- Solve the equations in Step 5 for the replacement forces.
The procedure is easier to show than it is to tell. Here’s our structure with the interior supports replaced by forces.
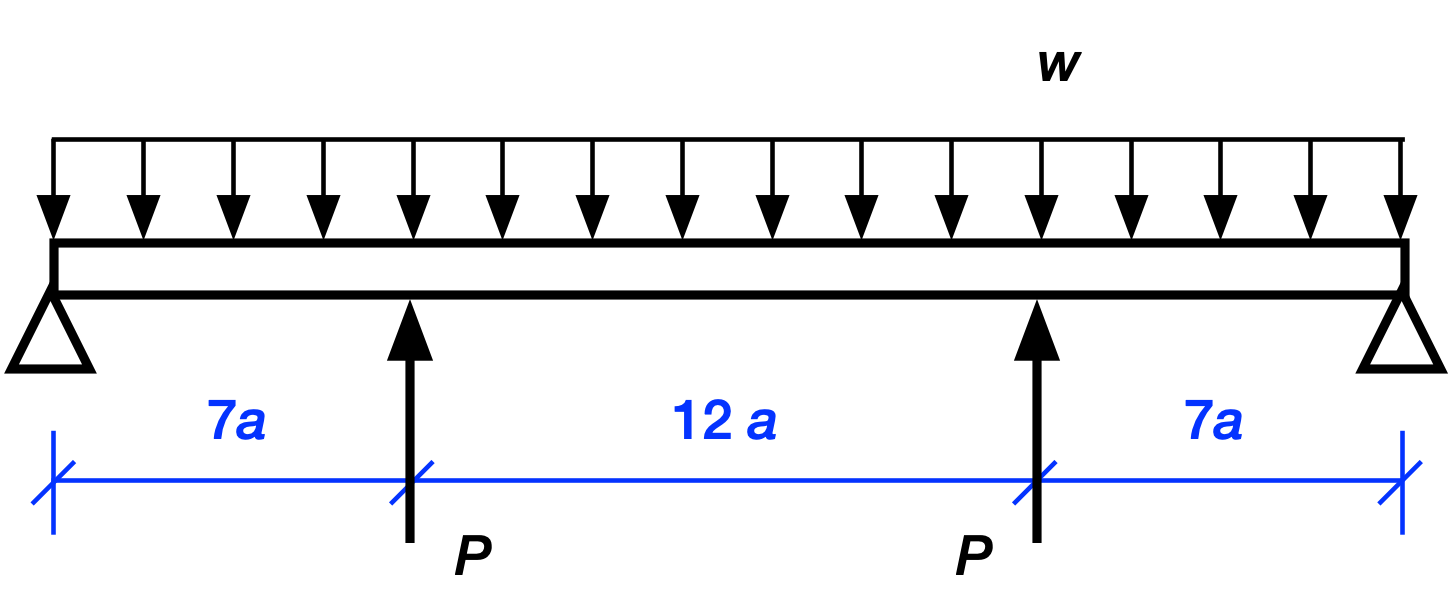
The two interior concentrated loads are equal because of symmetry. Since this is a linearly elastic structure, we can use superposition to analyze this complex loading. That is, we can break the complex loading into two or more simpler loading conditions that are easy to solve. After solving for the simpler loads, we add them together to get the solution for the complex loading. In graphical language, we do this:
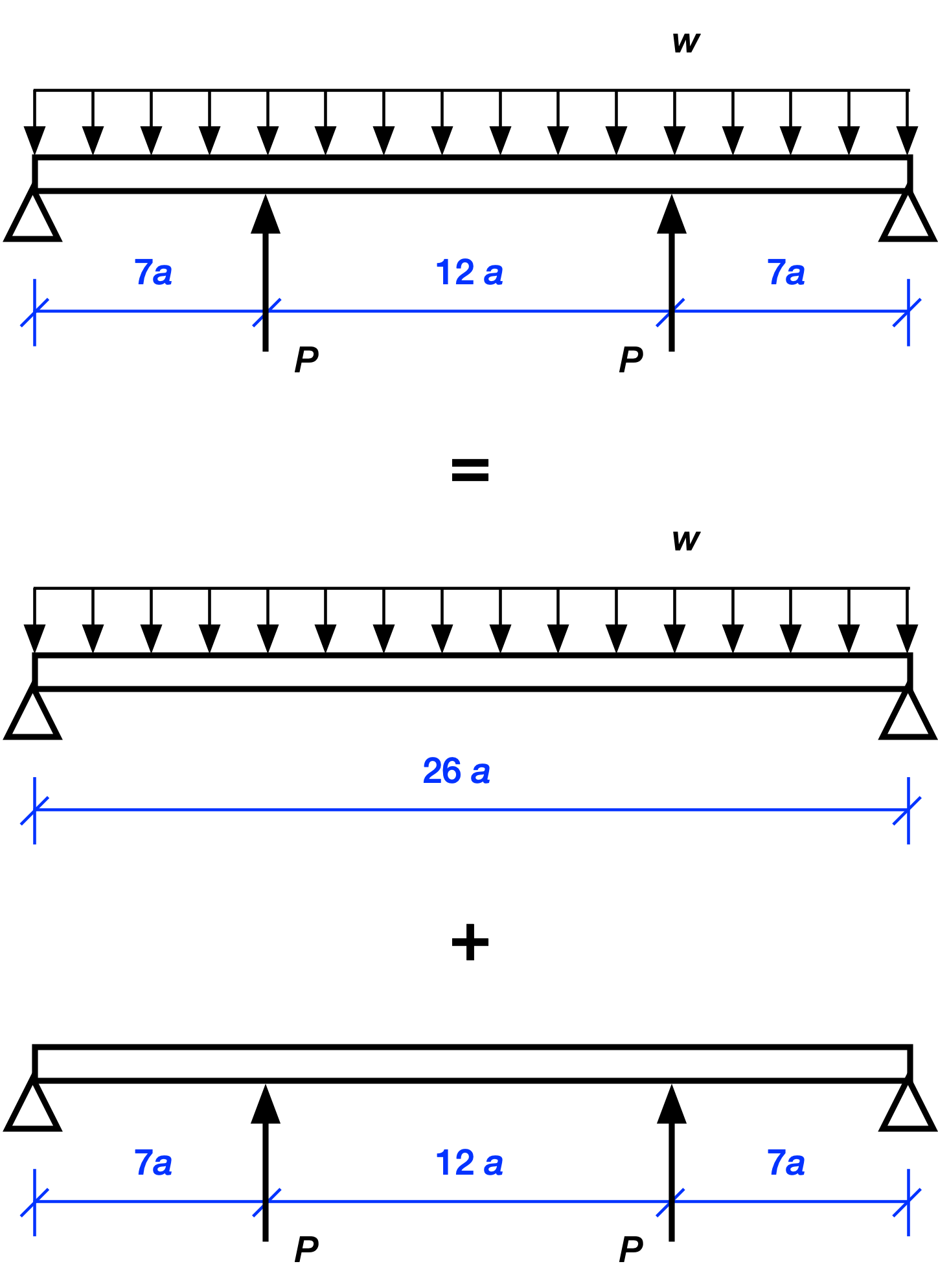
Let’s start with the reactions at the ends. Clearly, the upward reaction forces at the end supports are
where the first term is what the reaction would be if only the uniformly distributed load were acting and the second term is what the reaction would be if only the two interior point loads were acting. The sign of the term is negative because the reactions from the s alone would be downward.
The moment diagrams for two simpler load conditions are this for the uniformly distributed load
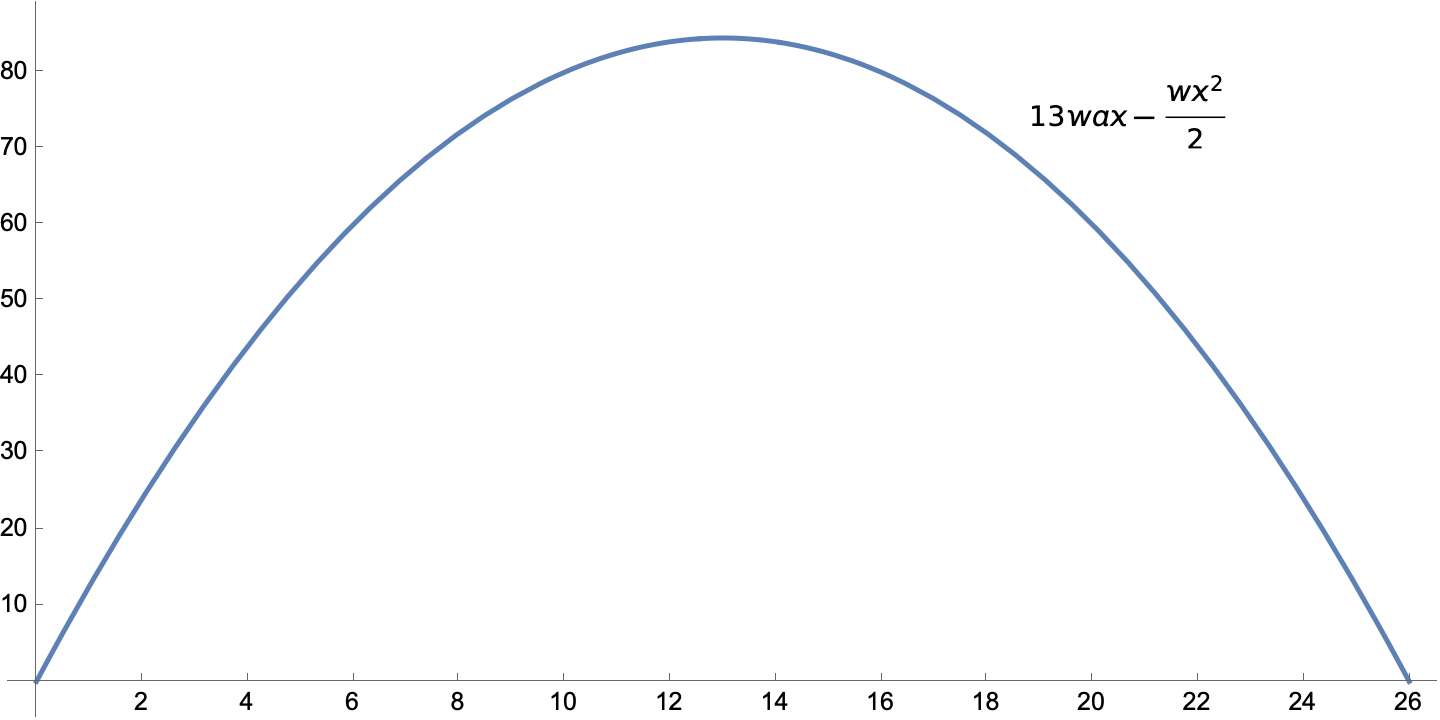
and this for the two concentrated loads.
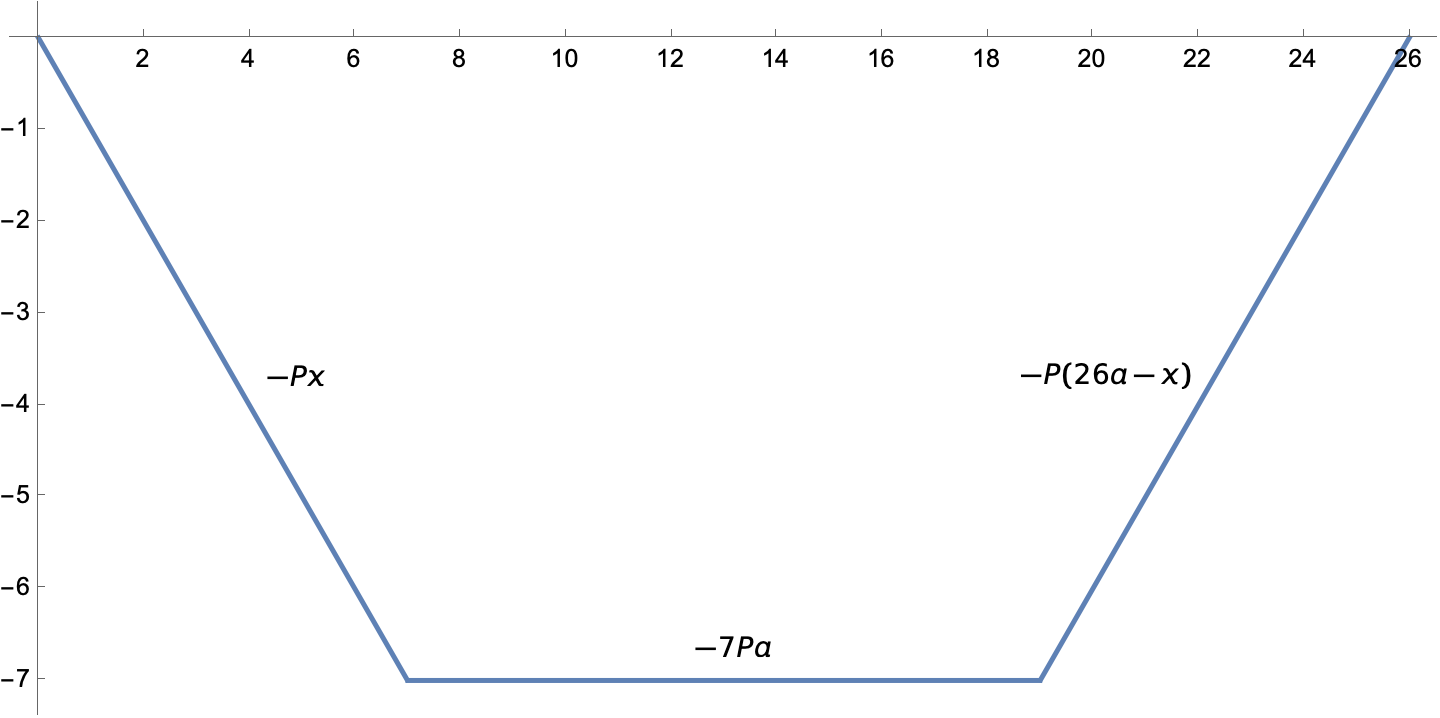
Concentrated loads put kinks in the moment diagram.
When we add the two moments together, we get this piecewise expression:
For each piece, the first two terms are due to the distributed load and the last term is due to the concentrated loads.
With the bending moment defined in terms of the unknown, , we can use the equation above to get the strain energy. I’m not going to pretend I did it by hand; here’s the Mathematica code,
M1 = 13*w*a*x - w*x^2/2 - P*x;
M2 = 13*w*a*x - w*x^2/2 - 7*a*P;
M3 = 13*w*a*x - w*x^2/2 - (26 a - x)*P;
U = Integrate[M1^2/(2*EI), {x, 0, 7*a}] +
Integrate[M2^2/(2*EI), {x, 7*a, 19*a}] +
Integrate[M3^2/(2*EI), {x, 19*a, 26*a}]
which gives us a strain energy of
When you give Mathematica integer input, it gives you integer or rational output, hence the large numbers in the numerators.
Taking the partial derivative of this with respect to and setting it to zero,
soln = Solve[D[U, P] == 0, P]
gives us
We plug this back into the expression for and get
To plot the moment diagram in Mathematica, we do what we did last time: divide the moment expressions by and introduce a nondimensional length variable, . The code is
m1 = M1/(w*a^2) /. {soln[[1]][[1]], x -> u*a};
m1 = Simplify[m1];
m2 = M2/(w*a^2) /. {soln[[1]][[1]], x -> u*a};
m2 = Simplify[m2];
m3 = M3/(w*a^2) /. {soln[[1]][[1]], x -> u*a};
m3 = Simplify[m3];
Plot[Piecewise[{{m1, u <= 7}, {m2, 7 < u <= 19}, {m3, u > 19}}], {u, 0, 26},
ImageSize -> Large, PlotStyle -> Thick,
Ticks -> {Table[t, {t, 0, 26, 2}], Table[t, {t, -12, 10, 2}]}]
where again the Piecewise function lets us split the function being plotted into pieces. Note also that we’re using the soln expression that came from the solution for to plug that into the various expressions.
The resulting plot is
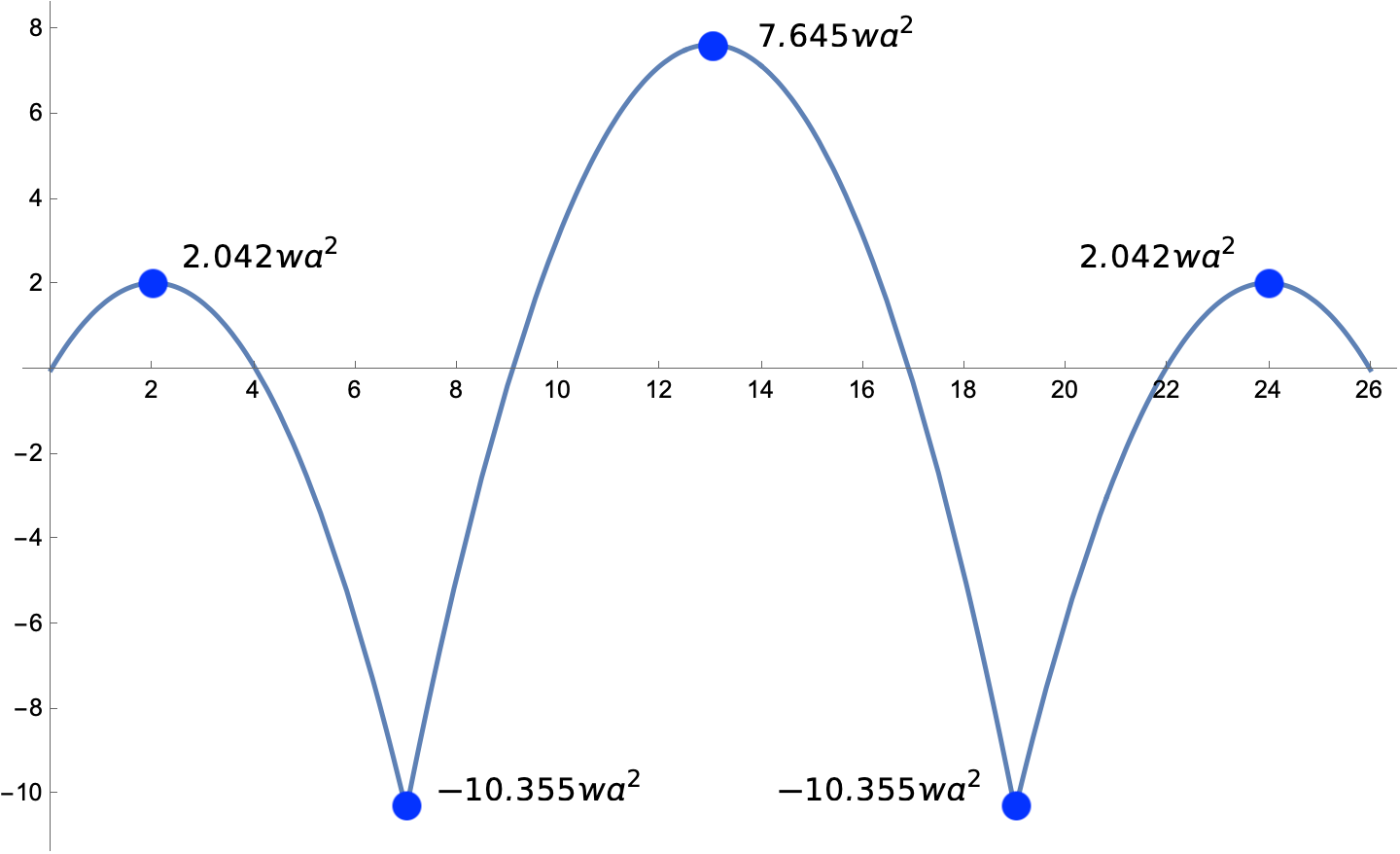
except that I added the annotations in Preview.
I’ll spare you the work involved in making the third moment diagram in the Francis Scott Key Bridge post, the one for a beam with the left interior support missing. The process is the same as what we just went through.
I should mention, though, that although this seems complicated when every step is explained, most structural engineers would be able to whip through this analysis quickly. They wouldn’t have wasted time showing that symmetry doesn’t make this problem statically determinate. They would know immediately to use superposition. And they’d draw the two moment diagrams for the simpler problems as fast as their pencil could move. That’s how expertise works.
-
Recall that the horizontal equilibrium equation gives us no information because there are no horizontal forces. ↩
-
Google Translate told me the English translation was Around elastic systems, which seemed off. I thought Google was taking “itorno” too literally; it should be something like “on” or “about.” So I asked Federico Viticci what he thought, and he gave me “regarding” as a good translation of an older Italian usage. Thanks, Federico! ↩

