Obscuring my location more than necessary
July 24, 2024 at 3:06 PM by Dr. Drang
In yesterday’s post, I obscured my location by covering up the latitude and longitude after the decimal point.
How good is this? How big is the area that could be covered by these truncated coordinates?
Well, you could cheat by using, say, ArcGIS to create a map of the Chicago area bounded by lines of latitude (parallels) at 41°N and 42°N and lines of longitude (meridians) at 88°W and 89°W. Like this:
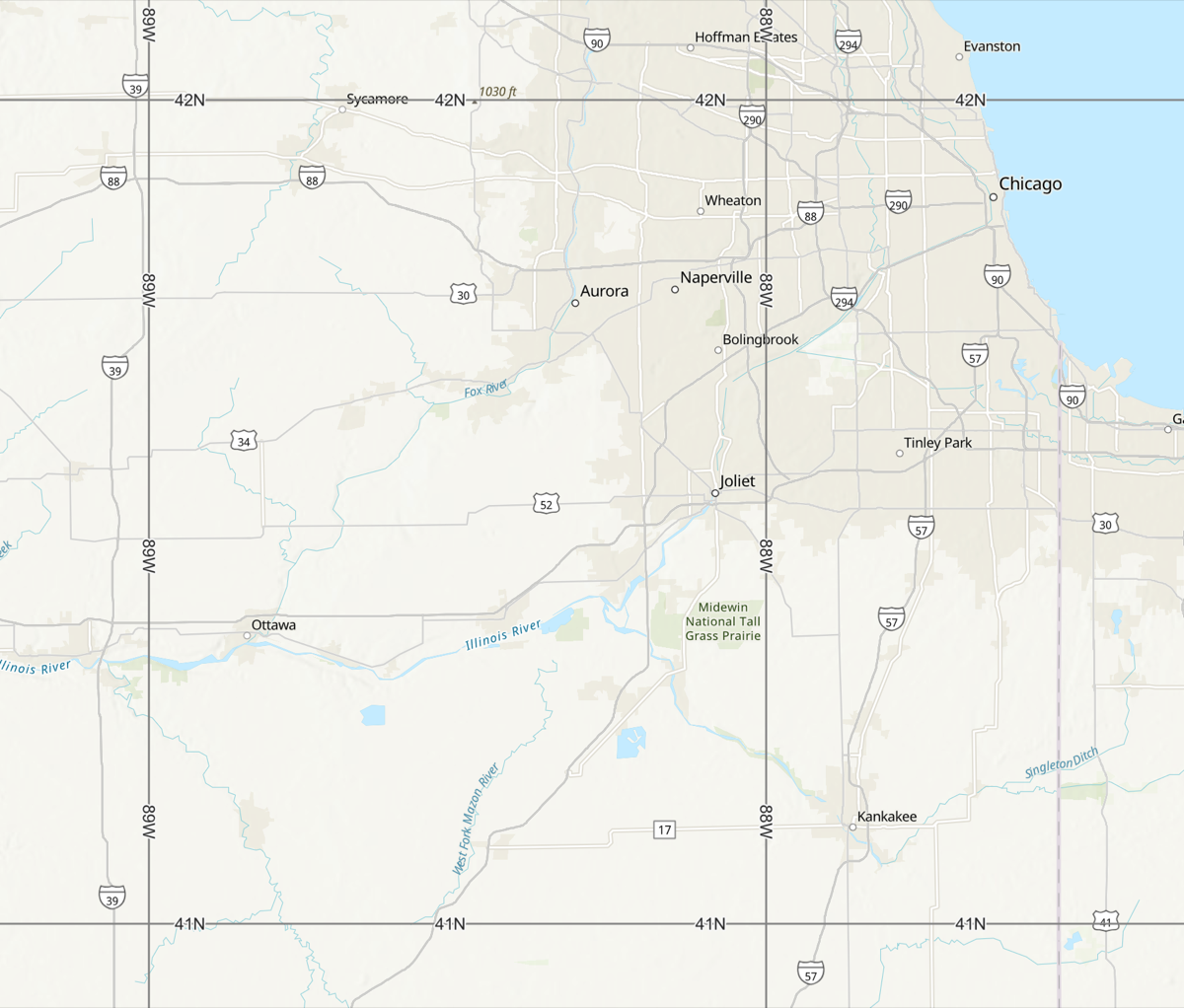
That’s obviously a pretty big area, and ArcGIS has measuring tools so you can get the lengths of the parallels and meridians. But you don’t need all this fancy stuff; you can get an estimate much more quickly with some simple calculations in your head or on a calculator.
The primary thing to know is that a nautical mile was originally defined as the distance on the Earth’s surface along one minute of arc. One degree is sixty minutes, so a very quick (and rough) estimate of the area would be a square that’s 60 miles on each side.
For some purposes—like my desire to obscure my location—this estimate is good enough. I’ve never made a secret of the fact that I live in Naperville, so I’ve already given up a more precise indication of my location than a 60-mile by 60-mile square, even if those two 60s are way off.
But if you need a significantly better estimate, you can calculate one with just a little more effort. The two biggest sources of error in the calculation above are:
- Nautical miles aren’t statute miles, they’re about 15% longer.
- Meridians converge as you get further from the equator. The convergence goes with the cosine of the latitude.
So our 1° long meridian is about 69 miles long. That takes care of the north-south distance. To get a better estimate of the east-west distance, we can multiply that 69 miles by the cosine of the average latitude,
to get 51.7 miles. This is why a 1° by 1° “square” looks more like a rectangle on a map.
I first thought I’d leave the first decimal place visible in the latitude and longitude figures. That would give me a rectangle of uncertainty of about 5 by 7 miles—good enough for my purpose. But as I was drawing the little checkerboard areas on the Tot screenshot, I found it much easier to use the decimal points as the left edges.
Tot Notes
July 23, 2024 at 5:50 PM by Dr. Drang
Against my better judgment, I decided to write a Shortcut today. Even worse, I wanted it to be able to run on my Apple Watch. After several iterations, all of which looked to me to be functionally identical, I finally hit upon one that worked.
The goal was to have a complication on my watch that I could tap, dictate a short note to, and have the note saved to Tot with time and location stamps. Like this (but without the checkerboards to obscure my location):

The complication that runs the Shortcut is at the bottom center of the Modular face, which is the one I normally use. This makes it handy for whatever ideas or observations I want to record when I’m out hiking or kayaking.

I can, of course, run it from my phone, too, but the main point of writing this Shortcut was to have a quick way of making notes like this when the phone isn’t handy.
You can download the Tot Notes Shortcut from its iCloud link. Here’s an annotated view of all the steps:
| Step | Action | Comment |
|---|---|---|
| 1 |  |
Ask the user to dictate some text. This will be the note. |
| 2 |  |
Get today’s date and time. |
| 3 |  |
Format the date and time as yyyy-mm-dd HH:MM:SS. |
| 4 |  |
Get the current location. |
| 5 |  |
Get the latitude of the current location. |
| 6 | 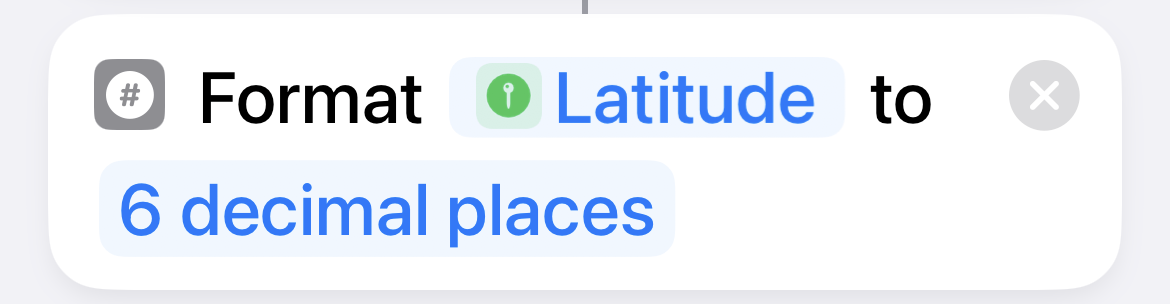 |
Truncate the latitude to 6 decimal places. |
| 7 | 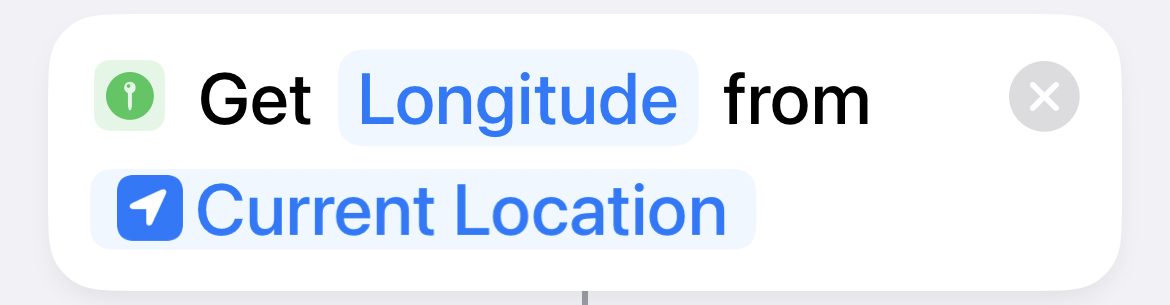 |
Get the longitude of the current location. |
| 8 | 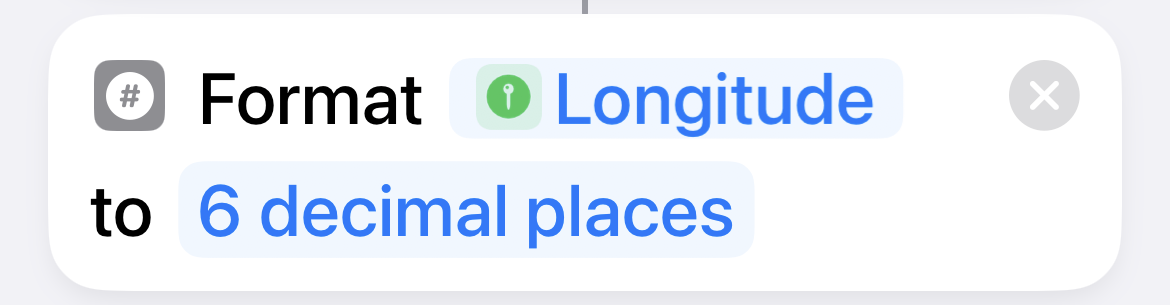 |
Truncate the longitude to 6 decimal places. |
| 9 | 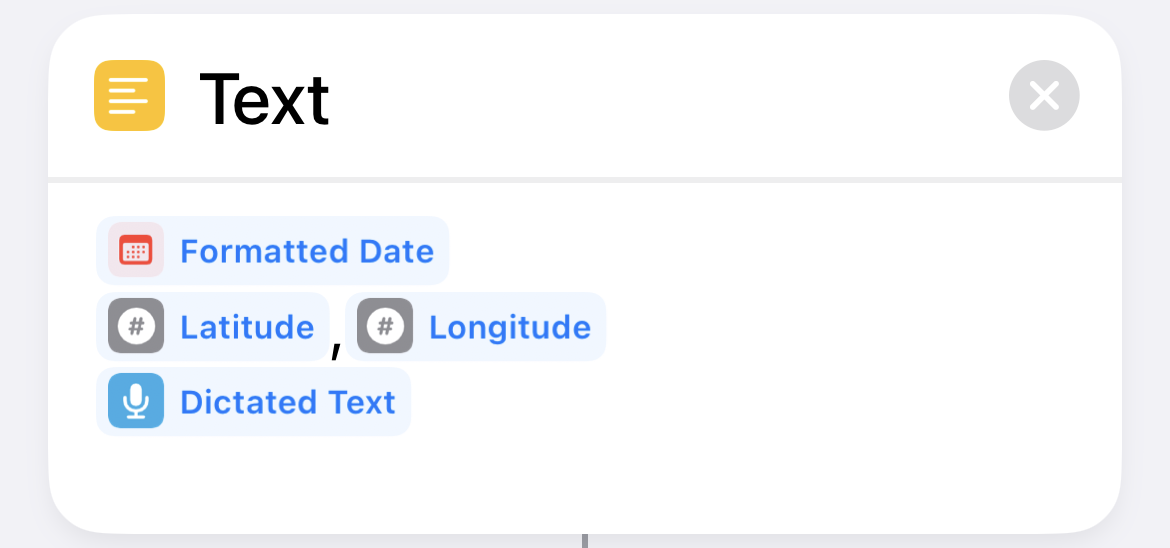 |
Put the date, time, latitude, longitude, and note into a paragraph with a trailing newline. |
| 10 | 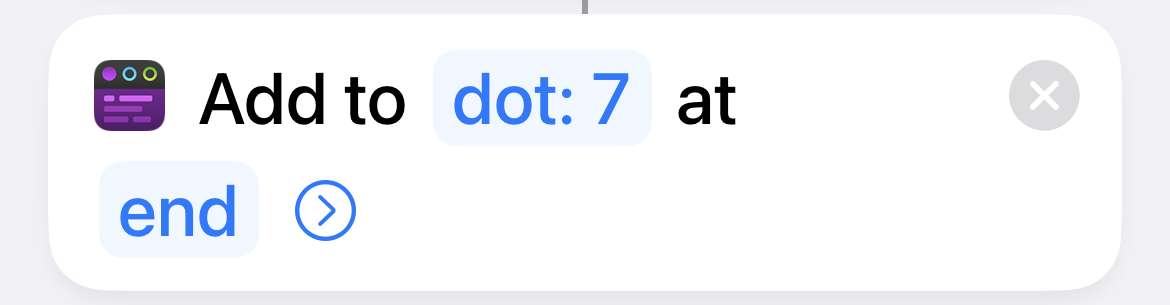 |
Add the paragraph to the end of Tot dot #7. |
As I said at the top, this is what I came to after quite a lot of backing-and-forthing with code that should have worked exactly like this version. Every earlier version did work when run from my phone; it was only this version that finally worked when run from the watch. That’s Shortcuts for you.
You may be wondering why I’m using Tot instead of Drafts. First, I bought Tot when it was on sale a few weeks ago, so it’s at the top of my mind right now. Second, while it’s nice that Drafts isn’t limited to just seven documents, I was worried that my notes would get lost in its infinitude. Tot’s limitations impose (I hope) a discipline that will have me going through my dictated notes and clearing them out frequently.
Followup on Wolfram county data
July 16, 2024 at 12:34 PM by Dr. Drang
You may remember a post I wrote back in December about inexplicable holes in US county-level data in the Wolfram Knowledgebase. I say “you may remember” because I certainly didn’t until I got an email from Wolfram last week telling me that the holes had been filled. Yes and no, as it turns out.
I first discovered the problem in August of last year. I wanted to use Mathematica to get a list of all the county seats in Illinois, and I noticed that the data for DeKalb and DuPage counties were missing. It wasn’t available through a Mathematica function call or through a WolframAlpha query. Given that Wolfram is based in Illinois, I thought this was a particularly glaring error, so I sent them feedback.
By the time I wrote the post in December, I had looked into the issue further and discovered that the Knowledgebase was missing county seats for counties all over the country. I didn’t follow up with Wolfram on that because I thought they’d already memory-holed my original complaint.
But no! The email that came last week told me that the problem (for Illinois) had been fixed and said I could go to this link to see for myself. If you follow the link, you’ll have to tap the More button on that page, but when you do, you’ll see that DeKalb and DuPage counties now have their county seats. Which is nice.
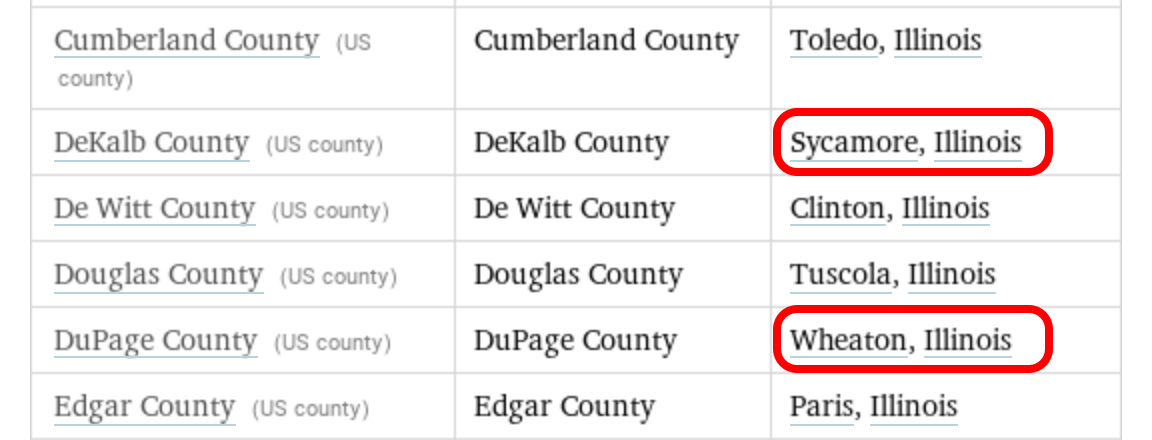
I changed the WolframAlpha query to look for California counties and found that the county seats for Mono and Sierra counties had also been filled in. Similarly for DeKalb and LaPorte counties in Indiana. So it looked like Wolfram had cleaned up the data across the country.
But that was in WolframAlpha. When I tried to get the same information through an equivalent function call in Mathematica, the county seats for DeKalb and DuPage were still missing.
It might not be immediately obvious, but if you look carefully, you’ll see Missing[NotAvailable] in the 19th and 22nd positions of the list.
The same problem can be found in other states: county seats that now appear in WolframAlpha on the web are still missing from the equivalent Mathematica function calls. This inconsistency is even weirder than the original missing data. How can calls to what should be the same database produce different results?
So I’ve sent feedback on this to Wolfram, and I’ll let you know when they answer. Given their previous speed, you can expect that post sometime next June.
A good (or bad) example
July 9, 2024 at 3:24 PM by Dr. Drang
The one rule of plotting that every newly minted data scientist can repeat without fail is that your graphs should always start at zero. A graph that doesn’t start at zero is misleading, dishonest, and possibly nefarious. This rule is, of course, bullshit. Not a rule at all.
Oh sure, there are plenty of times when you should start at zero, but the best range to plot depends on what you’re plotting. This morning I saw a great example of a plot that started at zero when it really shouldn’t have.
It’s in an app that, among other things, is tracking my weight. Here’s the graph:
Because my weight over these seven days hasn’t changed by more than about 1.5%, the columns are all basically the same height. Even if I were to lose a lot of weight, I’d never go anywhere near zero. The only useful part of this chart is labeling over the columns—it could just as well be a table.
Where should the y-axis start? Depends on what the graph is being used for. If I had a target weight, I’d probably start at some round number below that target. I might put a thin horizontal line at the target. But I’d never do this.
The makers of the app have either internalized the rule that isn’t a rule or have decided that following it fends off criticism by idiots who think it is a rule. Too bad.

