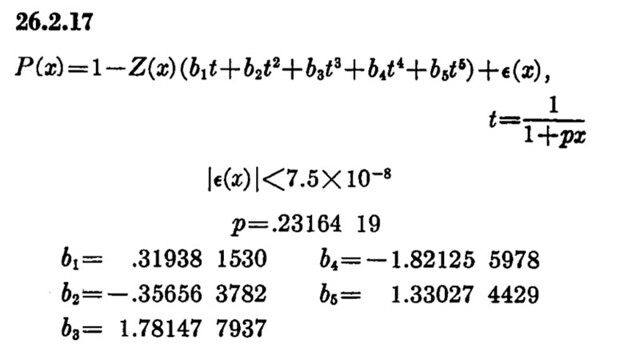And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

PCalc 2.8

May 1, 2013 at 11:11 AM by Dr. Drang

If you followed my advice back in December, you bought PCalc for the ridiculously low price of 99¢ during its 20th anniversary sale¹ and have been using a first-class calculator for the past four months. With Version 2.8 just released, you’re going to see its value explode with two new features: user-defined conversions and user-defined functions.

PCalc added an f(x) key in Version 2.6 as a way to access functions beyond those available on the keys. Initially, the additional functions were limited to whatever the developer, James Thomson, gave us. Here’s me, back in December:

What I’d really like to see, though, is an expansion of these functions. Things like present value, future value, and internal rate of return are natural for the financial section. And the statistical section could use functions for the normal and inverse normal cumulative distribution.

This was not based on any insider knowledge. High-end calculators have been programmable since the 70s, so it was only natural to expect that functionality to come to PCalc eventually. We just had to wait for James to figure out how he wanted to implement it.²

In this post, I’m going to focus on creating user-defined functions. The creation of user-defined conversions follows almost exactly the same steps and has access to the same set of commands—once you’ve learned how to define functions, you’ll have no trouble defining conversions.

Creating a new function

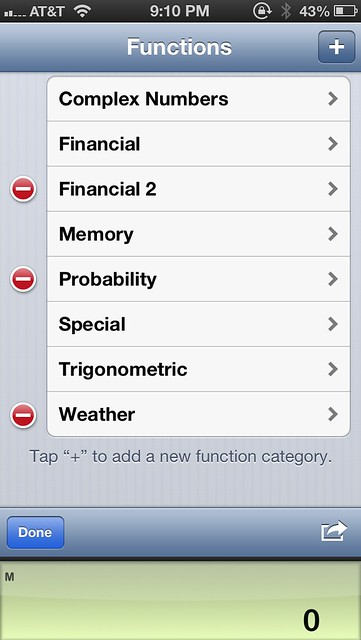
Start by tapping the f(x) key to see the list of function categories and then tap the Edit key in the lower left corner. You’ll get a ⊞ key in the upper right corner, which will allow you to add new categories. As you can see below, I’ve added three categories: Financial 2, Probability, and Weather.

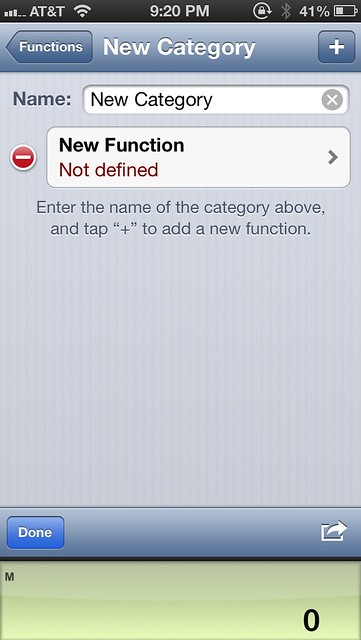
Tapping the ⊞ key on this screen will create a new category. Tapping that category takes you to a screen where you can rename it and then start defining new functions.

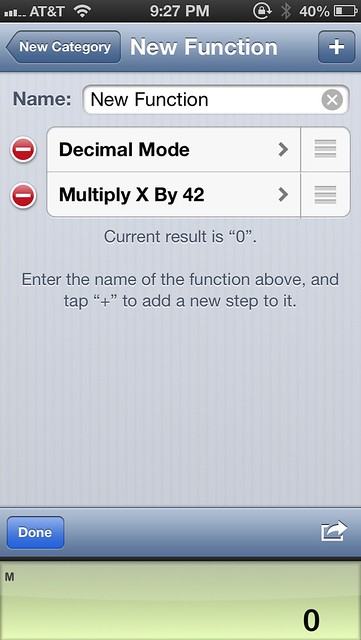
Tapping the new function takes you to a screen where you can rename and define it. PCalc starts you off with two commands: one that puts you in decimal mode (if you weren’t already there) and one that multiplies the current value by the universal constant.

You can change these by tapping them, which will take you to a command editing screen we’ll discuss in a bit, and add new commands by tapping the ⊞ key.

The command set

PCalc gives you 39 commands from which to build your function. Here they are, with descriptions, as they appear in the scrolling list you see as you construct your function.

Seven of the commands have only one part—the command itself with no arguments. These are typically commands that set the calculation mode, like the Decimal Mode command we saw above or the Radians Mode command.

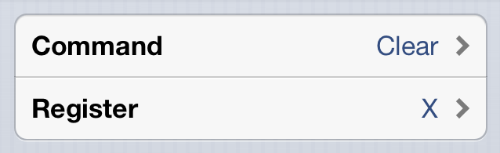
Seventeen of the commands have two parts, in which you have to choose both the command itself and a single argument. The trig, log, and exponential commands work this way, as does the Clear command.

We’ll discuss how to set the argument in a bit.

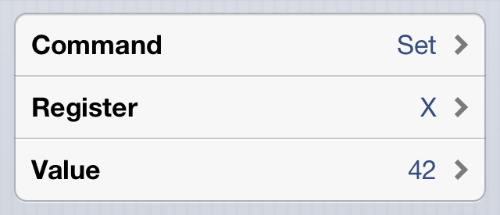
Nine of the commands have three parts: the command and two arguments. The basic arithmetic commands (My Dear Aunt Sally) fall into this category, as does the command that sets a register.

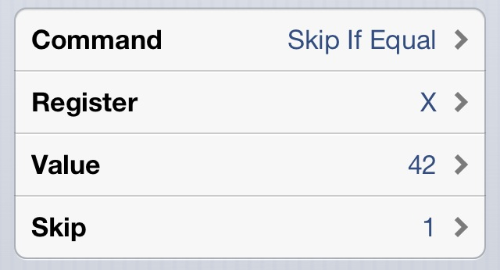
Finally, six of the commands have four parts: the command and three arguments. These are all branching commands that test one value against another and skip a given number of steps if the test is true.

Variables and constants

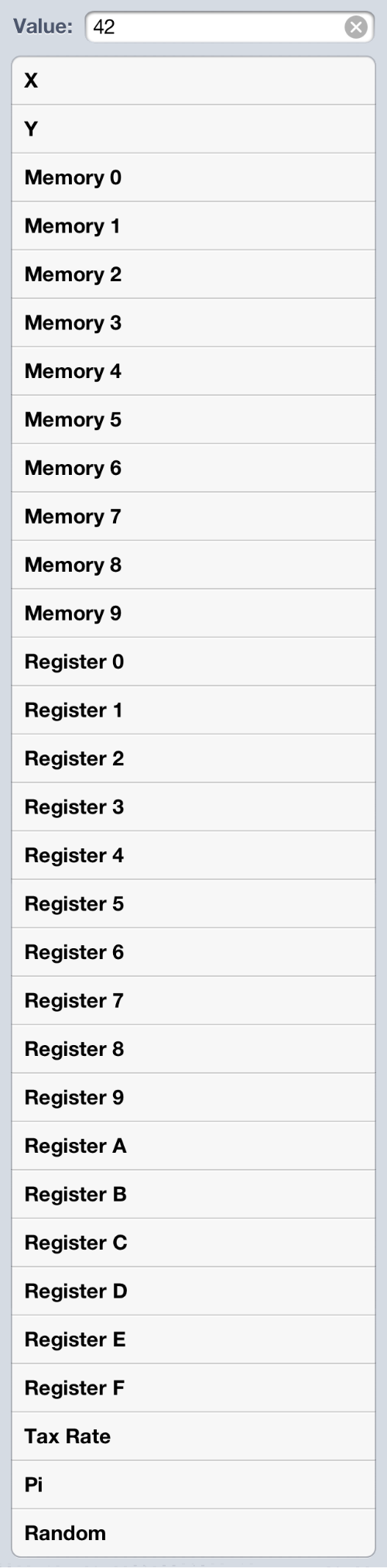
Numerical functions need places where they can store numbers and retrieve them from. PCalc provides 29 such places: the X and Y registers, ten memory locations, sixteen registers, and a special register called Tax Rate used in some of the builtin financial functions. In addition to these read/write variables, there are three read-only constants: Pi (π), a uniformly distributed random number between 0 and 1,³ and a user-defined constant called Value.

Here’s PCalc’s scrolling list of variables and constants you can choose from. If you’re setting or changing a value, the constants don’t appear in the list.

The X and Y registers and the memory locations are accessible any time you’re using PCalc. Registers 0-9, A-F, and the Tax Rate are accessible only through the programming environment; they’re the best place to store intermediate results because they don’t alter what the user has stored in memory.

At present, PCalc does not clear these registers after a function is calculated. The Tax Rate register will certainly stay this way, but I don’t know if that’s true about the others, so you’re taking a bit of a risk if you write functions that rely on their persistence.

Update: James says the persistence of the registers is part of the design, so it’s safe to take advantage of that if you want.

A simple example

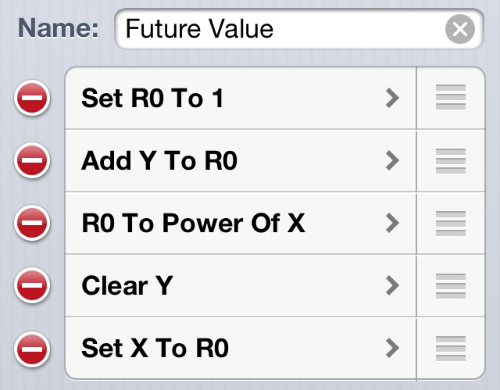
Let’s look at a five-step function for calculating the future value of an investment. The formula is elementary:

$$FV=PV(1+i{)}^n$$

where $FV$ is the future value, $PV$ is the present value, $i$ is the interest rate per compounding period, and $n$ is the number of compounding periods.

The function I defined calculates just the $(1+i{)}^n$ part. It gives, in effect, the multiplier associated with the compounding. Here’s the function defined in PCalc:

It expects the interest rate in the Y register and the number of compounding periods in the X register; it returns the future value multiplier in the X register. To run this function in RPN mode, which is what I use, you type in the interest rate, tap Enter, type in the number of compounding periods, and then select the Future Value function from under the f(x) key. In algebraic mode, you type in the interest rate, tap the x~y key, type the number of compounding periods, and then select the Future Value function from under the f(x) key. It’s the same amount of work either way.

James has decided that functions that need more than two arguments will have to use the memory locations for the extra arguments. I’d much prefer to be able to load up the RPN stack with all my arguments (it’s faster than entering values into memory), but that would leave the algebraic users out in the cold.

Sharing functions

You can share the functions you write with others by tapping the share button and sending an email with the functions bundled up in an attachment. When the recipient gets the email, she can tap on the attachment and choose to import them into her copy of PCalc.

It’s my understanding that functions you define on one iOS device will be automatically available on your other iOS devices through iCloud syncing. With only an iPhone, I have no way of testing this.

Programming on your computer

For functions with only a few steps, the tap-scroll-tap method of creating functions on an iPhone or iPad is just fine. But for more complicated functions, it’s easy to get lost and make mistakes. Fortunately, there’s a way to program PCalc in your favorite text editor.

When you send an email with a shared bundle of functions, the attachment is a plist file with a .pcalcfunctions extension. If you save this file to your computer, you can open it in a text editor to see the usual plist structure. Each function is a <dict>, with its code stored in a string using a compact little language. Here’s definition of the Future Value function described above:

xml:
<key>function.user.579085775.3922504026</key>
<dict>
  <key>Code</key>
  <string>set r0 1; add r0 y; pwr r0 x; clr y; set x r0</string>
  <key>Name</key>
  <string>Future Value</string>
</dict>

If we rearrange the string of code, it’s easy to see how it relates to our definition above.

set r0 1
add r0 y
pwr r0 x
clr y
set x r0

This shows us the path to writing long, complicated functions:

1. Create a new function in PCalc. Give it the name you want and put it in the category you want, but don’t bother changing the definition from the two-command default we saw near the top of the post.
2. Share that function with yourself via email. Open the email on your computer and save the attached .pcalcfunctions file to disk.
3. Write the function you really want in the little language used in the ,pcalcfunctions plist. I write mine with each command on its own line and then do a search-and-replace to turn it into a long, semicolon separated string.
4. Replace the default commands in the .pcalcfunctions file with what you just wrote.
5. Send yourself an email with the edited .pcalcfunctions file attached.
6. Open that attachment on your iOS device to install the redefined function. It’ll replace the old definition.

This may seem like too many steps, but it’s much easier than writing a long function directly in PCalc.

One of the functions I wanted is the cumulative distribution function for the standard normal. There is one of those integrals that can’t be performed analytically, so it has to be approximated. Here’s a good approximation from Abramowitz and Stegun:

And here’s that formula (generalized to handle negative arguments) converted into a PCalc function:

set r0 x
bgt x 0 1
  neg r0
set r1 r0
mul r1 .2316419
add r1 1
inv r1
set r2 r1
mul r2 .319381530
set r3 r1
pwr r3 2
mul r3 -.356563782
add r2 r3
set r3 r1
pwr r3 3
mul r3 1.781477937
add r2 r3
set r3 r1
pwr r3 4
mul r3 -1.821255978
add r2 r3
set r3 r1
pwr r3 5
mul r3 1.330274429
add r2 r3
pwr r0 2
div r0 2
neg r0
exp r0
set r3 2
mul r3 pi
pwr r3 .5
div r0 r3
mul r0 r2
blt x 0 3
  set x 1
  sub x r0
  stp
set x r0

It’s much faster to type the lines than to scroll through the list choosing commands and registers, and it’s easier to see the overall logic this way.

All the command abbreviations

The main difficulty in writing PCalc functions in a text editor is figuring out what the abbreviations are for each of the commands. To help with this, I created, in PCalc, a fake function with 37 steps—one for each of the commands. After sharing this function and opening the .pcalcfunctions file on my computer, I extracted all the commands. Here they are with their default arguments and an explanatory comment:

set x 42      # Set X to 42
clr x         # Clear X
add x 42      # Add 42 to X
sub x 42      # Subtract 42 from X
mul x 42      # Multiply X by 42
div x 42      # Divide X by 42
neg x         # Negate X
inv x         # Invert X
pwr x 42      # Raise X to the power of 42
roo x 42      # Raise X to the power of 1/42
sin x         # Sine of X
cos x         # Cosine of X
tan x         # Tangent of X
asn x         # Arcsine of X
acs x         # Arccosine of X
atn x         # Arctangent of X
ln x          # Natural log of X
log x         # Base 10 log of X
exp x         # e to the power of X
e10 x         # 10 to the power of X
fac x         # Factorial of X
rnd x         # Round X to nearest integer
trn x         # Truncate X to nearest integer
hyp x 42      # Hypotenuse of triangle with legs X and 42
leg x 42      # Leg of triangle with hypotenuse and other leg of X and 42 
dec           # Decimal mode
hex           # Hex mode
oct           # Octal mode
bin           # Binary mode
deg           # Degrees mode
rad           # Radians mode
jmp 1         # Skip 1 step
beq x 42 1    # Skip 1 step if X is equal to 42
bne x 42 1    # Skip 1 step if X is not equal to 42
bgt x 42 1    # Skip 1 step if X is greater than 42
bge x 42 1    # Skip 1 step if X is greater than or equal to 42
blt x 42 1    # Skip 1 step if X is less than 42
ble x 42 1    # Skip 1 step if X is less than or equal to 42
stp           # Stop

These are in the same order as the screenshot list. Most of the names are immediately obvious; others take a little thinking to understand. The inverse power command, roo, is short for root.⁴ The b at the front of beq and the other skip commands is short for branch. The only one I’ve had trouble remembering is pwr, which I tend to type as pow.

Finally

A calculator isn’t necessarily the best tool for complicated analyses, but sometimes it’s the best tool that’s readily available. Because PCalc is in my phone, its capabilities—whatever they are—are always with me. The addition of user-defined functions allows me to do calculations away from my desk that I couldn’t do before.

This post wasn’t intended to be a breezy read. Its main purpose is to act as a reference to help you (and me) get new functions written. I don’t know if James intends to host a repository of functions at pcalc.com, but I’ll be putting all my functions in this GitHub repository. At present, it has three sets of functions:

• Financial 2.pcalcfunctions. This has the future value function shown above, a present value function, and a loan payment function.
• Probability.pcalcfunctions. This has the standard normal PDF, CDF, and inverse CDF.
• Weather.pcalcfunctions. This has functions for calculating the wind chill factor and the heat index.

The README is pretty rudimentary at the moment, but it does explain the inputs and outputs of each function. I’ll be adding better explanations of the underlying calculations soon.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang