Next post Previous post

Screwed up

November 27, 2013 at 11:39 PM by Dr. Drang

I’m deeply disappointed in each and every one of you. Last night, in the post about jacking up a bed to remove the headboard, I said

The jack’s leverage, meant to lift a car, was so great I could lift the bed by turning the screw with my fingers.

and none of you took to Twitter to correct me. While the jack certainly provides a huge mechanical advantage, to describe it as leverage isn’t quite right. The simple machine that does the work is an inclined plane, not a lever. As punishment for not picking up on my error, you’ll now have to sit through an explanation of how the jack works.

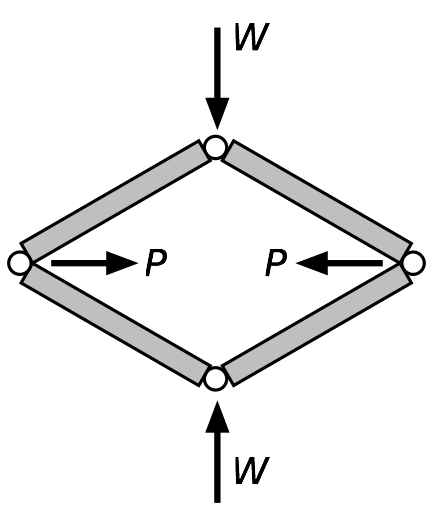
Here’s a picture of my car’s jack:

Jack

It’s basically a four-bar linkage (we can ignore the really short links at the top and bottom and treat them as single-pinned joints) with a threaded rod connecting the two side hinges. Here’s a schematic of the linkage with the forces acting on it,

Toggle full

where WW is the weight we’re lifting and PP is the force in the threaded rod. PP is what’s keeping the linkage from falling flat.

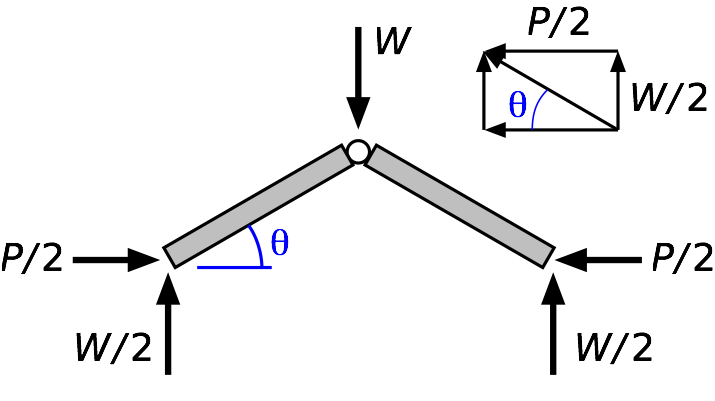
If we draw a free-body diagram of the upper half of the linkage

Toggle upper

and recognize that each bar is a two-force member (so the resultant force in each bar must act along the bar), we can use the little diagram in the upper right to relate PP to WW:

W/2P/2=tanθ\frac{W/2}{P/2} = \tan \theta

So

P=WcotθP = W \cot \theta

If you think about how the cotangent function works, you’ll recognize that this isn’t where we get the mechanical advantage needed to lift a car. In fact, for θ\theta less than 45°, PP is greater than WW, so there’s actually a mechanical disadvantage.

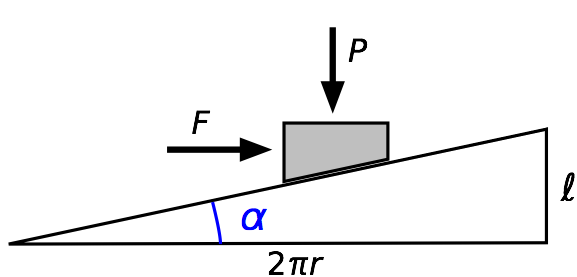
We need to turn our attention to the screw thread, which is how we generate the force PP. A screw thread is basically an inclined plane wound around a rod. If we unwind one turn of the thread, we can see that the angle of incline, α\alpha, is related to the pitch radius, rr, and lead, ℓ\ell, of the screw:1

tanα=ℓ2πr\tan \alpha = \frac{\ell}{2\pi r}

Unwound thread

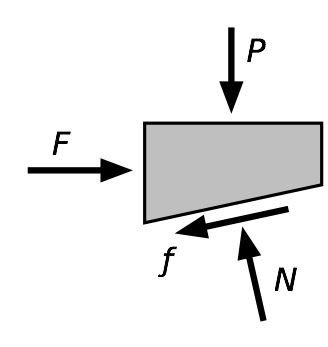
Turning a screw against a resistance, which is what we’re doing when using the jack to lift, is like pushing a block up the slope. The free-body diagram is

Sliding block

where NN is the normal2 contact force between the block and the plane and ff is the friction force between the block and the plane.

The equations of equilibrium in the horizontal and vertical directions tell us

F=fcosα+NsinαF = f \cos \alpha + N \sin \alpha

and

P=Ncosα−fsinαP = N \cos \alpha - f \sin \alpha

Since the block is sliding, f=μNf = \mu N, where μ\mu is the coefficient of friction between the block and the plane. Substituting this into the equilibrium equations and rearranging, we get

F=μ+tanα1−μtanαPF = \frac{\mu + \tan \alpha}{1 - \mu \tan \alpha} P

In a screw thread, where this inclined plane is wrapped around a rod, the force, FF, is acting at the pitch radius, rr, to produce a torque, TT. Therefore, the torque required to turn a screw against a resistance, PP, is

T=Fr=μ+tanα1−μtanαPrT = F\;r = \frac{\mu + \tan \alpha}{1 - \mu \tan \alpha} P\;r

My car’s jack has a single-threaded screw with 10 threads per inch, which means its lead, ℓ\ell, is 0.10″. Its pitch radius is 0.20″, so

tanα=0.102π(0.20)=0.0796\tan \alpha = \frac{0.10}{2\pi(0.20)} = 0.0796

Jack screw

The friction coefficient is always a tricky thing to estimate, but let’s assume it’s 0.20, which is reasonable for lubricated threads. Then the relationship between the torque applied to the screw and the force the screw applies to the linkage is

T=0.20+0.07961−(0.20)(0.0796)P(0.20in)=(0.0568in)PT = \frac{0.20 + 0.0796}{1 - (0.20)(0.0796)} P\;(0.20\; \mathrm{in}) = (0.0568\; \mathrm{in})\;P

Substituting in our earlier result for the linkage, we get this relationship between the torque and the lifted load:

T=(0.0568in)WcotθT = (0.0568\; \mathrm{in})\;W\; \cot \theta

For an angle of 30°, that means

T=(0.0984in)WT = (0.0984\; \mathrm{in})\; W

That small coefficient is where our mechanical advantage comes from.

Let’s say the bed I jacked up yesterday weighed 160 lbs. The jack lifted only about a quarter of that at any time, so the torque needed to lift it was 4 in-lbs. No wonder I could do it with my fingers.

Of course the jack is meant to lift a car, not a bed. The curb weight of my car is about 3200 lbs. To lift a quarter of its weight requires a torque of about 80 in-lbs. Even lifting half of its weight would be easy to do with the offset jack handle (which, unlike the jack itself, does use leverage).

The equation

T=μ+tanα1−μtanαWrcotθT = \frac{\mu + \tan \alpha}{1 - \mu \tan \alpha} W\;r \cot \theta

tells us that reducing friction will give us a greater mechanical advantage because it will decrease the numerator and increase the denominator. But if we reduce the friction too much, the jack won’t stay up on its own—the weight will cause the screw to turn backward and lower the load. We can derive the equation for determining the torque required to lower the load using the same ideas we used for lifting, but with FF and ff acting in opposite directions. It’s

T=μ−tanα1+μtanαWrcotθT = \frac{\mu - \tan \alpha}{1 + \mu \tan \alpha} W\;r \cot \theta

where this TT is acting in the opposite direction. Notice that if μ≤tanα\mu \le \tan \alpha, then T≤0T \le 0, which means the screw will unwind itself under load. For my jack, the friction coefficient needs to be greater than about 0.08 to prevent unwinding.

  1. The nomenclature of screw threads is more than I can explain here. Suffice it to say that if we consider a screw thread to be a series of peaks and valleys, the pitch radius is the average of the peak and valley radii. The lead is how far the screw advances in one turn. For more, see these two Wikipedia pages or a copy of the Machinery’s Handbook. ↩

  2. “Normal” here means “perpendicular,” not “average” or “everyday.” It’s the force at right angles to the plane of contact. ↩

Next post Previous post