And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

For fun it's a wonderful toy

March 8, 2014 at 7:01 PM by Dr. Drang

Yesterday, Allen MacKenzie pointed me to this Kottke post and made me think about what I’ve been doing here lately.

“Old school” reminded me that I used to write about more substantive things than my trouble with Mail. I’m not prepared to say anything yet about the chain fountain, but I have downloaded the paper and skimmed it, and it seems like something I could tackle. Instead, I’m going to write about a similar bit of magical mechanics that Kottke linked to quite a while ago: the levitating slinky.

People are fascinated by the fact that the bottom of the slinky doesn’t move until the top has come down to meet it. This clip was even featured on an episode of QI (where Stephen Fry makes the unpardonable error of saying “They can’t really explain quite why that happens.”). Personally, I think the slinky drop is less interesting than Newton’s cradle, but I suppose people have seen Newton’s cradle so often, they don’t find it surprising.

Kottke linked to this explanation by Rhett Allain at Wired, who makes a nice discrete model of the slinky and runs a simulation, but also gives this unsatisfying verbal explanation:

When it is let get, the center of mass certainly accelerates downward (like any falling object). However, at the same time, the slinky (spring) is compressing to its relaxed length. This means that top and bottom are accelerating towards the center of mass of the slinky at the same time the center of mass is accelerating downward.

This is certainly true, but it doesn’t explain why the bottom remains stationary until the slinky is fully compressed. “Both ends moving toward the center” could result in the bottom moving up or down.

The physicist in the videos on the Wired page gives the best explanation when he talks about a compression wave propagating down the slinky. He also invokes information theory as part of the explanation, which I find unnecessarily hifalutin’, but to each his own. I’ll stick to mechanics. And I’m going to stick the mechanics to you.

Let’s start by looking at a spring in its natural, unstretched state. This is not necessarily a slinky, just any old spring with length $L$, mass $m$, and spring constant $k$.

We set up an $x$ axis starting from the left end and call the displacement of any point on the spring $u$. Note that $u=u(x,t)$ is a function of both position $x$ and time $t$.

Now we’re going to examine a little chunk of the spring of length $\mathrm{\Delta }x$ and see what happens when a tension is applied to the spring.

The little bit stretches to new length of

$$\mathrm{\Delta }x+\frac{\partial u}{\partial x}\mathrm{\Delta }x$$

so its change in length is

$$\frac{\partial u}{\partial x}\mathrm{\Delta }x$$

According to Hooke’s Law, the change in length is related to the tension in that bit of spring by

$$T=\overline{k}\frac{\partial u}{\partial x}\mathrm{\Delta }x$$

where $\overline{k}$ is the spring constant for that small chunk of the spring. You may recall that the spring constant for a set of springs in series is the inverse of the sum of the inverses of the individual spring constants. Recognizing that our full spring is a bunch of spring chunks in series, and using the series formula in reverse, we can determine the spring constant of each little chunk:

$$\overline{k}=k\frac{L}{\mathrm{\Delta }x}$$

Therefore our relationship for the tension is, after canceling out the $\mathrm{\Delta }x$ terms,

$$T=kL\frac{\partial u}{\partial x}$$

Now for the dynamics. Newton’s Second Law, applied to the little chunk is

$$\sum F_x=(T+\frac{\partial T}{\partial x}\mathrm{\Delta }x)-T=\overline{m}\frac{{\partial }^{2}u}{\partial t^2}$$

where $\overline{m}$ is the mass of the chunk and ${\partial }^{2}u/\partial t^2$ is its acceleration. It should be clear that

$$\overline{m}=m\frac{\mathrm{\Delta }x}{L}$$

and therefore

$$\frac{\partial T}{\partial x}=\frac{m}{L}\frac{{\partial }^{2}u}{\partial t^2}$$

Since we already have an expression for $T$ from Hooke’s Law, we can differentiate it and substitute in to get

$$\frac{{\partial }^{2}u}{\partial t^2}=\frac{k{L}^2}{m}\frac{{\partial }^{2}u}{\partial x^2}$$

This is the governing partial differential equation for the longitudinal vibrations of the spring. It’s common to introduce a new variable, $c$, where

$$c^2=\frac{k{L}^2}{m}$$

to put the equation into a more compact form:

$$\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2}$$

As we’ll soon see, $c$ does more for us than just make the differential equation shorter. But first, because you’ve been so indulgent, a short break:

So often, I find, it’s the bloody binomial theorem. Now, back to work.

There are basically two ways to solve the differential equation: a modal approach and a wave approach. We’re going to take the wave approach.

The wave approach is based on a recognition that a general solution will take the form

$$u=f(x-ct)+g(x+ct)$$

where $f$ and $g$ are functions whose forms will depend on the initial and boundary conditions of the problem. But even without knowing the exact form of $f$ and $g$, we can say a lot about the solution.

Let’s look at $f$ by itself. Notice that

$$f(x-c{t}_2)=f([x-c(t_2-t_1)]-c{t}_1)$$

which means that $f$ at $t_2$ looks just like $f$ at $t_1$, except that it’s been translated $c(t_2-t_1)$ to the right. This is true regardless of the shape of $f$.

Thus, $f$ represents a wave traveling from left to right at a speed $c$.¹ It doesn’t change shape, it just keeps moving to the right until it gets to the right end of the spring. (What happens to it there depends on the boundary conditions at the right end and is something we’re not going to deal with in this post.)

We could go through the a similar argument for $g$—it represents a wave traveling from right to left. From now on, we’ll consider only cases for which $g=0$: waves traveling exclusively from left to right.

There’s an interesting relationship between the tension in the spring at a point and the velocity of that point. Since the displacement is

$$u=f(x-ct)$$

the velocity is

$$v=\frac{\partial u}{\partial t}=-c{f}^{\prime }(x-ct)$$

where

$$f^{\prime }(z)=\frac{df}{dz}$$

We can compare this to our formula for the tension,

$$T=kL\frac{\partial u}{\partial x}=kL{f}^{\prime }(x-ct)$$

and use a bit of algebra to get

$$T=-\frac{kL}{c}v=-\frac{mc}{L}v$$

So if the wave is moving to the right and the point on the spring is also moving to the right ($v>0$), the tension at that point is less than zero, which means the spring is in compression. This makes sense. If you give the left end of the spring a whack, the coils of the spring will shift to the right, the wave will move to the right, and the wave will be a compression wave because the coils will be getting closer to one another.

The other significant thing about this last equation is that the compression wave has the same shape as the velocity wave—the only difference is scale. And they both travel at the same speed, $c$, as the displacement wave.

It might be worthwhile to stop here and point out that the velocity of a point on the spring, $v$, is not the same as the wave speed, $c$. This is sometimes a source of confusion in longitudinal waves, because the points of the spring are moving in the same direction as the wave.

At this point, you may think I’ve forgotten about the slinky. No, we’re almost there.

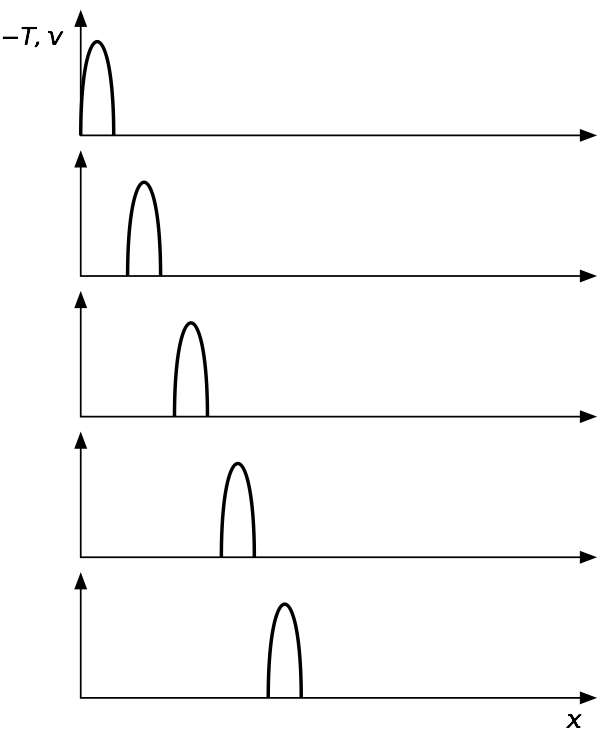
Consider what happens when our spring gets hit on the left end. The impact imparts a rightward (positive) velocity to the coils at that end, and those coils are compressed. Immediately after the impact, there is no compression anywhere in the spring except in those few coils at the left end. Because of the relationship between tension (or compression) and velocity, the only coils that are moving immediately after the impact are those same coils at the left end.

What happens from now on? The compression wave ($-T$), which looks like a short spike, travels along the spring at speed $c$. Here’s what it looks like in a series of snapshots:

Before the compression wave gets to a point on the spring, that point does not move, because there is only velocity where there is compression. After the compression wave passes a point, that point stops moving for the same reason.

You can test this yourself if you have a spring with a spring constant small enough to allow you to see the wave travel through it. Set the spring on a table and hit one end with a hammer. The spring will not move forward as one, its coils will inch ahead individually as the compression wave passes through them. When the compression wave reaches the other end of the spring—well, I said I wasn’t going to talk about that in this post.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang