Benchmarking password generation
August 29, 2010 at 2:16 PM by Dr. Drang
In my recent post on password cracking, I mentioned in passing that I thought the values in this table of password generation times were a little high. In today’s post I’ll show why I said that and also prove that I can program, albeit clumsily, in C.
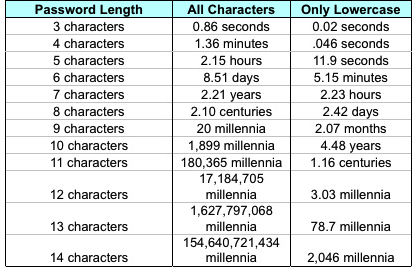
The table came from this LifeHacker article by John Pozadzides and purports to show how long it would take to generate all possible passwords of various lengths. Implicit in the table’s construction is the assumption that each password takes one one-millionth of a second to produce. Pozadzides says this represents what “an average computer” can do.
I thought that was a little slow, so I wrote this program to check it out.
1: #include <stdio.h>
2: char pw[] = "12345";
3: int i, j, k, l, m;
4:
5: int main(){
6: for (i=97; i<123; i++) {
7: pw[0] = i;
8: for (j=97; j<123; j++) {
9: pw[1] = j;
10: for (k=97; k<123; k++) {
11: pw[2] = k;
12: for (l=97; l<123; l++) {
13: pw[3] = l;
14: for (m=97; m<123; m++) {
15: pw[4] = m;
16: printf("%s\n", pw);
17: }
18: }
19: }
20: }
21: }
22: }
A few things to note about this program:
It’s written in C, a language I’ve actually taken a class in but haven’t programmed in in years. The logic of the program was a snap, and I’d even remembered the format for the
forloop (probably because of my years of Perl programming), but I’d forgotten a lot of the basics. Like how to declare a string and that a program needs amainfunction. Fortunately, this kind of information is just a short Google away.So why did I use a language I’m unused to? Because I didn’t want the overhead of an interpreted or semi-compiled language. A real password cracker would certainly be compiled.
- It’s written specifically to generate lowercase passwords five characters long. A more general program would probably use a recursive function, but I didn’t want to spend the time or effort to do that.
- It does print the generated passwords to standard output in Line 16. Omitting that line would make the program run faster, but I didn’t think that was a fair test, as the purpose of a password generator is create a list of passwords for later testing.
I compiled the program with gcc and then timed its run with the time utility. Here’s the session on my old 1.2 GHz PowerPC G4 iBook (the dollar sign is my Terminal prompt):
$ gcc -o lower5 lower5.c
$ time ./lower5 > pw5-c.txt
real 0m8.451s
user 0m3.206s
sys 0m0.998s
Now you see why I said Pozadzides’ numbers looked slow. Even a creaking, ancient, six year old machine can whip up a list of passwords in less time than his table says.
After writing the post, I compiled and ran the same program on my 2.16 GHz Intel Core 2 Duo iMac and got these timings:
real 0m1.666s
user 0m0.835s
sys 0m0.282s
This computer—which I consider to be my “new, fast” machine, even though it’s nearly four years old—generated passwords nearly an order of magnitude faster than the “average computer” of Pozadzides’ table.
None of this is meant to dispute Pozadzides’ main point, that longer and more complicated passwords are much harder to crack. Nor is it meant to suggest that passwords have become easy to crack with modern computers. Just don’t believe everything you read, and when you can easily check something out, you should.
