Next post Previous post

Hexagonal bundle math

January 13, 2017 at 10:43 PM by Dr. Drang

Today I ran across a fun little math problem based on the packing of circles into hexagons. I suspect Martin Gardner wrote a column about this 40–50 years ago, but I didn’t have access to that, so I had to work it out for myself.

The problem arose as I was looking at a shipment of small-diameter pipe. Manufacturers of round steel and aluminum products—pipe, conduit, round bars, and the like—often band their products together into hexagonal bundles before putting them onto trucks or flatcars for shipping. This makes for a compact shape in which the individual pipes are held together tightly and won’t slip out of the bundle.

Black Hexagon

I needed to check the calculated weights of some of these bundles, which meant knowing, among other things, the number of pipes in a bundle. It wouldn’t be terribly difficult to count, but I assumed there must be a formula for it. What was the formula, and how could I derive it?

A couple of ways came to mind, but the simpler was to consider the bundle as a series of concentric hexagonal rings around a central pipe. Apart from that central pipe, each ring contained successive multiples of six pipes. Adding all the rings together (and the central pipe) gets the total number. Here’s an example for a bundle with six pipes along the outer sides.

Colored Hexagon

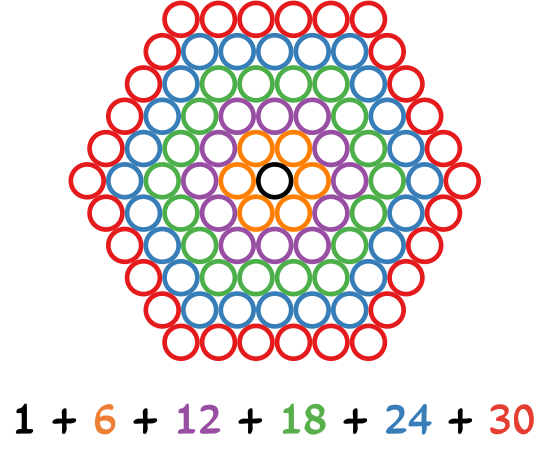
This would be easy to calculate—or to program—for any practical bundle size, but I wanted a formula, not an algorithm. Let’s take the number of pipes on a side to be nn. The total number of pipes in the bundle is then

1+∑i=2n6(i−1),forn≥21 + \sum_{i=2}^n \, 6\:(i - 1),\quad\quad \mathrm{for}\; n\geq2

We can pull the 6 out of the summation,

1+6∑i=2n(i−1)1 + 6\; \sum_{i=2}^n \,(i - 1)

and substitute in j=i−1j = i-1

1+6∑j=1n−1j1 + 6\; \sum_{j=1}^{n-1} \,j

The last term is the famous Gauss summation, for which we already have a formula. Plugging that in, we get

1+6(n−1)n21 + 6\; \frac{(n - 1)\; n}{2}

which we can reduce this down to the very simple

3n(n−1)+13\:n\:(n-1) + 1

So for the bundle above with six pipes per side, we get 91 pipes in the bundle. Five per side gives 61 pipes in the bundle, seven per side gives 127, and so on.

I’m sure the sales staff and shipping departments of pipe manufacturers know all these numbers for common bundle sizes. Now we do, too.

Next post Previous post