Kilometers, miles, Fibonacci, and Lucas
November 11, 2024 at 3:31 PM by Dr. Drang
Earlier this month, I got an email from Anthony SEROU about my post on the golden ratio and converting between miles and kilometers. They suggested using consecutive Fibonacci numbers as a quick way to do the conversion, e.g., 5 miles is 8 kilometers. And if the amount you’re converting from is one away from a Fibonacci number, you can add or subtract 0.6 or 1.6, depending on which way you’re converting. So 6 miles is about 9.6 kilometers and 7 kilometers is about 4.4 miles.
I had my doubts about the value of this until this weekend. I went out on a bike ride with a friend, and when we were about finished, I looked at my watch and saw that we’d gone 13 km. When I told him, and he asked “What’s that in miles?” I had the answer almost immediately because of Anthony’s email. I say “almost” because I spent fraction of a second being surprised that I actually had a Fibonacci number in front of me.
But my answer was fast enough to raise a question in my friend’s mind. He texted me later to say that I was right about it being 8 miles. I didn’t explain how I knew it so quickly—I have enough of a reputation as a oddball. Letting him think I could multiply quickly was easier than explaining Fibonacci numbers, the golden ratio, and the coincidence regarding the conversion between miles and kilometers.
Today it occurred to me that the ratio of consecutive Lucas numbers also converge to the golden ratio, so maybe they could be used the same way. So I fired up Wolfram and made a plot of the ratio of consecutive numbers against the larger of the two. In other words, I plotted y values of
against x values of for the Fibonacci numbers and similarly for the Lucas numbers. Here’s the result, where the golden ratio is the dashed black line:
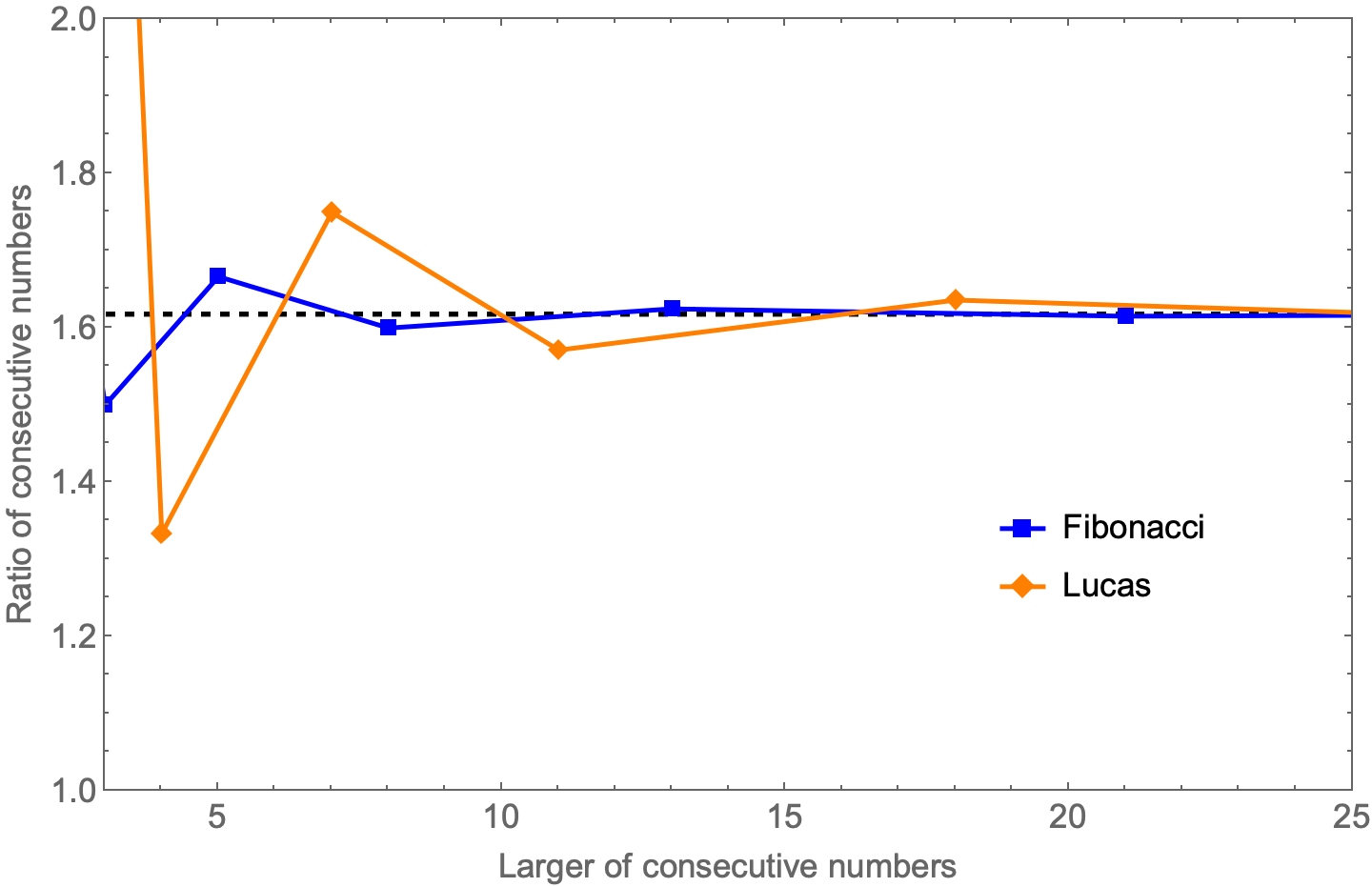
So while the Lucas number ratios converge to the golden ratio, they don’t do so as quickly as the Fibonacci numbers. Just as well. Only real oddballs know the Lucas numbers.
