Next post Previous post

The Antikythera mechanism

December 15, 2024 at 9:45 AM by Dr. Drang

A recent episode of the In Our Time podcast is about the Antikythera mechanism, which you’ve probably heard of. It’s a bronze device that dates back to the first century BCE and was found by divers on an ancient shipwreck off the Greek island of Antikythera in the early 1900s. It’s main purpose, as determined by slow study over the past hundred years, was to track the positions of the “planets,” which in its time were the Sun, Moon, Mercury, Venus, Mars, Jupiter, and Saturn.

The show is very good, covering both the mechanism itself and the development of what’s known about it. There’s also some fun speculation on who made it and who owned it. This post expands on a couple of numerical/astronomical/calendrical things mentioned by the guests.

At about the 32-minute mark, Mike Edmunds talks about a large wheel in the mechanism that has, he says, 233 teeth, equal to the number of lunar months in the Saros cycle, which is used to predict eclipses. I mention it here for two reasons:

First, Prof. Edmunds misspoke slightly. The Saros cycle is 223 lunar months, not 233. And it’s worth mentioning that what I’m calling a lunar month is also known as a synodic month and a lunation, depending on which reference you’re looking at. It’s the time between one new moon and the next,1 which is about 29½ days

Second, so you could see the spelling of Saros in case you wanted to do your own searching on the topic. If so, I recommend this article by Fred Espenak on NASA’s website. It includes two other month definitions, anomalistic and draconic.

Earlier in the show, at about the 14-minute mark, Jo Marchant talked about a particular gear train in the mechanism, in which

the first six gear wheels… convert the speed by a ratio of 254 over 19, which… harmonizes the motion of the Sun and the Moon.

I was out on a walk as I first listened to the episode, and I misheard this part. I thought she said 354 instead of 254. So my instinct was that the 19 came from the length, in years, of the Metonic cycle and that the 354 came from the number of days in 12 lunar months (12×29.5=354). I knew that the Metonic cycle was the period it took for a lunar calendar and a solar calendar to get back in sync,2 but I didn’t understand what that had to do with the number of days in 12 lunar months.

When I got home and listened to that chunk of the show again, I realized that I had misheard, but hearing it right led to another question. The Metonic cycle is 19 years or 235 lunar months—where does the 254 come from?

After some thinking, I realized that although there are 235 lunar months in a Metonic cycle, that’s not how many times the Moon orbits the Earth in 19 years. A new moon occurs when the Moon is directly between the Sun and Earth. Because the Earth has gone nearly 30° around the Sun in one lunar month, that means the Moon has gone nearly 390° around the Earth in that time. Over the course of a year, the Moon has made one more orbit of the Earth than you would think if you just divided the number of days in a year (365.2421881) by the number of days in a lunar month (29.53058891).

If you’re used to thinking in terms of sidereal time, or if you watched this Veritasium video on a screwed-up SAT question, you know that if there are 235 lunar months and 19 years in a Metonic cycle, the Moon must have orbited the Earth 235+19=254 times. Therefore, the number of Moon orbits and the number of Earth orbits must be in a ratio of 254:19.

If this still is still puzzling, a picture might help. Here are the Sun, Earth and Moon at two successive new moons, as viewed from “above” the solar system.

Sun-Earth-Moon movement over a lunar month

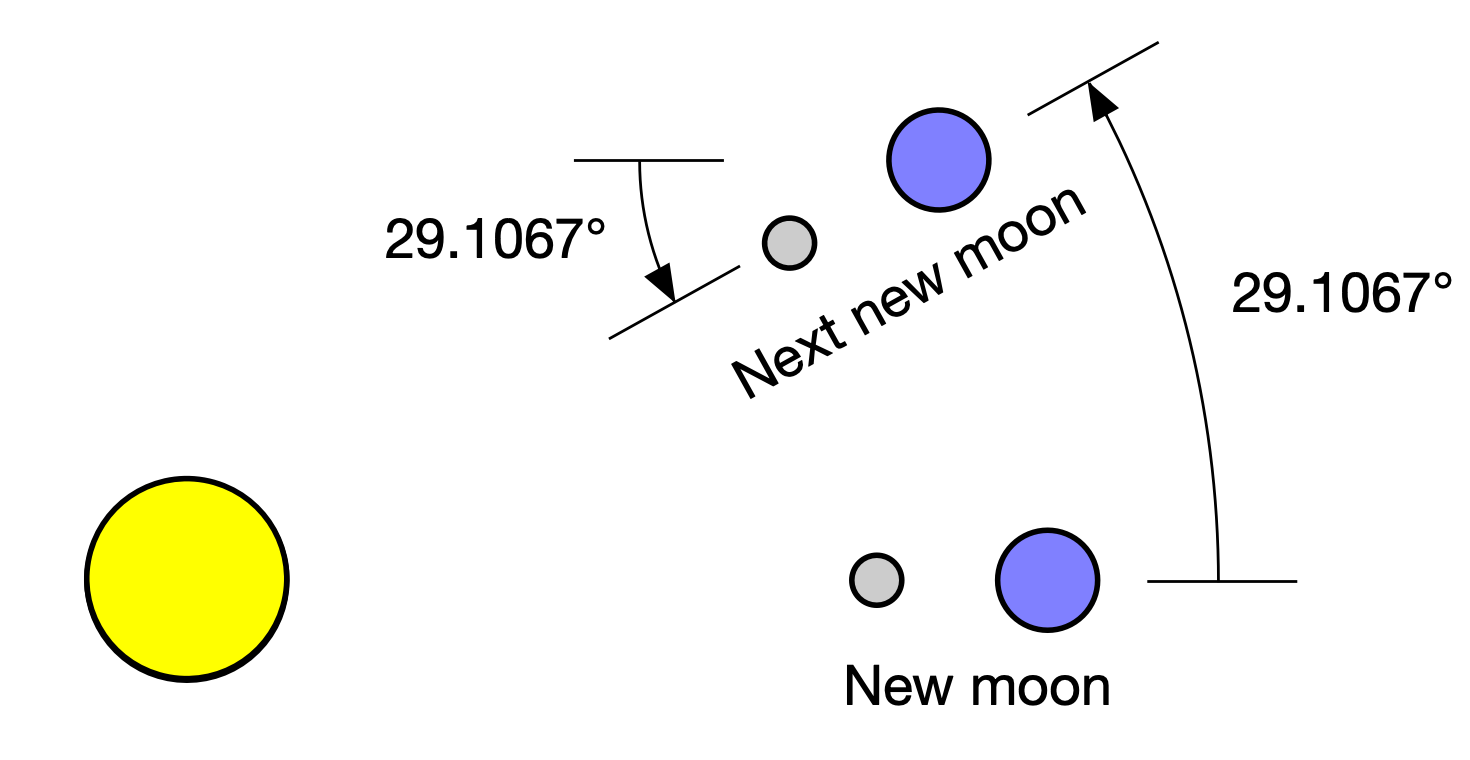
The angle that the Earth goes through in one lunar month is

29.53058891365.2421881360 ∘=29.1067 ∘

During that time the Moon goes around the Earth one full orbit plus that amount, or

360 ∘+29.1067 ∘=389.1067 ∘

So the ratio of the Moon’s angular speed3 to the Earth’s is

389.106729.1067=13.3683

And over 19 years, the Moon goes through

19×13.3683=253.997≈254

orbits of the Earth. And this is where the 254:19 ratio comes from.

I can think of three objections to this calculation. Let’s go through them.

Elliptical orbits
Implicit in the calculation is that the orbits of the Earth and Moon are circular. This isn’t true, but it’s pretty close. The Earth’s orbital eccentricity is just 0.0167 and the Moon’s is 0.0549. More important, the angle calculations are averages; even though the Earth speeds up and slows down over the course of a year, its average angular movement is 29.1067° over an (average) lunar month.

Sidereal vs tropical year
You may have noticed that I used the length of the tropical year in the calculation. If I’m going to compare the motions of the Earth and Moon relative to the fixed stars, shouldn’t I be using the sidereal year of 365.25636 days? Strictly speaking, yes, but when the Antikythera mechanism was built the precession of the equinoxes had been known for only a century or so and may not have been known to the devices makers. It certainly wasn’t built into the Metonic cycle, which predated the discovery of precession by centuries. But even if I had used the sidereal year, the calculation would have been

29.53058891365.25636360 ∘=29.1056 ∘ 360+29.105629.1056×19=254.006

which is still very close to 254. The precession adjustment is only about 1 part in 26,000.

Heliocentric motion
My sketch of the Sun-Earth-Moon system assumes a heliocentric solar system, something that wasn’t known to the Greeks of the first century BCE. In the podcast, Mike Edmunds says Greek philosophers of that time would have been open to the idea of heliocentric motion, but that’s a far cry from taking it as a given. But while the Greeks may not have known the reason for the Metonic cycle, they still knew it as an empirical fact, based on centuries of observations. Whatever caused the Moon and Sun to move across the sky as they did, they moved in a ratio of 254:19.

I’ve always liked blogging about calendrical things, but I don’t remember doing anything on the Metonic cycle before. If I had written faster, I could’ve published it on Friday the 13th. Too bad.

  1. Or one full moon and the next; the period is the same either way you look at it. ↩

  2. For example, there was a new moon a couple of weeks ago, on December 1, 2024. The next time there will be a new moon on December 1 will be in 2043. This is for Chicago, by the way; these new moons could be one day off in different parts of the world. The Metonic cycle was named after Meton of Athens, who lived in the fifth century BCE, and was well known in the Greek world. ↩

  3. Here I’m talking about the circular motion of their centers. This has nothing to do with rotation about their axes. ↩

Next post Previous post