House of cards redux
January 18, 2025 at 2:46 PM by Dr. Drang
You may remember this post from back in October. It’s about a puzzle in the November issue of Scientific American in which the goal was to determine if you could build a house of cards of the following design with exactly 100 cards. And if so, how many stories would the house have?
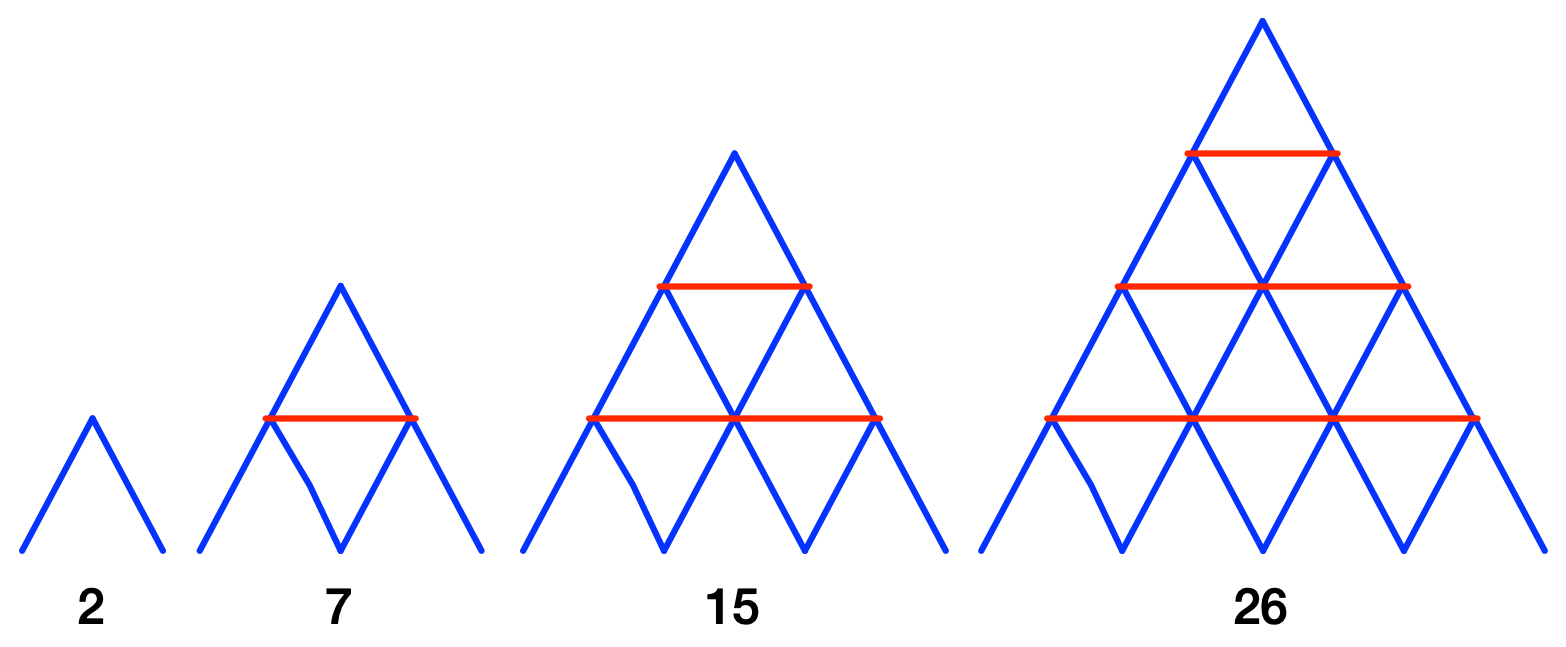
The answer was yes, an 8-story house built this way would have 100 cards. My solution hinged on the recognition that the numbers of cards for increasing story count is related to triangular numbers. I got the answer by using the equation for triangular numbers and the quadratic formula.
The folks at SciAm went about it a different way. They set up a table of story counts and card counts and took the first and second differences of the card counts. Like this:
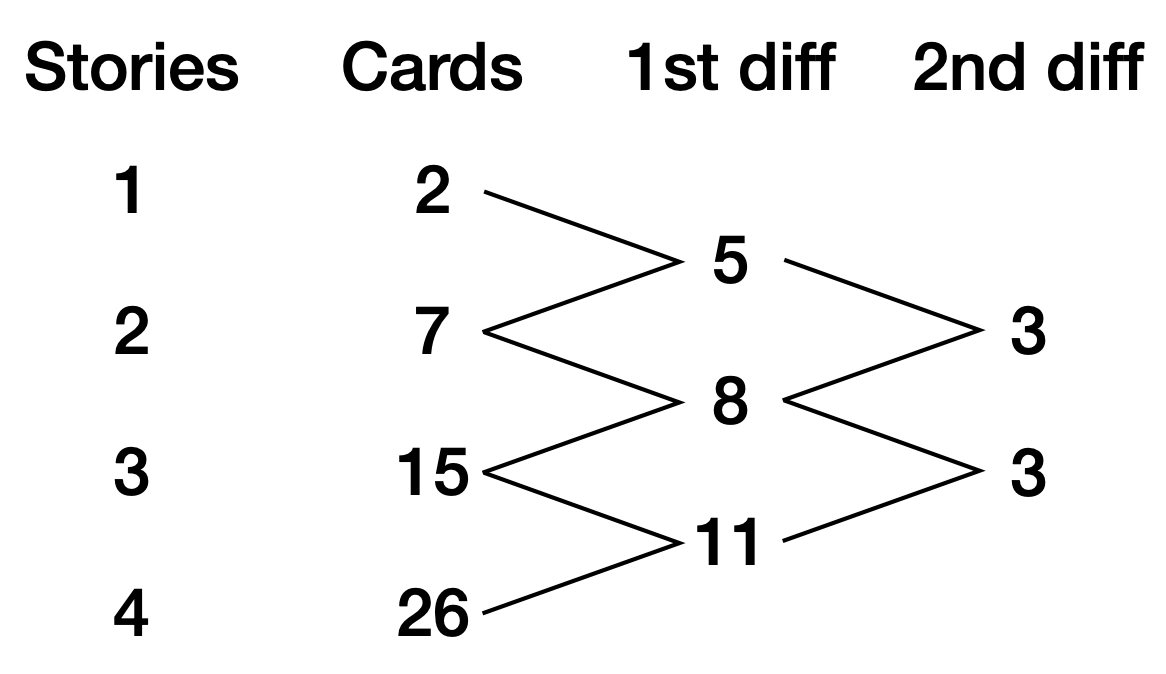
They reasoned that since the second differences were constant, the formula for the card count must be of the 2nd degree. They then determined the three coefficients of that 2nd degree formula via simultaneous equations.
At the end of the post, I said that although I preferred my solution, I wanted to learn more about difference tables. About a month ago, I was in a bookstore and saw J.F. Steffensen’s Interpolation on the shelf. Difference tables play a big role in the book, so I bought it. It helped that it’s a Dover reprint, so it was inexpensive.
I’ve been skimming the book to figure out which parts I want to dig into and found a really simple way to solve the house of cards puzzle with no algebra whatsoever. Start by building the difference table as SciAm did it. Then recognize that the constancy of the 2nd difference column lets you extend the table to whatever length you want.
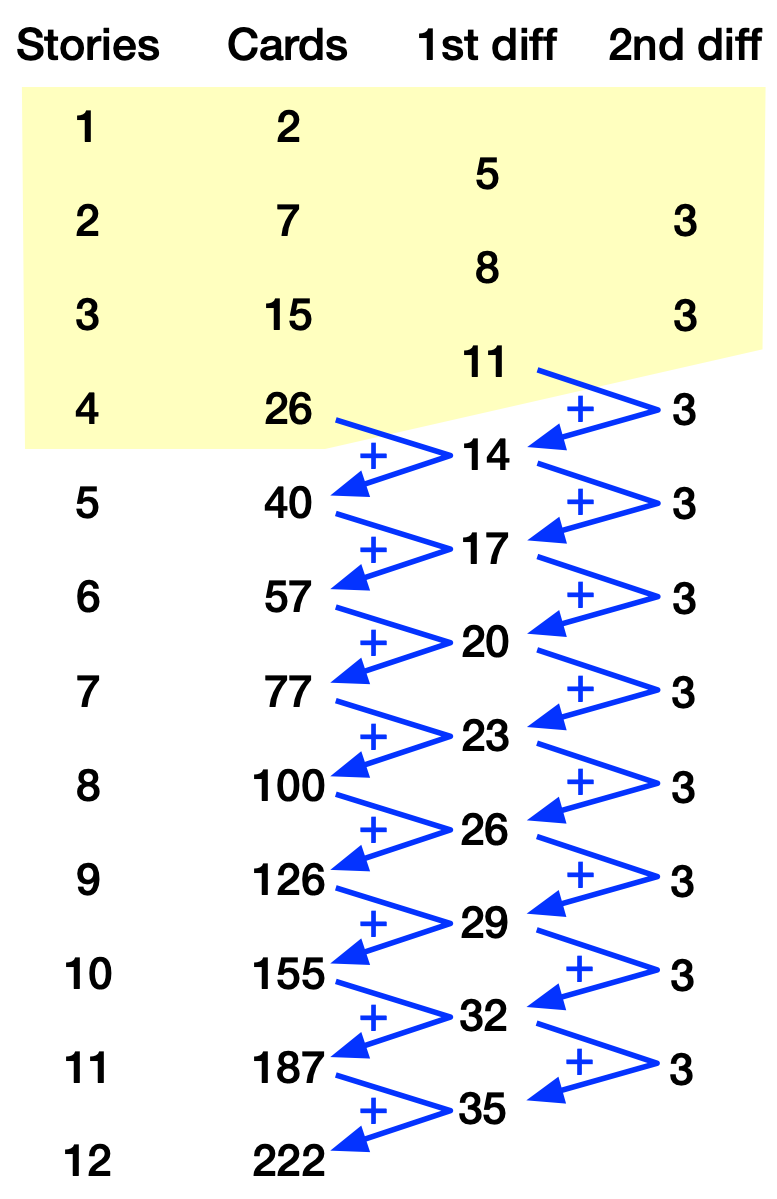
The part with the yellow background is the part of the table we did before. Since the 2nd difference column is constant, we can just write 3’s for every entry. Then we work backwards to fill in the rest. We extend the 1st difference column by adding 3 (the 2nd difference value) to each preceding value:
Then we fill in the Cards column by adding the 1st difference values to the preceding card count:
That 100 corresponds to Row 8 of the table, so an 8-story house of cards has 100 cards. I went further than was necessary to solve the puzzle just to show how easy it is. The numbers were small enough that I could do all the addition in my head.
It’s true that having a formula allows you to get the card count directly for any number of stories, while using the difference table this way forces you to calculate all the intermediate values. In general, it’s better to have the formula. But for this specific puzzle, the difference table is faster.
