Factors of safety
March 28, 2025 at 5:04 PM by Dr. Drang
In an update to the phone bending post, I used the term “factor of safety.” It’s a simple and seemingly self-explanatory phrase, but there’s a lot of depth to it. This post discusses how it’s used—and not used—by structural and mechanical engineers.
What is a factor of safety?
At it’s simplest, a factor of safety is the ratio of strength to load. Let’s say we have a wire rope with a diameter of 1″ and we use it to suspend a load of 20,000 lbs. A common rope of that size (its length doesn’t matter) has a strength of 103,400 lbs (given as 51.7 tons in this table), so its factor of safety is
Note that the load and strength values are given in the same units, so the factor of safety is a pure number. If we converted the values to SI units, the factor of safety wouldn’t change. So if you were specifying a minimum factor of safety for some mechanical or structural component, you’d use the same value whether the design is being done in SI or US customary units. We’ll talk later about how factors of safety are chosen.
A load hanging from a wire rope is an especially simple structure. There’s basically one way for it to fail, so there’s only one factor of safety we need to calculate. Most engineering systems, even those that might seem equally simple, can fail in several ways—we call these ways the modes of failure—and we have to calculate factors of safety for all of those modes.
For example, let’s say we have a horizontal beam carrying a vertical load. Here are its potential modes of failure:
- Plastic deformation. This is bending to the point where the beam doesn’t spring back when the load is removed.
- Lateral-torsional buckling. This is moving sideways and rotating, a mode of failure that is particularly significant in tall skinny beams.
- Local buckling. If certain parts of a beam are long and thin, the beam’s capacity can be limited by their buckling even though the beam as a whole doesn’t buckle.
- Connection failure. These might be end connections, where the beam attaches to columns; or they might be internal connections, where parts of the beam attach to other parts. Any of these connections could be made of bolts, welds, or a combination of bolts and welds. The bolts could break, the welds could break, the metal around the bolt holes could tear—there are lots of ways connections can fail.
All of these modes of failure have to be investigated, and they all have their own factor of safety.
Why do we need factors of safety?
If we know that the strength of a component is greater than the load that will be applied to it, why do we need any factor of safety at all? Why specify any factor of safety greater than 1? The key is the word “know.” How can we know the maximum load that will be applied to a component over its time in service? Engineers aren’t issued crystal balls along with their diplomas. And even though it’s very nice for wire rope manufacturers to put the breaking strength of their products in a table, aren’t there tolerances on the strength of the steel and the diameters of the individual wires? Even more important, don’t wire ropes accumulate damage during service, and doesn’t that reduce their strength?
Questions like this point out the uncertainty designers have in both the strength of their designs and the loads that will be applied to them. It is this uncertainty that leads to factors of safety. Some writers refer to the factor of safety as the “factor of ignorance” to emphasize the uncertainty.
We do try to get a handle on this uncertainty. On the load side, we can sometimes make good estimates of the load through calculation. A water tank, for example, can only hold as much water as its volume will allow, and since we know the density of water quite well, we can make a pretty accurate estimate of the maximum vertical load that water tank will experience. But what about the floor loads on an office? Should we assume that it’s crammed with people? Or stacked with paper from floor to ceiling? The latter would lead us to design floor beams that never break, but no one would pay to build such a building.
It turns out that these things have been studied, and there are ways to choose appropriate design loads for different situations. The American Society of Civil Engineers publishes a standard, ASCE 7, Minimum Design Loads and Associated Criteria for Buildings and Other Structures, that provides guidance (guidance that’s commonly mandated in building codes) on the loading you should use when designing various building components. Here’s an excerpt from the table that covers floor loading:
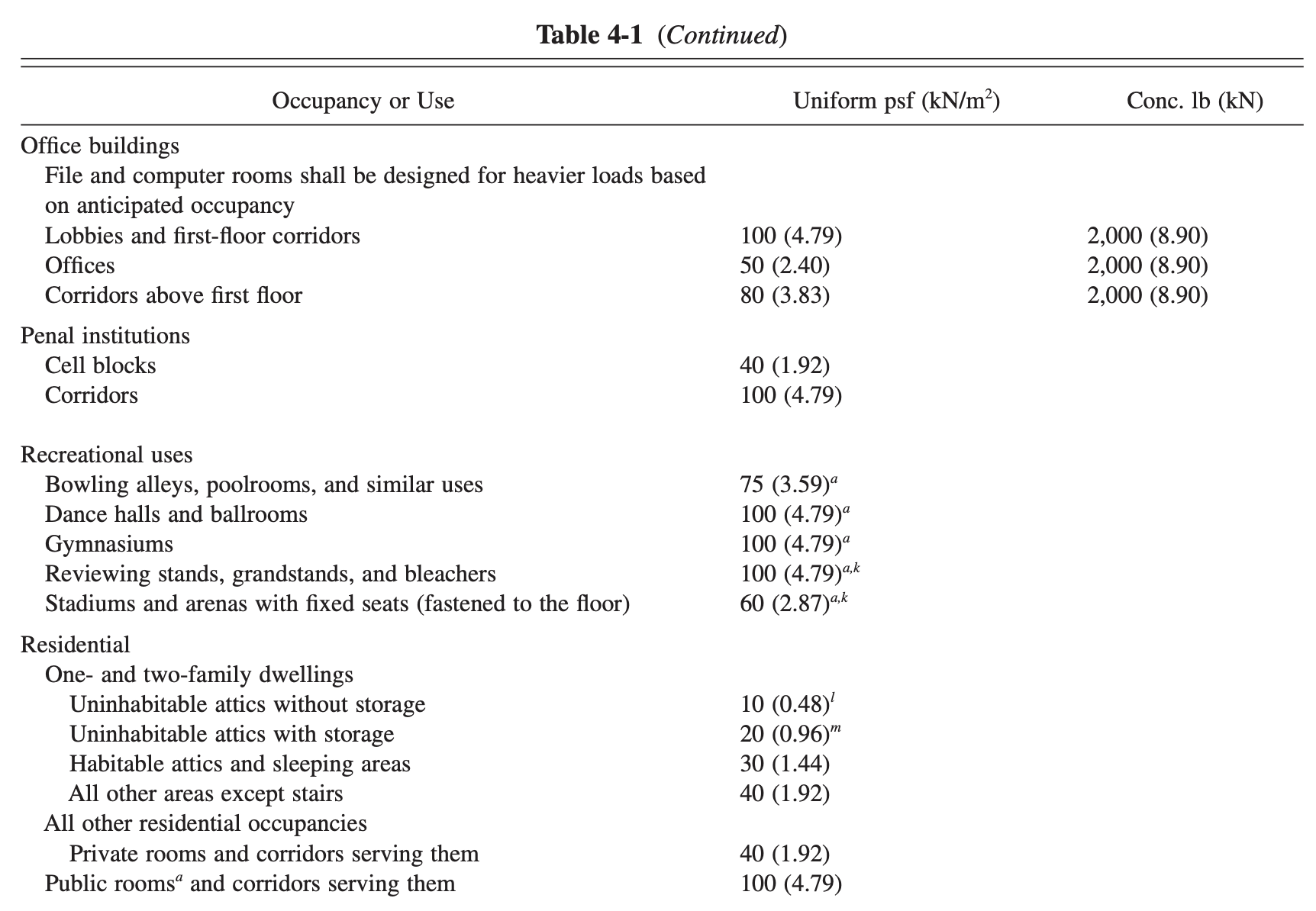
This doesn’t mean that you’ll never find an office with a load of more than 50 pounds per square foot. It means that that’s a good value to use when combined with other recommendations (which we’ll talk about later) in the standard.
On the strength side, we’ve already discussed how manufacturing tolerances lead to uncertainty. There’s also uncertainty that comes from us. Determining the strength of a component is usually not as simple as just looking up a number in a table. Most of the time, we have to create a mathematical model of the component’s behavior to calculate its strength. These models necessarily simplify the behavior and therefore have some uncertainty in them. Some models are quite accurate; others less so.
Conceptually, the uncertainty on the load and strength sides can be thought of like this:
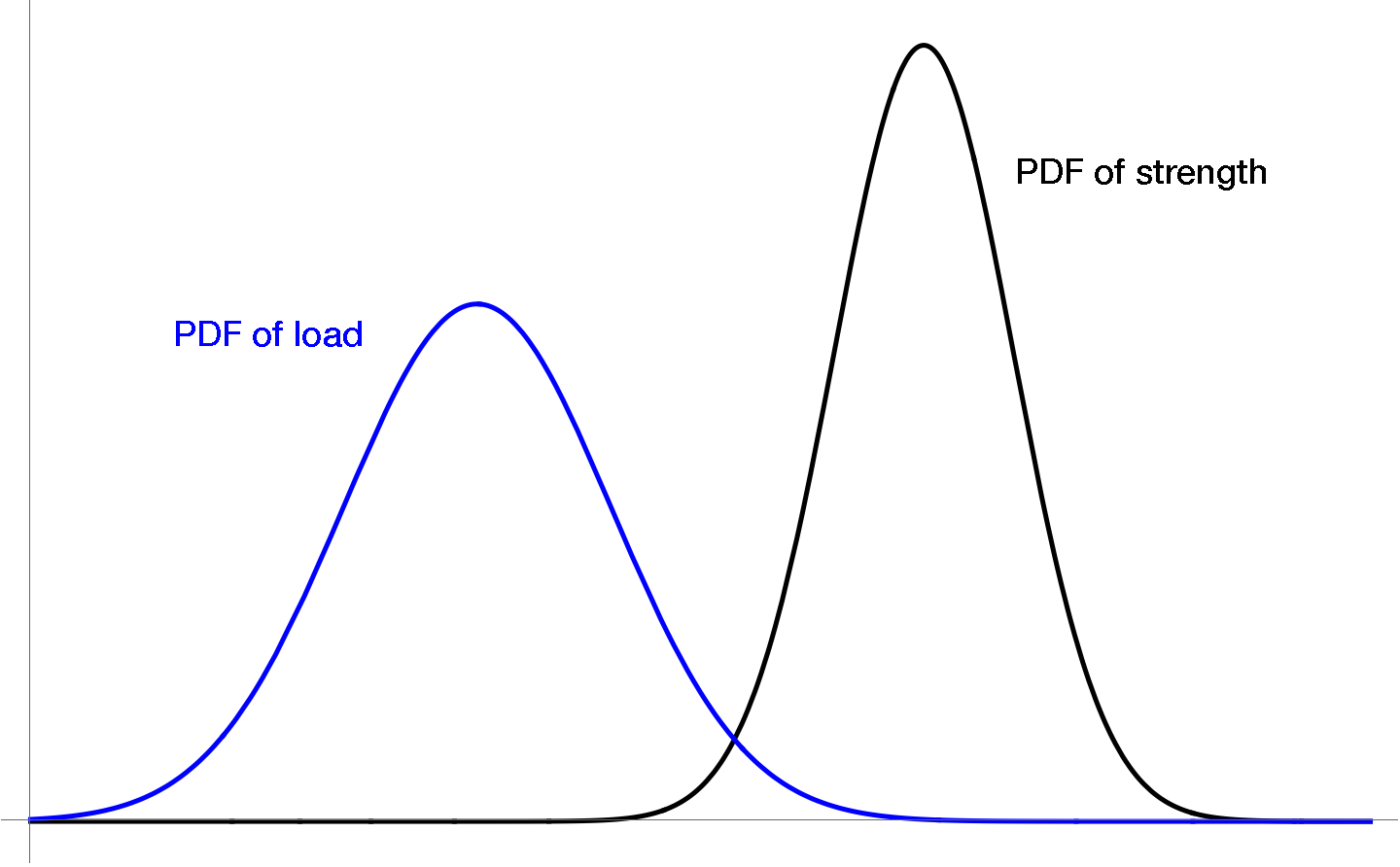
These curves are the probability density functions of the strength and load. They plot the relative likelihood of the component having a certain value of strength and being subjected to a certain value of load. The chance that load will exceed the strength is related to the amount of overlap between these two curves.
The more uncertainty there is in the strength or the load, the broader the associated curve will be.
Typically, there’s less uncertainty in the strength than the load, which is why I’ve drawn the black curve tighter than the blue curve. But if you think about the water tank example, that’s a situation where small uncertainty in the maximum load would make the blue curve pretty narrow. And if the strength curve is the same as it would be for any other structure, we could lower the factor of safety, i.e., scoot the two narrow curves closer to one another, and still achieve an acceptable level of safety.
How do we choose factors of safety?
For most of history, the answer to this question was “experience.” Many people would add “engineering judgment,” but judgment comes with experience, so I don’t see the need to clutter things up.
Sometimes the experience is successful. “We’ve been doing it this way for years, and it’s worked” is a pretty good argument for sticking with the factor of safety you’ve been using. On the other hand, sometimes success leads people to think that past designs have been too conservative—maybe we can shave the factor of safety down a bit and maintain the success we’ve been having. The people who write codes and standards are always weighing these opposing views.
Unsuccessful experience is more memorable, especially when modes of failure that were previously unknown take over. The Tacoma Narrows bridge collapse is perhaps the most famous example of engineers missing a mode of failure because they didn’t understand the load. The brittle fracture of Liberty ships is a prime example of a mode of failure that took over because engineers didn’t understand a certain type of strength. These were not failures of particular engineers; they were failures of the entire profession as new types of structure were being built.
Starting in the 60s, and with increasing speed in the 70s and 80s, structural engineers began making explicit the ideas that are implicit in the graph of the overlapping probability density functions. If they could measure the uncertainties in the loads and strengths, they could estimate the probabilities of various modes of failure
An important consequence of this approach to design was that factors of safety were split in two. Structural engineers now use “load factors,” which are based on the uncertainty in the applied loading (the width of the blue curve); and “resistance factors,” which are based on the uncertainties in the structural properties that govern strength (the width of the black curve). This split makes sense because load and strength are independent of one another. It’s more reasonable to use factors aligned to each type of uncertainty.
The ASCE 7 standard mentioned above includes not only the design values for various types of loading (like office floor loads), it also include the load factors that are meant to be used along with them. So floor loads, which are classified as live loads because they can change, are typically multiplied by a load factor of 1.6. By contrast, the weight of the structure itself—along with nonstructural components like drywall and floor tiling—is classified as a dead load because it doesn’t change, and it’s typically multiplied by a load factor of 1.2. This difference is due to the smaller uncertainty associated with dead loads compared to live loads.
The resistance factors are specified in other standards, standards that focus on the calculation of strengths. For steel structures, the American Institute of Steel Construction publishes AISC 360, the Specification for Structural Steel Buildings. In AISC 360, you’ll find that the basic resistance factor for bending is 0.90.
Note that this value is closer to 1 than the load factors. This is an example of what I said earlier; we tend to have less uncertainty about strengths than we do about loads.
Despite this advance by the structural engineering profession, the simpler idea of factor of safety hasn’t died. Mechanical engineers still tend to use factors of safety, probably because they have to deal with much more varied types of loading, loading for which the uncertainty is harder to measure. (Mechanical engineers do have the advantage that they can run extensive tests on prototypes of their designs. You don’t often see a prototype building being constructed and tested to destruction before erecting the “real” building.)
Is there any more?
Of course there is. In addition to the probability of failure, engineers also have to consider the consequences of failure. For example, it’s considered acceptable for the leads in mechanical pencils to break under reasonably foreseeable circumstances. Everyone who uses mechanical pencils has broken a lead by extending it too far or pressing too hard. We accept this because the consequences are minimal. We don’t allow automobile tires to burst with same probability that pencil leads break because the consequences are far more serious.
Risk is the combination of failure probability with failure consequences. The mathematics of risk is interesting, but I don’t think it has a lot of practical use right now. In particular, it’s hard to measure consequences. Economic losses are one thing, but injuries and deaths are quite different. It’s true that insurance companies and juries in product liability court cases put dollar values on injury and death, but no one likes it.
Finally
My Ph.D. research was on methods of calculating structural reliability, so I may have gone a little overboard here. But consider yourself lucky. The post I’ve been writing in my head over the past week was way longer.
-
Building codes typically have provisions that allow the designer to ignore certain modes of failure when the dimensions (the thickness of a flange, for example) meet some set of criteria. But even in these situations, factors of safety have been calculated; it’s just that the calculations have been done by the code writers, who have established that certain modes of failure are no longer possible if the criteria are met. ↩
-
I’ve drawn these as bell-shaped curves because people are used to seeing that kind of density function. In practice, they might have quite a different shape. ↩
-
To truly calculate the probability of failure requires more information on the PDFs of the load and strength than is typically available. But some measure of the failure probability can be estimated using the mean and variance of both the load and strength. ↩