Next post Previous post

Plastic bottles and pressure vessels

April 19, 2025 at 9:52 PM by Dr. Drang

Bill Hammack (The Engineer Guy on YouTube) had a nice video last week on the engineering behind plastic soda bottles. It’s well worth your 13 minutes.

Prof. Hammack is a chemical engineer, so you should pay particular attention when his topic is plastic. About 3:30 into the video, he talks about how, during the expansion of the bottle from its original size and shape (the preform), the long chain PET molecules tend to untangle and align themselves in the axial and hoop directions. This strengthens the bottle in those directions and makes it better able to handle the internal pressure.

Video frame showing polymer alignment

Why do these directions matter? Because they’re the directions of principal stress in the bottle’s wall, and the hoop direction is where you’ll find the maximum tension. This is one of the elementary bits of stress analysis you’ll find in an undergraduate mechanics of materials class. Not specifically for soda bottles, but for pressure vessels in general.

Here’s a typical cylindrical pressure vessel. The end caps—which I’ve made ellipsoidal because that’s relatively easy to do in Mathematica—don’t match what we see in soda bottles, but that’s OK. When you’re interested in the stresses in the vessel’s midsection, the shapes of the end caps don’t matter.

1

Pressure vessel

Something that does matter is the thickness of the wall relative to the radius. The analysis below is for thin-walled pressure vessels, which means that t≪r, where t and r are the wall thickness and cylinder radius, respectively.

You might be wondering “which radius?” There’s an internal radius and an external radius. Which one is r? For all practical purposes, it doesn’t matter because the internal and external radiuses are nearly the same, since

ro=ri+t=ri(1+ t ri ) ≈ ri

If the ambiguity bothers you, you can say r is the average radius.

We’re also going to assume that the pressure in the vessel is much larger than the hydrostatic pressure due to the weight of the fluid alone. That way, we don’t have to worry about the pressure being higher at the bottom of the vessel than at the top. This is certainly true in a soda bottle. Prof. Hammack says the pressure has to be about 70 psi to dissolve the CO2 in the liquid. The additional pressure at the bottom of the bottle due to the weight of the soda is only about 0.4 psi, so it’s reasonable to ignore it.

2

One last assumption: the stresses in the wall are constant from the inner surface to the outer surface. You might think of this as the wall being too thin for the stresses to have room to change. If you’re skeptical, I can tell you that more advanced analysis shows that the stress is indeed nearly constant across the wall thickness.

Let’s get to analyzin’. We’ll start by passing a plane through the bottle at right angles to its axis, and consider the free body diagram of the vessel and its contents on one side of that plane.

Axial stress FBD

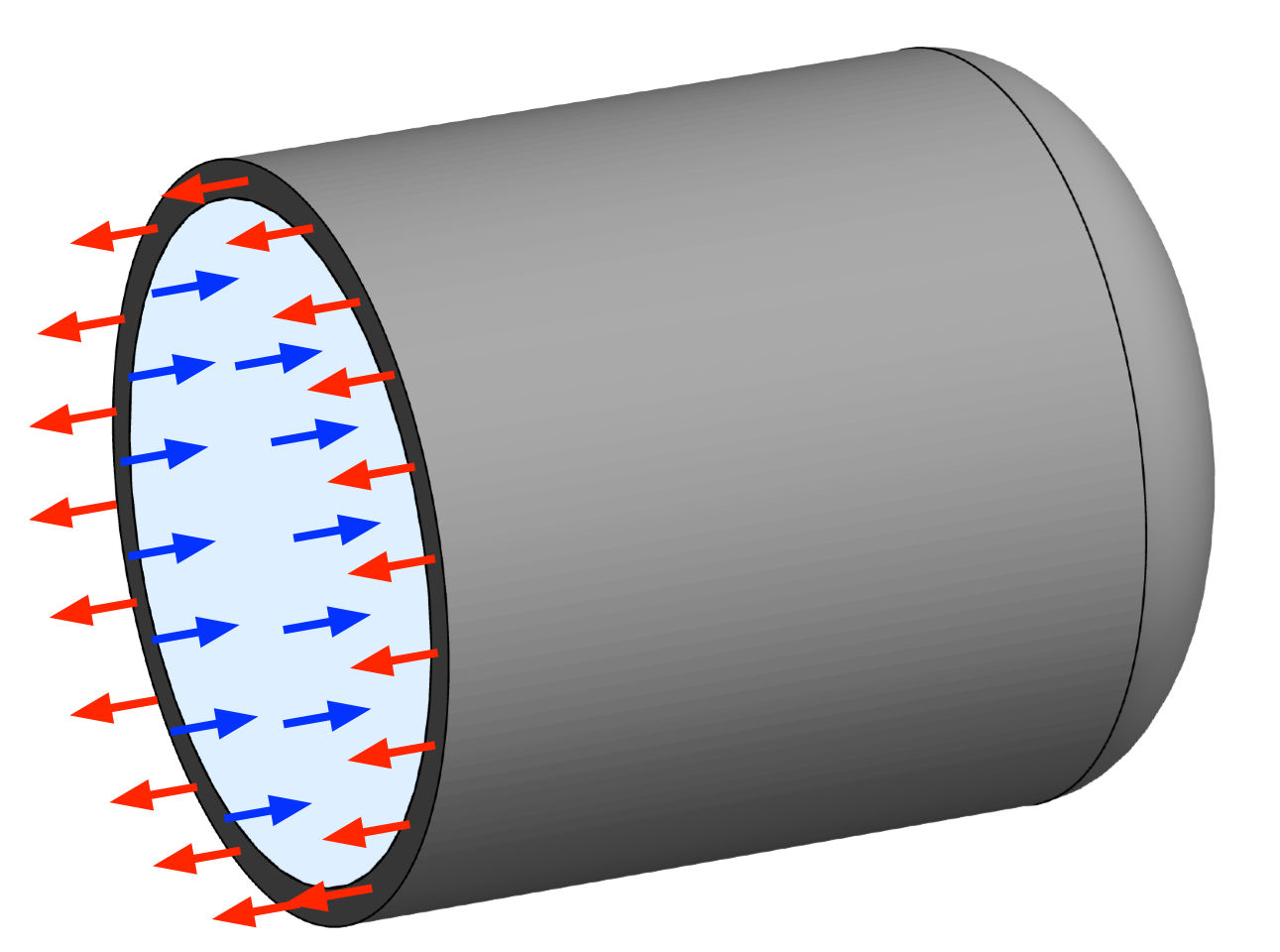
The red arrows represent the axial tension, σa, in the wall of the vessel, and the blue arrows represent the pressure, p, in the bottle. There are no shear stresses in the fluid because fluid’s don’t carry shear stresses when they’re not flowing, and there are no shear stresses in the wall because of the vessel’s symmetry.

Balancing the forces in the axial direction gives us

σa(2πrt)=p(πr2)

which simplifies to

σa= pr 2t

Now we make a new free body diagram by passing two parallel planes a distance w apart through the vessel perpendicular to its axis. Then we pass another plane that runs along the axis and consider the wall and fluid on one side of that plane.

Hoop stress FBD

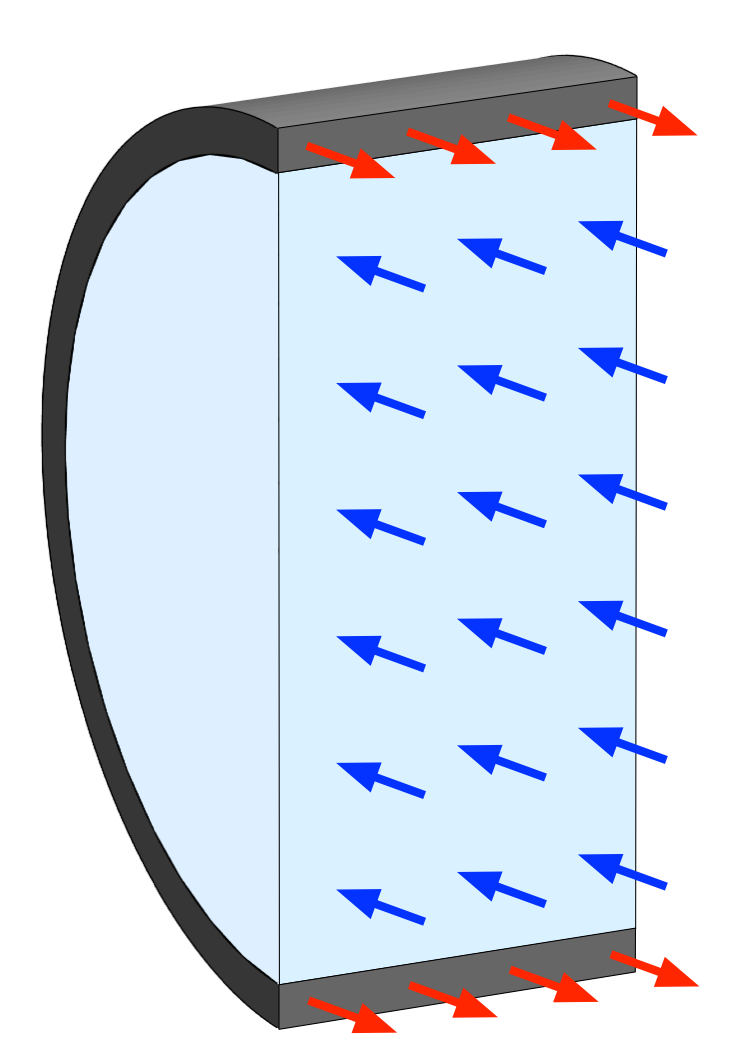
Because we’ve already analyzed the forces in the axial direction, and because they don’t affect equilibrium at right angles to them, I’ve left them out of this drawing. The balance of forces here gives

σh (2tw) = p(2rw)

which simplifies to

σh= pr t

So the tension in the hoop direction is twice the tension in the axial direction. But note that because t≪r, both stresses are much larger than the pressure in the vessel.

I don’t have any 2-liter bottles around the house, but I cut open a can of LaCroix (also a pressure vessel), and measured its diameter

3 at 66 mm and its wall thickness near the center at 0.10 mm. That means r/t=330. So the hoop stress in that can would be more than two orders of magnitude greater than the pressure in the fluid.

If the material the vessel is made from has the same strength properties in both directions, the hoop stress is the one you have to worry about. In plastic soda bottles, though, you probably have to worry about both stresses because the extent of molecule alignment is not necessarily the same in both directions. If that’s the case, the strengths in the two directions will be different, and you have to compare each stress with its corresponding strength.

  1. This is due to a phenomenon known as Saint-Venant’s principle, and it’s a good thing. If we had to account for the shapes of the end caps—which we do when calculating stresses in and near the end caps—the analysis would be considerably more complicated and we wouldn’t be teaching it at the undergraduate level. ↩

  2. He doesn’t say it, but I’m pretty sure that 70 psi is the absolute pressure. The gage pressure—the difference between the pressures inside and outside the bottle—is therefore about 55 psi. Still very large compared to 0.4 psi. In the analysis below, p is the gage pressure. ↩

  3. Nobody measures radius directly. You measure diameter and divide by two. ↩

Next post Previous post