Next post Previous post

Claude tries beam bending

July 26, 2025 at 7:15 PM by Dr. Drang

Leon Cowle asked Claude Sonnet to solve the same beam bending problem that I recently asked ChatGPT to solve, and he sent me Claude’s answers. Like ChatGPT, Claude started off giving the correct answer, but fell down when trying to explain it. What surprised me was the differences and similarities in their wrong explanations.

Claude’s initial answer for the tip deflection of this cantilever beam,

Cantilever beam with load at center

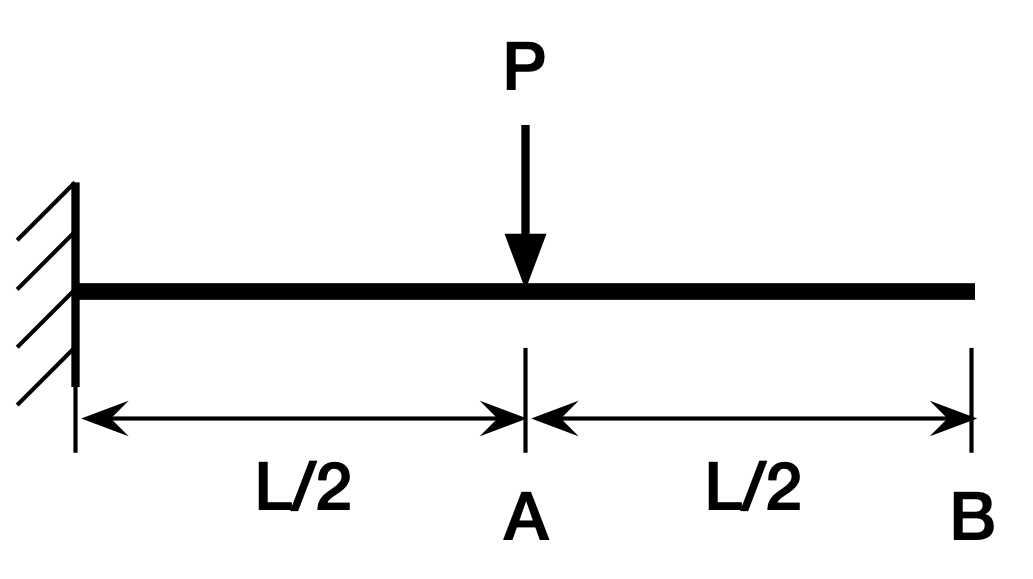
was correct:

δB=5PL248EI

At the end of its initial answer it said

The factor 5/48 comes from the integration of the moment diagram over the length of the beam, accounting for the specific loading condition at the midpoint.

which is an invitation to ask it to explain the solution. When Leon did, Claude’s first sentence was a disclaimer:

I need to correct my previous answer - I made an error. Let me work through the proper derivation.

Since the previous answer was correct, this tells us to be on the lookout for mistakes in the derivation.

(And I should also mention here that Leon is using a free account, so it’s possible that the other models or “extended thinking” available through a paid account would do a better job. Still, as I said about my use of ChatGPT, what is the inducement to pay when what you see for free is error-prone?)

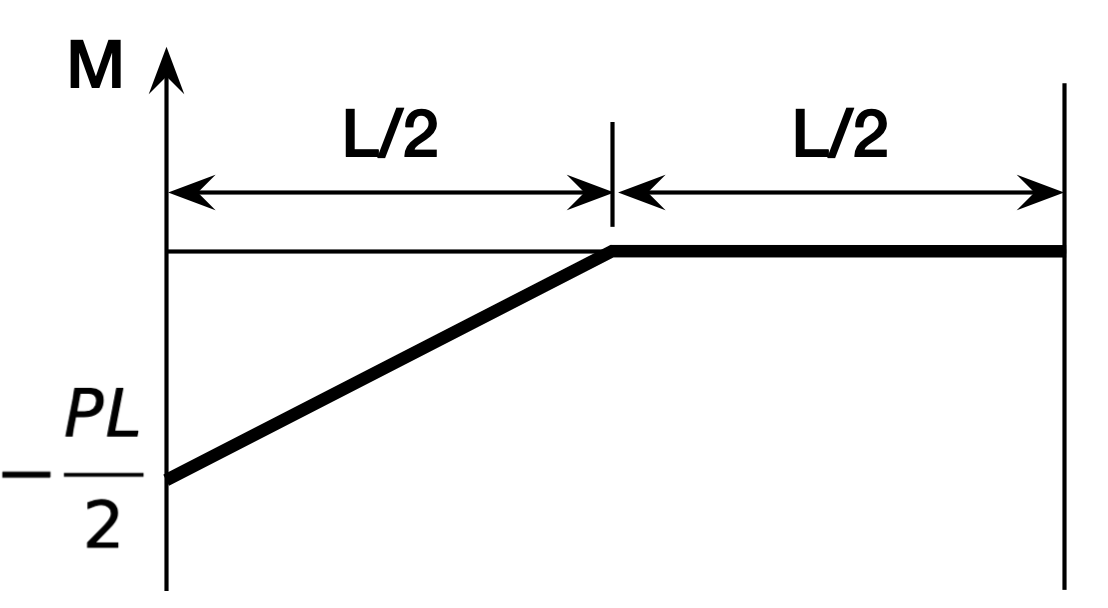
Unlike ChatGPT, Claude starts its derivation with correct equations for the bending moment in the beam. In the left half, 0≤x≤L/2,

M1(x)=−P(L2−x)

and in the right half, L/2≤x≤L,

M2(x)=0

This is correct, so Claude did a better job at the mechanics of the problem than ChatGPT did.1 Since Claude talked about the “moment diagram,” it’s worth showing the graph of this two-part function:

Moment diagram

Claude then correctly recognized expressed the relationship between the moment and deflection, y:

EId2ydx2=−M(x)

Note the negative sign, which ChatGPT never got right.

Claude plugs in its expressions for M(x) and integrates twice to get

EIy1=PLx24−Px36+C1x+C2

for the left half and

EIy2=C3x+C4

for the right half. I find it a little weird that it’s keeping the EI term attached to y instead of moving it to the other side of the equations, but it’s OK to do it this way.

And Claude is also correct in how to solve for the four constants of integration. The deflection and slope at the fixed end are zero, and the deflection and slope at the center must match. As equations (which Claude doesn’t show), these conditions are

y1(0)=0andy1′(0)=0

at the fixed end and

y1(L2)=y2(L2)andy1′(L2)=y2′(L2)

at the center, where I’m using prime notation to represent derivatives.2

Claude doesn’t show the algebra that solves these four equations in four unknowns, nor does it give the values for C1, C2, C3, and C4. Which is a shame, because somehow, after doing everything else right, it screws up a simple algebra problem.

Aside
You may think “four equations in four unknowns” isn’t especially simple, but you can solve them in a particular order to avoid simultaneous equations. Like this:

Start with

y1(0)=0⇒C2=0

Similarly,

y1′(0)=0⇒C1=0

Using these values, we move onto

y1′(L2)=y2′(L2)⇒C3=PL28

and finally

y1(L2)=y2(L2)⇒C4=−PL348

These values will give the correct equations for the deflection.

Instead of showing its work, Claude skips to the “solution,” which it gives as

δ=11PL348EI

This is not only wrong, its the same wrong answer that ChatGPT gave, albeit for different reasons, which I find quite strange.

In summary:

Leon offered to ask Claude to explain itself further, but I think this is enough. Maybe I’ll return to this problem in another couple of years.

  1. ChatGPT did get the bending moments correct in its last explanation, but its initial moments were wrong. ↩

  2. If you’re reading this in Safari or Chrome, the primes are a little anemic, and you might think they’re just specks of dust on your screen. Also, they’re higher than they ought to be. Firefox does a better job, both in the readability and placement of the primes. ↩

Next post Previous post