Other wavy paths
October 28, 2025 at 12:25 PM by Dr. Drang
I got some good replies on Mastodon after Saturday’s post. Longtime friend of the blog Nathan Grigg said he’s always assumed that GPS-measured lengths would be long because no matter how straight your path, the GPS error would make it zigzagged. Then wherami and thvedt pointed out that the official rules of these events say that the race’s distance is supposed to be measured along the shortest path. If the road is curving left, it should be measured along the left edge; if the road is curving right, it should be measured along the right edge. This makes sense, as you don’t want runners to be able to run less than the official distance.
As you can see from this Fitness app screenshot of my route, the 5k at the Morton Arboretum has both right and left curves, so the route measurement must be done carefully if it’s to be by the rules.
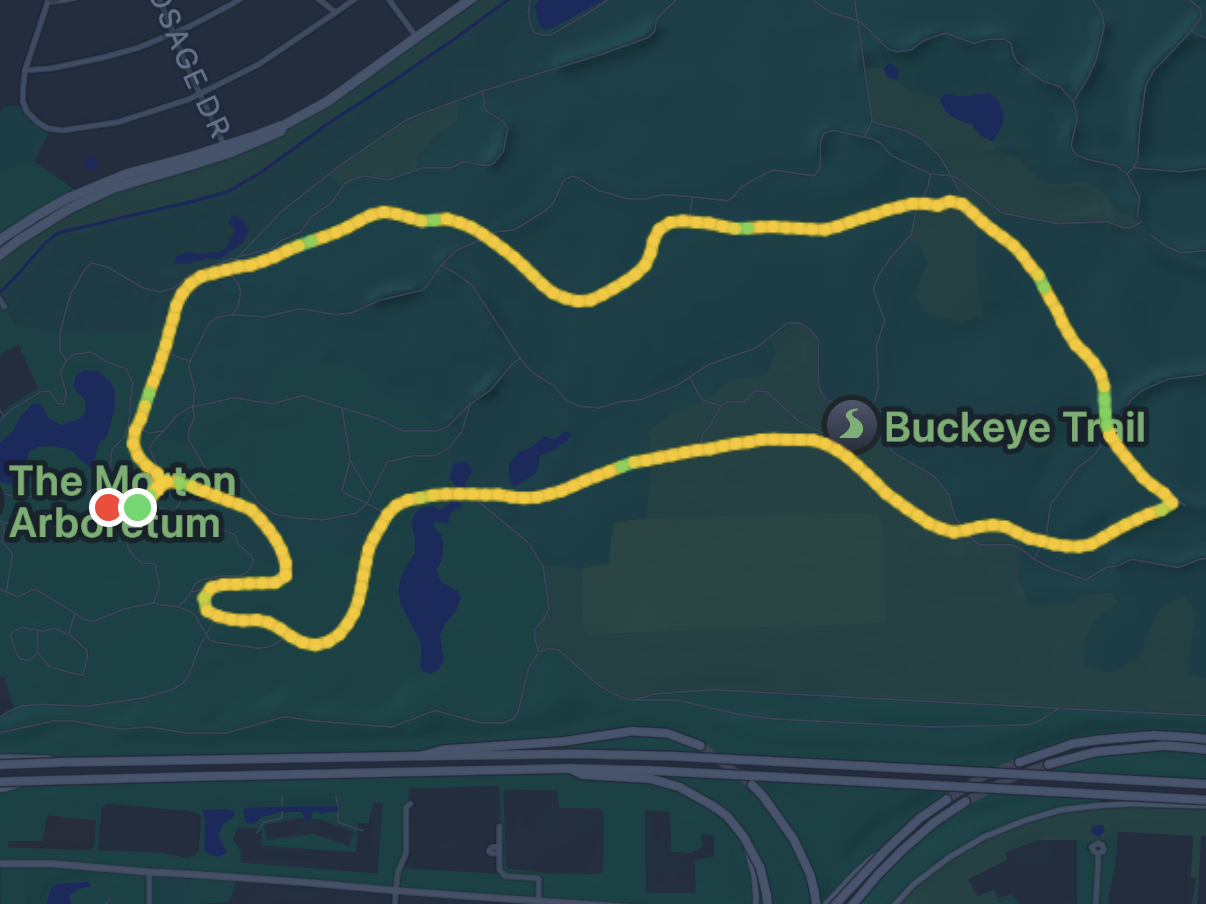
I began thinking about calculating the length of a zigzag path along a road that went in a circuit. The simplest circuit is a circle, and I thought it would be easier to define my path as a sinusoid within the roadway. Like this:
Following the principle that you should walk before you run, I started with a simpler problem: a sinusoidal path along a straight road.
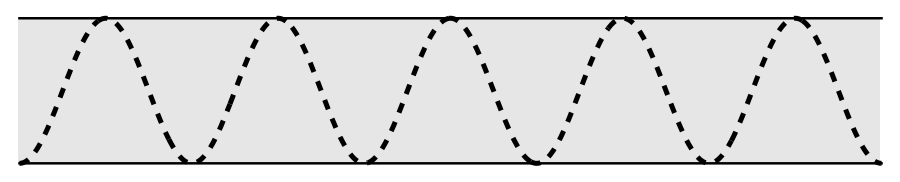
Taking the length of the road as and the width as , I defined the wavy path as
where the axis runs along the bottom edge of the road, and the axis runs across the road.
A differential length of arc is
Integrating this from to gives us the length of the wavy path. This can be done through elliptic integrals, but I’ve never felt comfortable with them, so I just did it numerically, using , , and plugging in different values of until I got a result of , which is, as you might recall, the distance my watch gave as I finished the race.
The answer I got was . Here’s the Mathematica code that got me there:
This is slightly less than the I got in Saturday’s analysis, where I took the path to be a series of straight-line segments. The lower number for a sinusoid makes sense. The path distance from one edge of the road to another is longer when following a sinusoid than when going in a straight line.
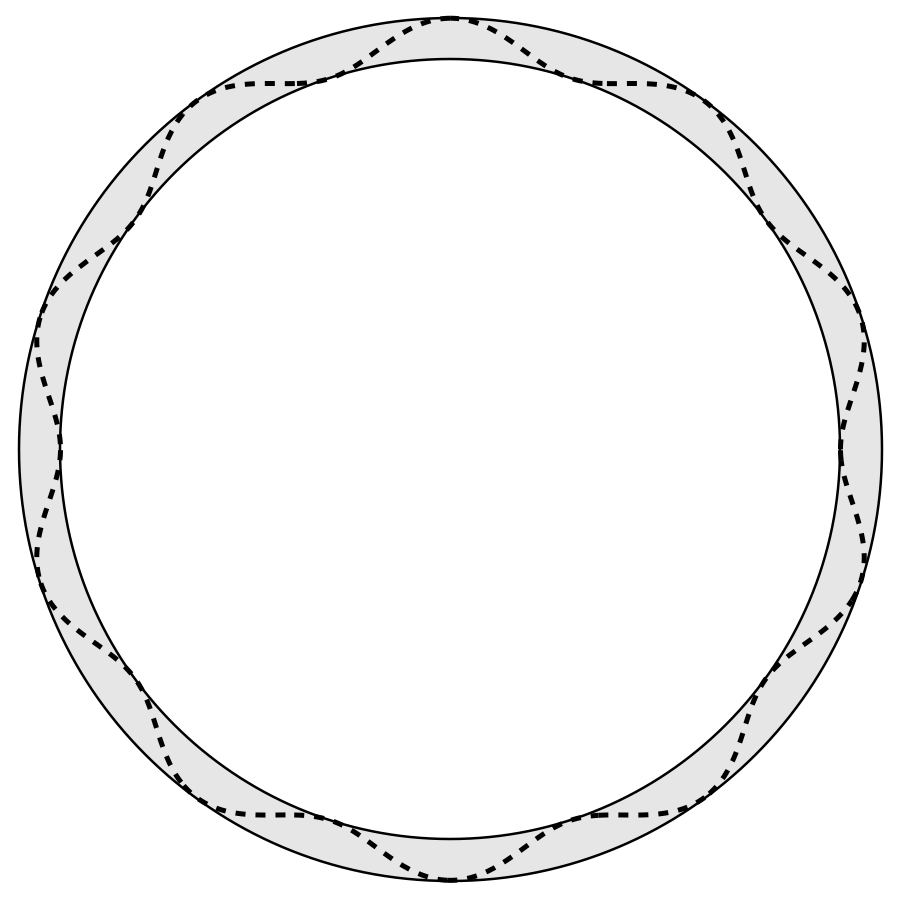
Now let’s tackle the problem of a wavy path along a circular road. Polar coordinates seem like our best bet for this. We’ll define the radius of the wavy path as
where
is the radius of the inside edge of the circle, the circumference of which is the 5000 m length of the race. We’ll use as before.
In polar coordinates, differential arc length has a more complicated definition:
Numerical integration of this over from to with different values of led to a solution of to get a path length of . Here’s a screenshot of the Mathematica code:
I used t for because it’s easier to type.
That this value of is smaller than for the straight road makes sense because all of the path is beyond the inner edge of the roadway. The waviness is centered on a path that’s already longer than the course.
I suppose I could have set up iterative solutions in Mathematica to get the values of n that led to path lengths of 5070. But NIntegrate worked so quickly that it was faster to just work my way to n via trial-and-error.
I should also mention that Mathematica has an ArcLength function, which seemed at first like the right way to go. But it was extremely slow, possibly because it was trying to get an analytical solution. By doing a little thinking to get the equations for the differential arc length, I saved myself a lot of time.