And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Previous post

Zigzag 5k

October 25, 2025 at 2:43 PM by Dr. Drang

I did the Fall Color 5k Run and Walk at the Morton Arboretum this morning. I say “did” to downplay the fact that I don’t run races like this, I walk them. I got terrible shin splints 20+ years ago and haven’t run more than a few hundred meters at a time since then. But I do try to walk at a decent clip. My goal is to do these races in under 45 minutes, and I managed that this morning. Here’s a screenshot of my watch as I crossed the finish line.

The time of 43:38 matched my official time to the second, so I’m confident the start/stop I did on my watch was accurate. What’s off, though, is the distance. My watch says I went 70 meters more than 5k. How can that be?

The obvious answers are that either my watch is slightly off through an accumulation of small GPS errors or the course distance is slightly off because it wasn’t measured perfectly. Could also be some combination of both.

But these answers—although probably right—are dull and don’t let me try out any calculations. Because I started the race late (very long traffic backup at the entrance; also today was the first time I slept past 6:30 for as long as I can remember), I had to pass a lot of people on the route. Could it be that my zigzag path along the road through the Arboretum added 70 meters to my walk?

Let’s simplify the problem to make it tractable. Imagine a straight road 5 m wide and 5000 m long. I take a zigzag path down the road, with each zig and zag of the same length and the full width of the road. How many of these zigzags are needed to end up with a path length of 5070 m, and is that answer reasonable?

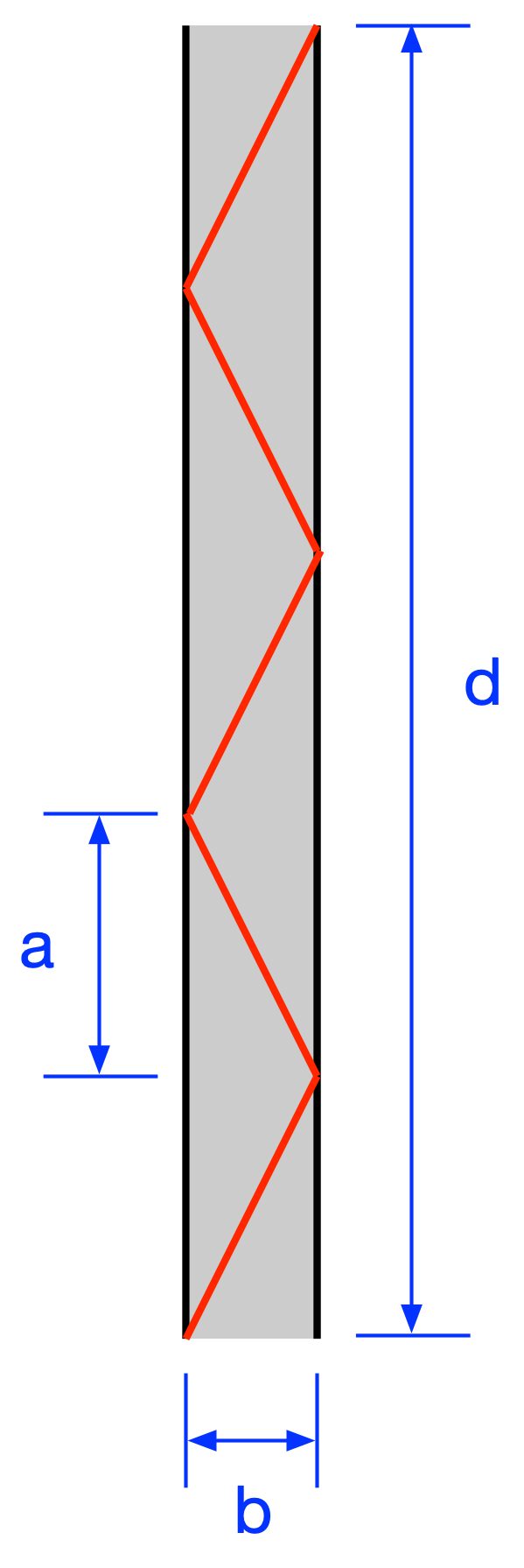
We’ll take $n$ as the number of zigs and zags, so

$$d=na$$

The total length of my walk is

$$\ell =n\sqrt{a^2+b^2}=n\sqrt{\frac{d^2}{n^2}+b^2}=\sqrt{d^2+n^2{b}^2}$$

With $d=5000\mathrm{m}$, $b=5\mathrm{m}$, and $\ell =5070\mathrm{m}$, what is $n$?

Since

$${\ell }^2=d^2+n^2{b}^2$$

we can solve for $n$:

$$n=\sqrt{\frac{{\ell }^2-d^2}{b^2}}$$

Now, when you’re taking the difference of two numbers that are relatively close to one another, you’re supposed to be careful about losing significant digits. Here, $\ell$ and $d$ differ by enough that we really don’t have to worry about that, but let’s be good boys and girls anyway.

Rewrite $\ell$ as

$$\ell =d+ϵ$$

Then

$${\ell }^2=d^2+2dϵ+{ϵ}^2$$

and

$${\ell }^2-d^2=2dϵ+{ϵ}^2$$

so

$$n=\sqrt{\frac{2dϵ+{ϵ}^2}{b^2}}$$

and we won’t lose any significant digits because we’re adding, not subtracting.

Plugging in the numbers, we get

$$n=\sqrt{\frac{2\cdot 5000\cdot 70+{70}^2}{5^2}}=167.9$$

Is it reasonable to think I zigged and zagged 168 times? No. That’s one full crossing of the road every 30 meters or so, which is ridiculous.

So we’re left with the duller but more reasonable answer that my 5.07 km distance is some combination of measurement errors. Disappointing.

Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2025, Dr. Drang