Equation of time
December 9, 2025 at 9:01 PM by Dr. Drang
Speaking of the equation of time, which I was in yesterday’s post, I wanted to extend some of the work I did in that post to draw my own EoT plot and to be able to adjust it to show the difference between solar time and standard time anywhere on Earth.
In Mathematica, solar time is best tackled with the SunPosition function.1 This function can be called in a variety of ways. We’ll focus initially on getting the Sun’s position at noon at a point on the Prime Meridian, and we want the position given as the right ascension and declination. These are equatorial coordinates on the celestial sphere. Because we’re doing time calculations, only the right ascension—which is the longitudinal coordinate—matters to us. Luckily, right ascension is given not in degrees, but in time units: hours, minutes, and seconds. This is a useful unit in astronomy because the difference in right ascension between two celestial objects is the time gap between their passage over the observer’s local meridian. You can find a good explanation of celestial coordinates at Sky & Telescope.
For standard time, we have to be a little careful. Since we’re measuring the Sun in terms of right ascension, we should do the same for standard time. That means getting the sidereal time of the location on Earth, which is the right ascension of the local meridian for a given time.
In simplest terms, we have two right ascensions, one for the Sun’s position and one for the sidereal time. We take their difference to get the equation of time. Unfortunately, there’s a practical complication that messes up this seemingly simple calculation. Right ascension is never greater than 24 hours—it wraps around back around to zero. So we can have right ascension values that are close to one another but don’t seem to be close at all. For example 23:57:00 and 00:2:30 are only 5½ minutes apart, but you get -23:54:30 if you subtract the first from the second. We have to manipulate the right ascension values before subtraction to make sure we get the correct difference.
The standard equation of time graph you’ll see on websites and in textbooks is plotted for a point on the Prime Meridian using UTC. Here’s what it looks like:
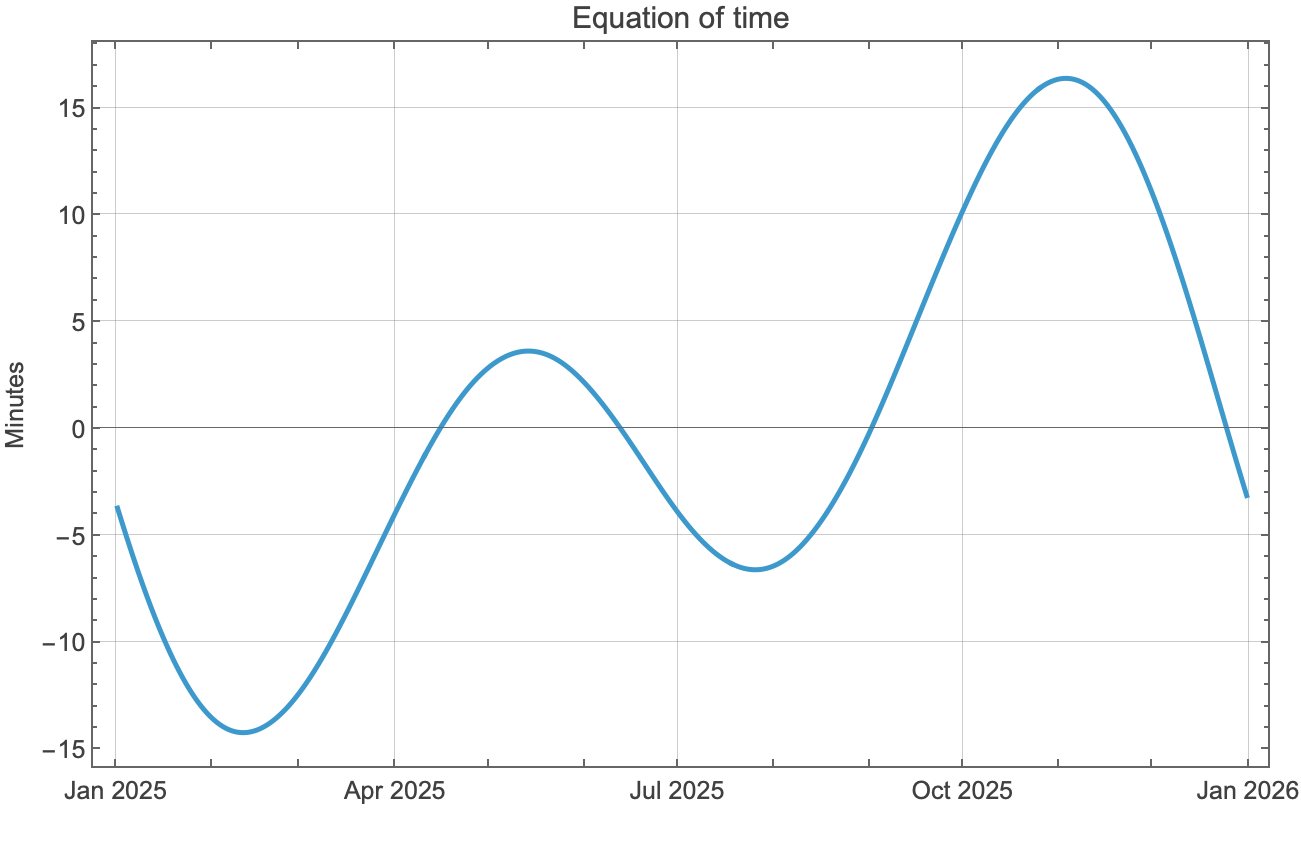
It’s plotted so that positive values represent periods for which the solar time is ahead of standard time, e.g. solar noon, when the Sun is at its highest point, comes before 12:00:00 UTC. Here’s the Mathematica notebook that produced the plot:
Some comments:
- The latitude of the point on the Prime Meridian doesn’t matter. I chose 51.5° because that’s about the latitude of the Royal Observatory in Greenwich.
- I chose local noon for the time at which to get the
SunPositionandSiderealTime. The pure function used in theMapcall to generate the list of Sun positions extracts only the first (right ascension) term of the position. - The initial plots of
sunposandstimeshow the wraparounds, or jumps, in right ascension as it exceeds 24 hours. The expressions forsunjumpandtimejumpreturn the lists, in reverse order, of the indices at which the jumps occur. The expressions are more complicated than they need to be for this particular problem because I wanted them to be able to handle longer date ranges in which there will be more than just one jump. - The two
Doloops—an expression I thought I’d given up when I stopped using Fortran—adjustsunposandstimeto get rid of the jumps. They, too, are built to handle longer date ranges with more jumps. The third graph showssunposandstimeafter the adjustments. - The difference between
sunposandstimecan now be calculated with a simple subtraction. The values are converted from hours to minutes because that’s a more convenient unit. The subtraction is done asstime - sunposbecause that means we’ll get positive numbers when the Sun is ahead (west) of the Prime Meridian and negative numbers when the Sun is behind (east) of the Prime Meridian.
You may recall from yesterday’s post that I said solar noon was currently about 15 minutes ahead of standard noon in Naperville, Illinois, where I live. That doesn’t match up with the equation of time because Naperville isn’t on the Prime Meridian, nor is it on the 90° W meridian, which would match up perfectly with the local UTC-6 timezone. I wanted to make an adjusted equation of time plot to account for that. Also, I wanted winter to be at the center of the graph, not split between the left and right edges.
Here’s the adjusted graph:
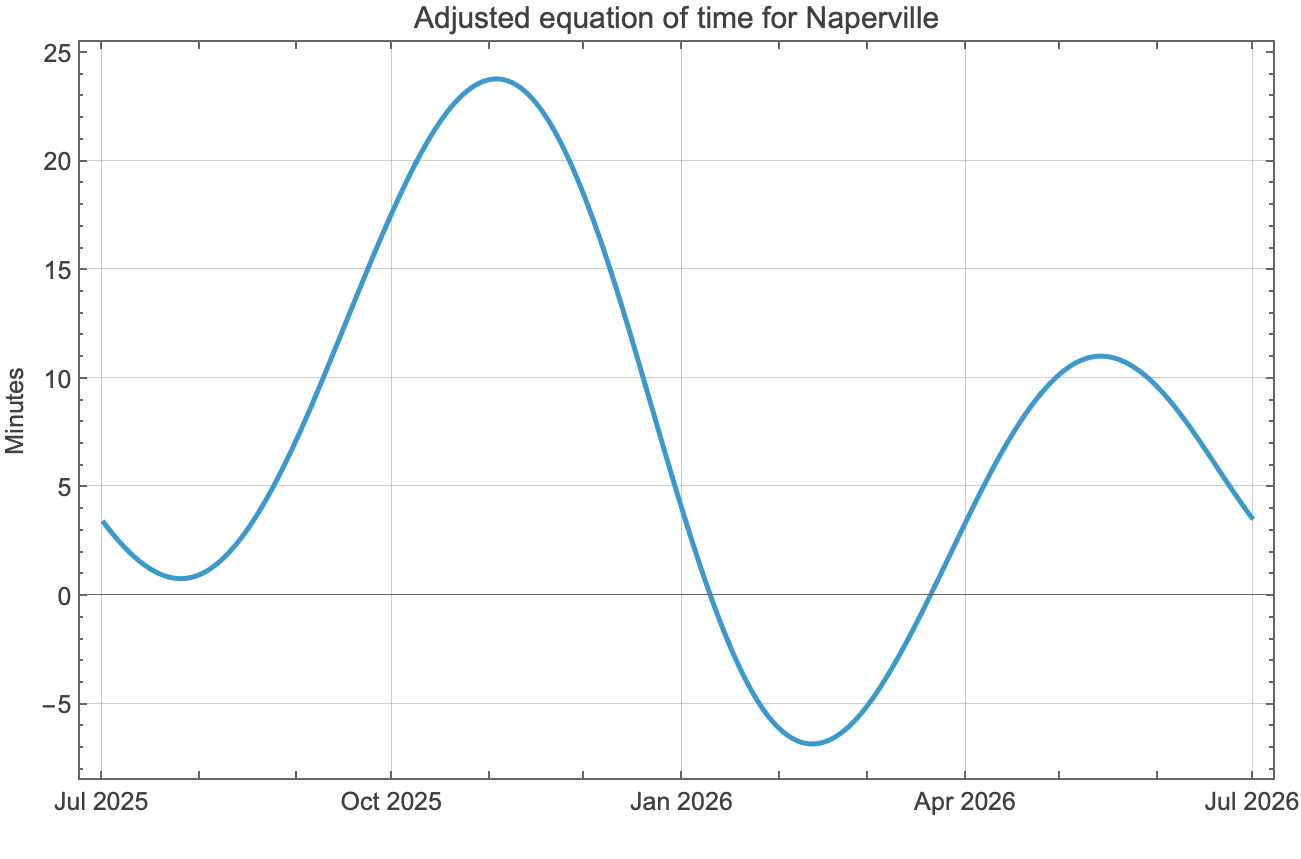
Apart from the six-month sideways shift, the graph is pushed up because Naperville is about 1.85° east of the 90° W meridian. With a four-minute difference for every degree, that means the whole graph is about minutes higher than standard equation of time.
Here’s the notebook that made the graph:
The changes are all at the top of the notebook: different coordinates for the location, different start and end dates, and a different timezone. But the rest of the notebook is the same as before.
-
In the Applications section of the
SolarPositiondocumentation, there’s an example calculation and graph of the equation of time, but I don’t like it. The calculations it goes through are both hard to follow and can’t be applied to locations off the Prime Meridian. ↩
