Solving a snaky math problem with Mathematica
December 6, 2025 at 10:58 AM by Dr. Drang
I’m in the middle of a three-lecture series on the Wolfram Language and thought the puzzle presented in this recent MindYourDecisions video would be a good problem to practice on. Here’s the problem:
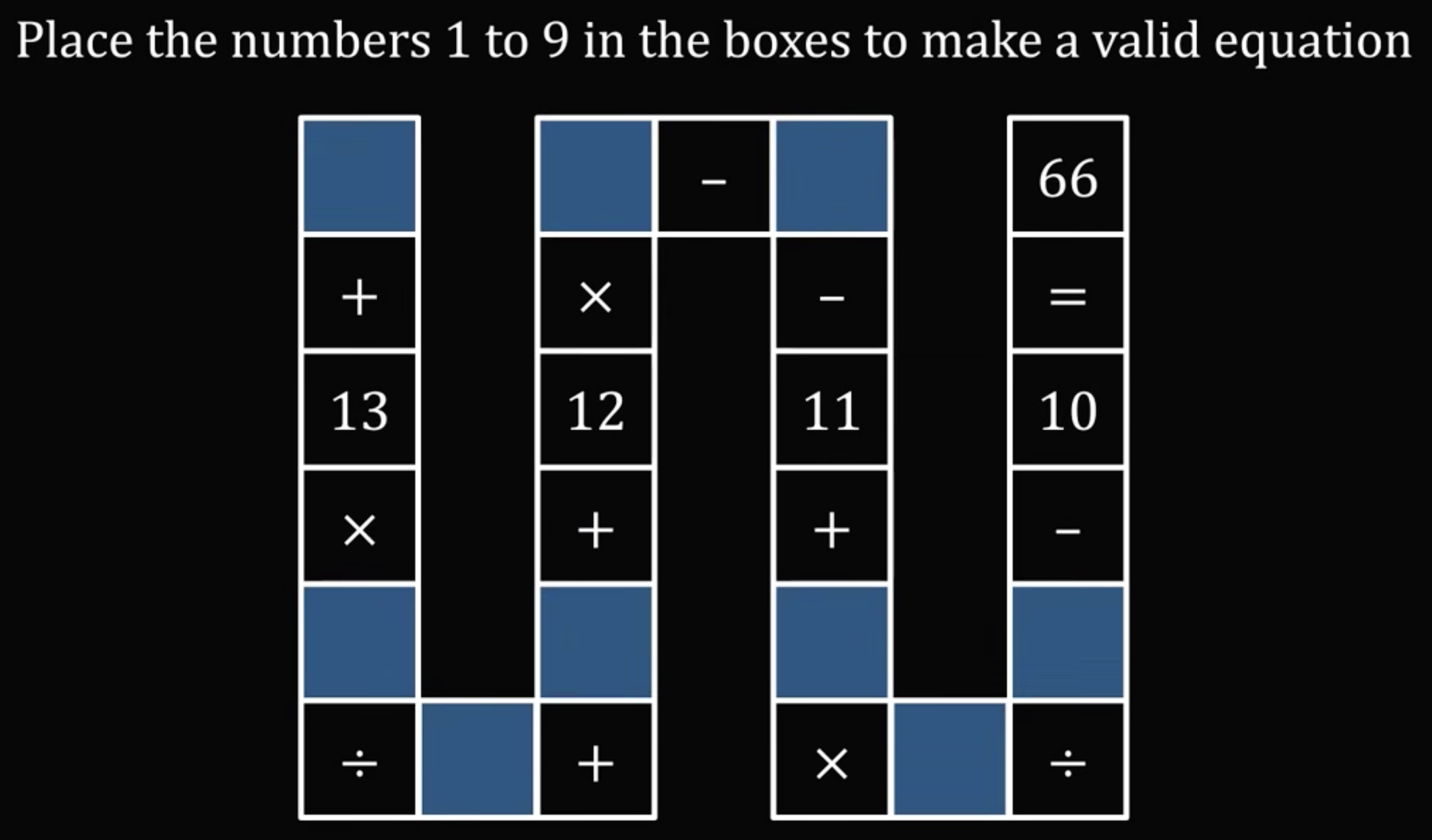
I’ll call the variables represented by the blue boxes through , and rewrite the equation in a more standard form:
I’m using for the variable names to emphasize that these are integers.
In the video, Presh Talwalkar shows some solutions by trial and error and then goes on to write a Python script that generates all the solutions via the itertools and fractions libraries. He uses fractions to avoid the problem of inexact floating point numbers appearing in the divisions of the second and seventh terms of the equation. Mathematica maintains the exact rational values when you divide integers, so I didn’t have to worry about that. Here’s the notebook with my work:
It starts by generating a list of the numbers 1 through 9 with the Range function and then generates the 362,880 permutations of that list via Permutations. The semicolon after the Permutations call keeps Mathematica from printing out all the permutations. There’s then a quick check to make sure the Length of the perms list is .
Filtering perms to get just the solutions to the equation is done with the Select function. I first define a function, f, that takes a list of values as its argument and returns true or false, depending on whether that list solves the equation. perms and f are then passed to Select to get all the permutations that solve the equation. There are 136 of these.
Because addition and multiplication are commutative, Talwalkar considers any switch of and or and to be essentially the same solution. Eliminating these switches leaves “base” solutions. I pull these from the list of all solutions by another use of Select, this time passing it a new function, g, that returns true only if and . That gives me these 34 base solutions:
1 2 6 4 7 8 3 5 9 1 3 2 4 5 8 7 9 6 1 3 2 9 5 6 4 7 8
1 3 4 7 6 5 2 9 8 1 3 6 2 7 9 4 5 8 1 3 9 4 7 8 2 5 6
1 4 8 2 7 9 3 5 6 1 5 2 3 4 8 7 9 6 1 5 2 8 4 7 3 9 6
1 5 3 9 4 2 7 8 6 1 8 3 7 4 5 2 6 9 1 9 6 4 5 8 3 7 2
1 9 6 7 5 2 3 4 8 2 1 4 3 7 9 5 6 8 2 6 9 8 5 1 4 7 3
2 8 6 9 4 1 5 7 3 2 9 6 3 5 1 4 7 8 3 2 1 5 4 7 8 9 6
3 2 4 8 5 1 7 9 6 3 2 8 6 5 1 7 9 4 3 6 4 9 5 8 1 7 2
3 9 2 8 1 5 6 7 4 5 1 2 9 6 7 3 4 8 5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6 5 4 8 9 6 7 1 3 2 5 7 2 8 3 9 1 6 4
5 9 3 6 2 1 7 8 4 6 3 1 9 2 5 7 8 4 7 1 4 9 6 5 2 3 8
7 2 8 9 6 5 1 3 4 7 3 2 8 5 9 1 6 4 7 5 2 8 4 9 1 3 6
7 6 4 8 5 9 1 3 2
This is basically where the video ends. But I noticed that many of the solutions give fractions for the second and seventh terms, and it just works out that the sum of those fractions is an integer. For example, plugging the values of the first solution into the equation gives:
This is true in part because
Most of the other solutions follow this pattern, where the second and seventh terms are fractions that sum to an integer. I wondered if there were any solutions for which the second and seventh terms were themselves integers.
So I wrote a new function, h, which returns true only if both of those divisions return integer values. I used Select with this function and the solns list to learn that 20 of the 136 solutions meet this criterion. I then applied g to this list to return just the five “base” versions, for which and :
3 2 1 5 4 7 8 9 6
5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6
5 9 3 6 2 1 7 8 4
6 3 1 9 2 5 7 8 4
I could have simply used Select to filter basesolns by h and gotten the same answer.
In the class, I’m learning to use anonymous functions to make the code faster and simpler. In this problem, speed is not an issue, and I think the code would be harder to follow if I used anonymous functions. Maybe I could replace g and h with anonymous functions with no loss of clarity, but I really think f should remain as-is.
