Latest sunrise and earliest sunset
December 8, 2025 at 6:09 PM by Dr. Drang
Here’s a fun post by Andrew Plotkin. He’s a late riser, so the shortest day of the year, which is on the solstice, means nothing to him. He’s interested in the date of the earliest sunset, because that means his sunlight hours will be increasing after that date. He calls it the Nighthawk’s Solstice and figures that it’s today, December 8.
But there’s some ambiguity:
It’s a bit tricky to pin down which day this is. There’s a million ad-encrusted sites which show you sunset times, but they mostly work in minutes, which means there’s a stretch of days which are “the earliest”. It’s the bottom of a long flat curve.
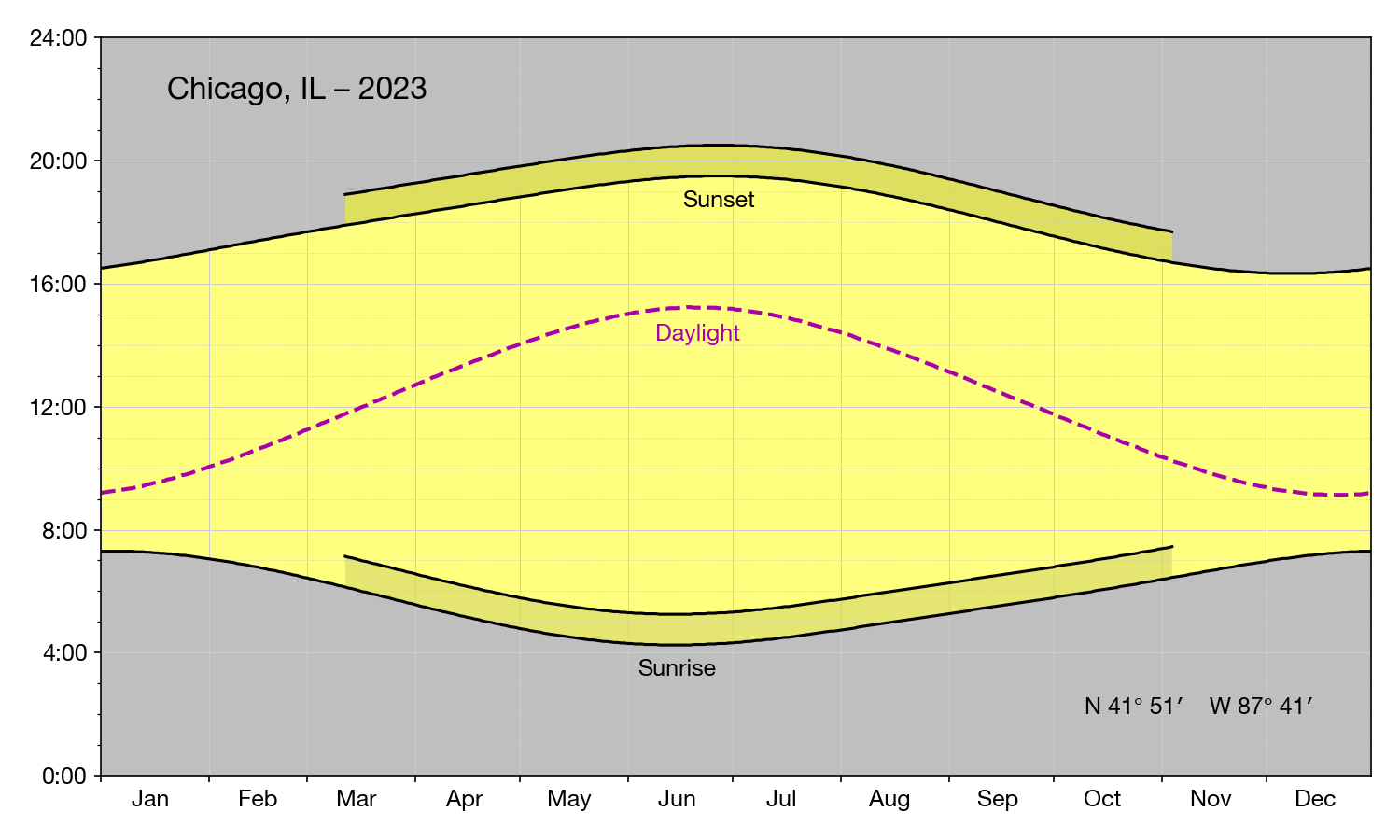
He could avoid the ads by going to this US Naval Observatory website. But that won’t solve the long flat curve problem. He’s run into the same problem I did a couple of years ago when I was trying to position the “Sunrise” and “Sunset” labels on my sunlight plots.
As I said back then:
Because the USNO data reports the sunrises and sunsets to the nearest minute, the minimum value of sunrise and maximum value of sunset last for several days. I want the labels to be centered within those stretches.
What’s true for the earliest sunrise and latest sunset is also true for the latest sunrise and earliest sunset. My solution for positioning the labels was the same as Andrew’s solution for fixing the date of Nighthawk’s Solstice: picking the date in the middle of the flat stretch.
Since I’ve been using Mathematica a lot lately, I wondered if I could do better. And I can. Mathematica has Sunrise and Sunset functions that return the dates and times to the nearest second. So I made this short notebook to find the latest sunrise and earliest sunset for Naperville, Illinois, where I live:
It first sets the location for all the calculations to the Nichols Library in downtown Naperville and circles the location on a satellite view. It then uses the DateRange and DateObject functions to build a list of dates from the beginning of December to the middle of January.
Passing that list of dates to Sunrise and Sunset returns an EventSeries for each. The Values property for these series extracts just the time and date for each sunrise and sunset. Finally, using MaximalBy pulls out the sunrise with the latest time. Similarly, using MinimalBy for the sunsets gets the sunset with the earliest time.
As you can see, Andrew’s eyeball estimate of December 8 as the earliest sunset is correct.1 So today is (or was—I’m typing this after sunset) Nighthawk’s Solstice.
A few comments:
- If you look carefully at the documentation for
SunriseandSunset, you’ll see that they have lots of options for zeroing in on exactly what kind of sunrise or sunset you’re calculating. Are you looking for when the middle of the sun is at the horizon? The upper limb? The lower limb? And are you accounting for refraction? What about elevation? As you can see from the code, I’m accepting Mathematica’s defaults for all of those options. I’m not especially worried about any imprecision that might creep in because of this. I don’t care about the exact rise and set times, only in how they change from day to day. As long as I’m consistent in the method of calculation, the dates of the minimum and maximum should be correct. - Since I’ve brought up refraction, you might well argue that Mathematica’s calculations of sunrise and sunset to the nearest second is bullshit. The refractive index of air changes with the weather, so you’ll never know sunrise or sunset with that kind of precision. I would just say that
SunriseandSunsetuse consistent assumptions that allow the calculations to proceed, real world observations notwithstanding. - If you’re wondering why the latest sunrise and earliest sunset don’t match up with the winter solstice, you should look into the equation of time. Today, solar noon here in Naperville was about 15 minutes before the noon on our watches.2 Sunrise and sunset are about equally spaced on either side of solar noon, so that means sunrise was about 4 hours and 53 minutes before watch noon and sunset was about 4 hours and 22 minutes after watch noon. It is that difference between solar and watch time that makes the earliest sunset happen before the solstice and the latest sunrise happen after.
Solving a snaky math problem with Mathematica
December 6, 2025 at 10:58 AM by Dr. Drang
I’m in the middle of a three-lecture series on the Wolfram Language and thought the puzzle presented in this recent MindYourDecisions video would be a good problem to practice on. Here’s the problem:
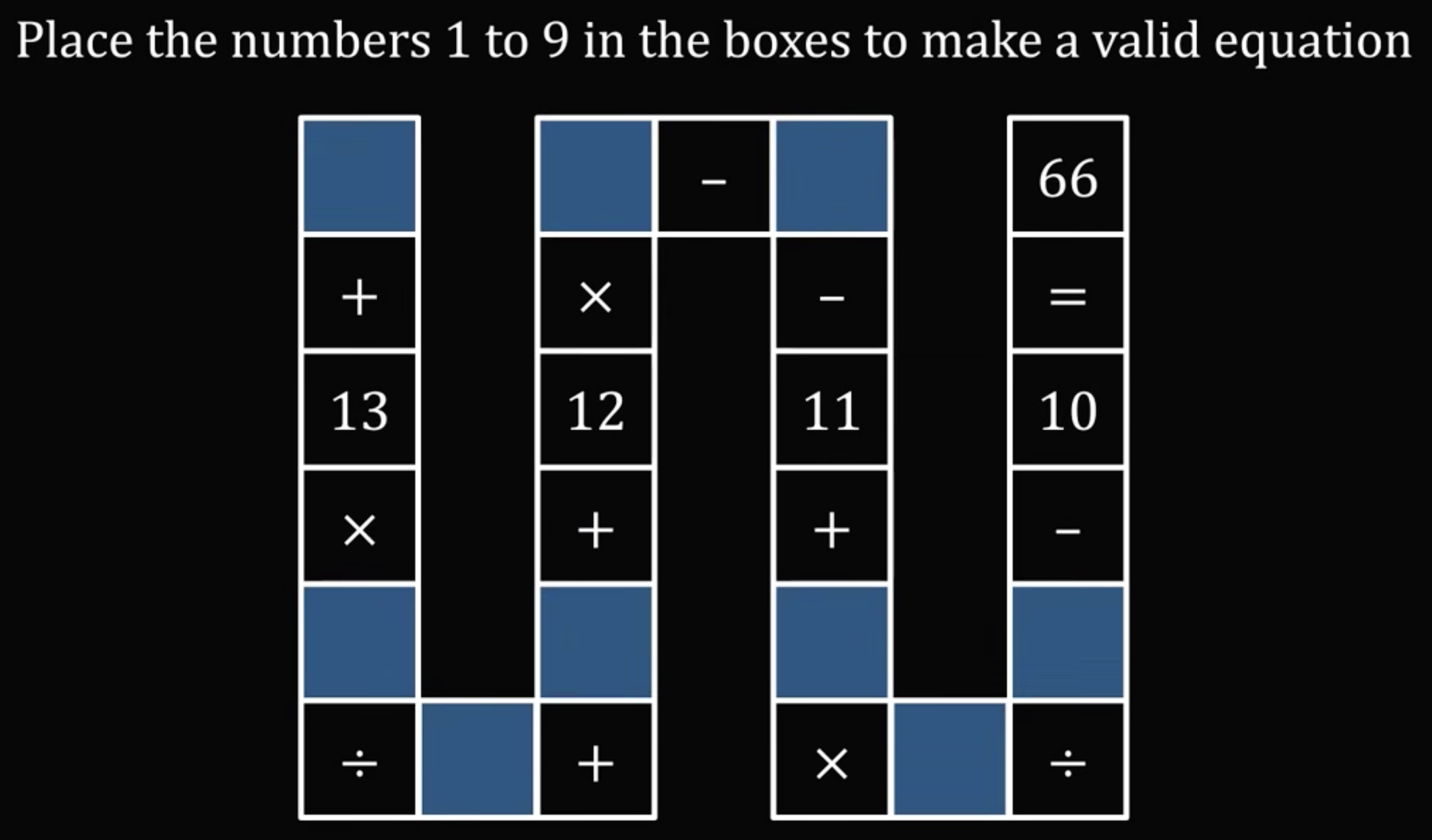
I’ll call the variables represented by the blue boxes through , and rewrite the equation in a more standard form:
I’m using for the variable names to emphasize that these are integers.
In the video, Presh Talwalkar shows some solutions by trial and error and then goes on to write a Python script that generates all the solutions via the itertools and fractions libraries. He uses fractions to avoid the problem of inexact floating point numbers appearing in the divisions of the second and seventh terms of the equation. Mathematica maintains the exact rational values when you divide integers, so I didn’t have to worry about that. Here’s the notebook with my work:
It starts by generating a list of the numbers 1 through 9 with the Range function and then generates the 362,880 permutations of that list via Permutations. The semicolon after the Permutations call keeps Mathematica from printing out all the permutations. There’s then a quick check to make sure the Length of the perms list is .
Filtering perms to get just the solutions to the equation is done with the Select function. I first define a function, f, that takes a list of values as its argument and returns true or false, depending on whether that list solves the equation. perms and f are then passed to Select to get all the permutations that solve the equation. There are 136 of these.
Because addition and multiplication are commutative, Talwalkar considers any switch of and or and to be essentially the same solution. Eliminating these switches leaves “base” solutions. I pull these from the list of all solutions by another use of Select, this time passing it a new function, g, that returns true only if and . That gives me these 34 base solutions:
1 2 6 4 7 8 3 5 9 1 3 2 4 5 8 7 9 6 1 3 2 9 5 6 4 7 8
1 3 4 7 6 5 2 9 8 1 3 6 2 7 9 4 5 8 1 3 9 4 7 8 2 5 6
1 4 8 2 7 9 3 5 6 1 5 2 3 4 8 7 9 6 1 5 2 8 4 7 3 9 6
1 5 3 9 4 2 7 8 6 1 8 3 7 4 5 2 6 9 1 9 6 4 5 8 3 7 2
1 9 6 7 5 2 3 4 8 2 1 4 3 7 9 5 6 8 2 6 9 8 5 1 4 7 3
2 8 6 9 4 1 5 7 3 2 9 6 3 5 1 4 7 8 3 2 1 5 4 7 8 9 6
3 2 4 8 5 1 7 9 6 3 2 8 6 5 1 7 9 4 3 6 4 9 5 8 1 7 2
3 9 2 8 1 5 6 7 4 5 1 2 9 6 7 3 4 8 5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6 5 4 8 9 6 7 1 3 2 5 7 2 8 3 9 1 6 4
5 9 3 6 2 1 7 8 4 6 3 1 9 2 5 7 8 4 7 1 4 9 6 5 2 3 8
7 2 8 9 6 5 1 3 4 7 3 2 8 5 9 1 6 4 7 5 2 8 4 9 1 3 6
7 6 4 8 5 9 1 3 2
This is basically where the video ends. But I noticed that many of the solutions give fractions for the second and seventh terms, and it just works out that the sum of those fractions is an integer. For example, plugging the values of the first solution into the equation gives:
This is true in part because
Most of the other solutions follow this pattern, where the second and seventh terms are fractions that sum to an integer. I wondered if there were any solutions for which the second and seventh terms were themselves integers.
So I wrote a new function, h, which returns true only if both of those divisions return integer values. I used Select with this function and the solns list to learn that 20 of the 136 solutions meet this criterion. I then applied g to this list to return just the five “base” versions, for which and :
3 2 1 5 4 7 8 9 6
5 3 1 7 2 6 8 9 4
5 4 1 9 2 7 3 8 6
5 9 3 6 2 1 7 8 4
6 3 1 9 2 5 7 8 4
I could have simply used Select to filter basesolns by h and gotten the same answer.
In the class, I’m learning to use anonymous functions to make the code faster and simpler. In this problem, speed is not an issue, and I think the code would be harder to follow if I used anonymous functions. Maybe I could replace g and h with anonymous functions with no loss of clarity, but I really think f should remain as-is.
Date calculations on the iPhone
December 5, 2025 at 6:19 PM by Dr. Drang
Back in early 2023, I wrote about combining some of my simple command-line date commands into a single Keyboard Maestro macro. This became my go-to system for quickly getting the number of days between two dates. Around that same time, I wrote a shortcut so I could make the same quick calculation on my iPhone (or iPad, but I don’t think I’ve ever used it there). For some reason, I never wrote about the shortcut here, even though I’ve used it a lot.
The shortcut, called Days Between, displays a date picker for the start date,
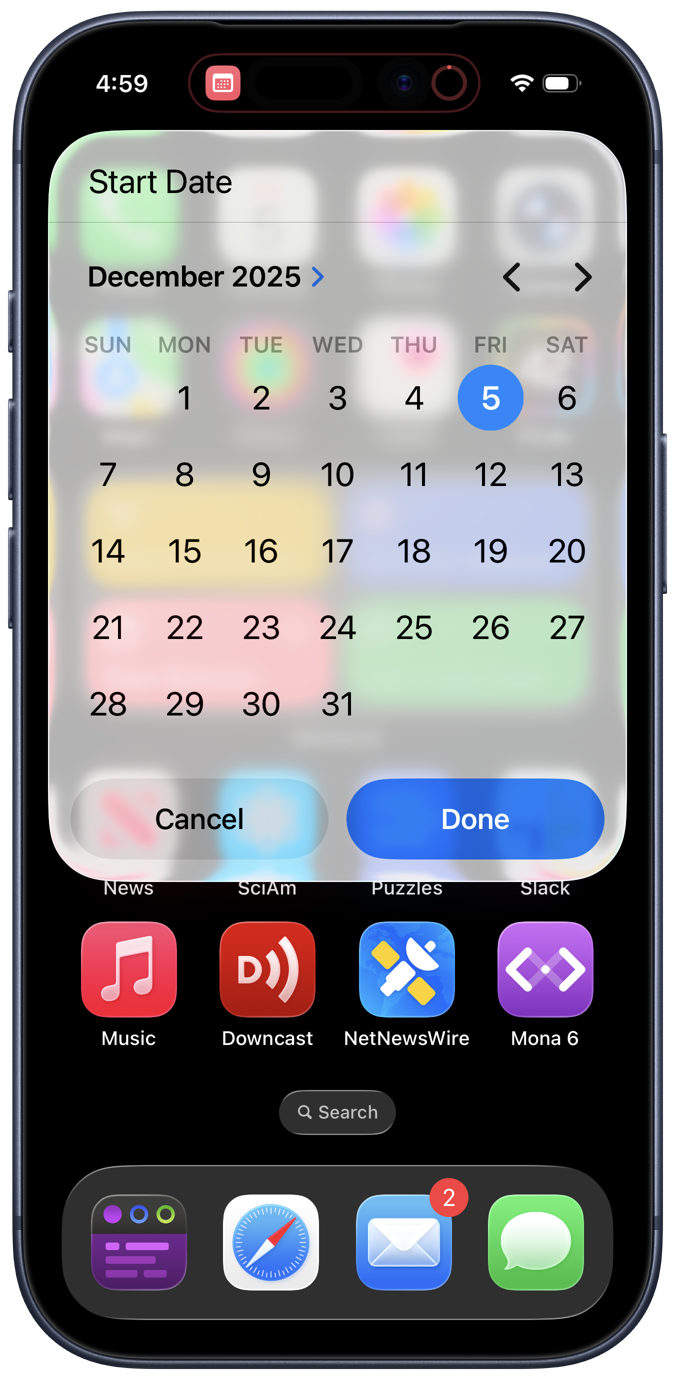
and the end date, which looks the same except for the text at the top. It then calculates the number of days between the two dates and displays the answer:
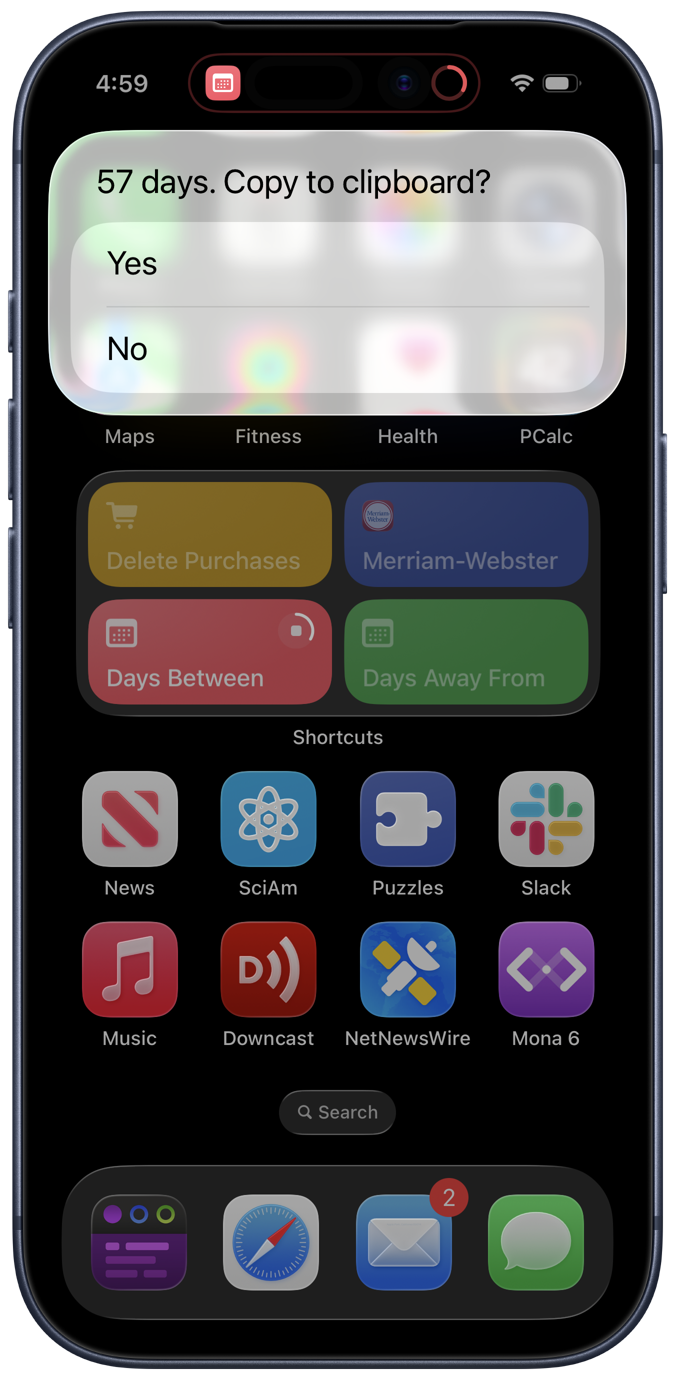
In this case the answer was between today and January 31 of next year.
The defaults for both the start and end dates are the current day because that’s likely to be what I want for one of them. Along with the answer, I’m given the opportunity to copy the result to the clipboard in case I want to paste it into a text or email.
Days Between is easy to use and was easy to write. Here are the steps:
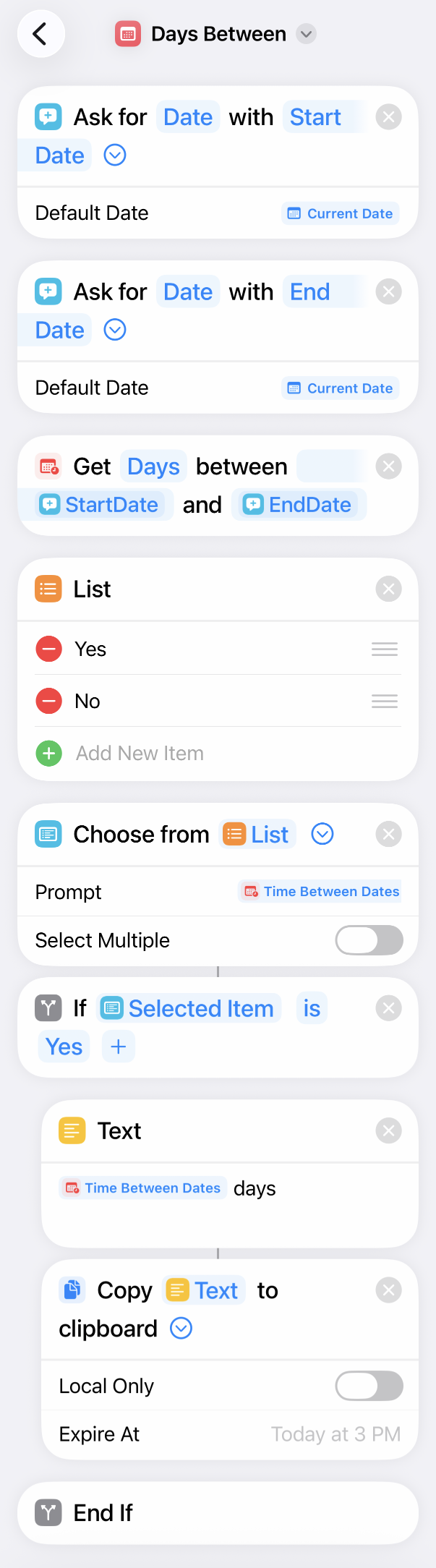
I don’t think the steps need to be explained. If you think you’d use Days Between, download it.
A similar shortcut, called Days Away From, asks for the start date and a number of days. Unsurprisingly, it returns the date that many days away from the start date. I’m sure you don’t need to see screenshots of it in action, but here are the steps:
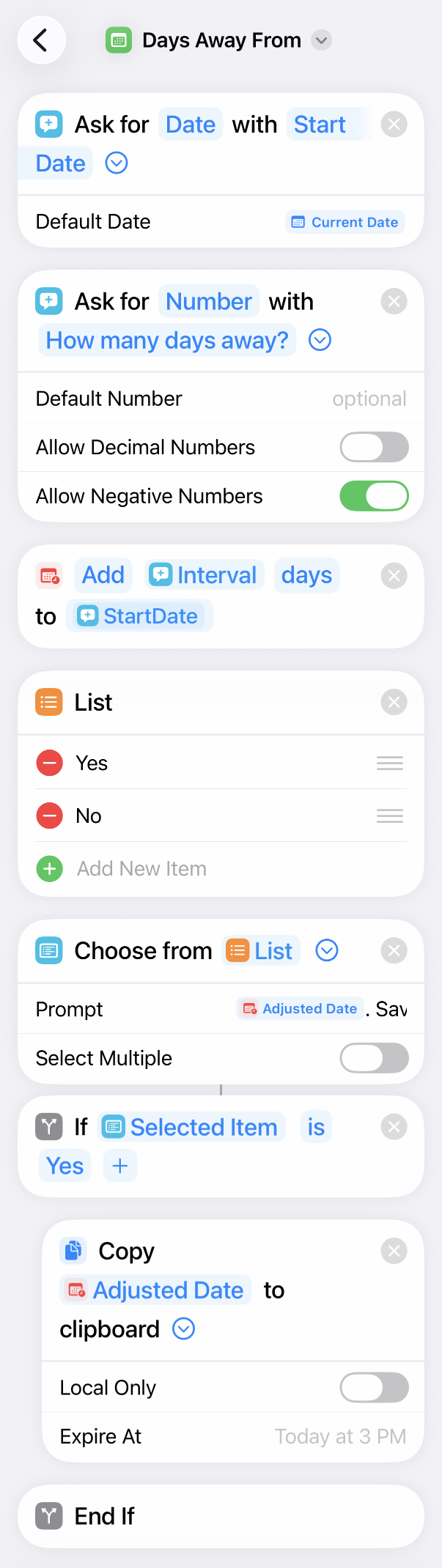
Again, you can download it if you think it would be helpful.
I’ve been running these shortcuts via buttons on a 2×2 Shortcuts widget on my home screen for quite a while, but I think I’ll be removing them soon. A few days ago, sharon linne faulk told me on Mastodon about a $3 app called Time Jump that does what both of my shortcuts do but with a simpler UI.
Here’s what Time Jump looks like upon launch:
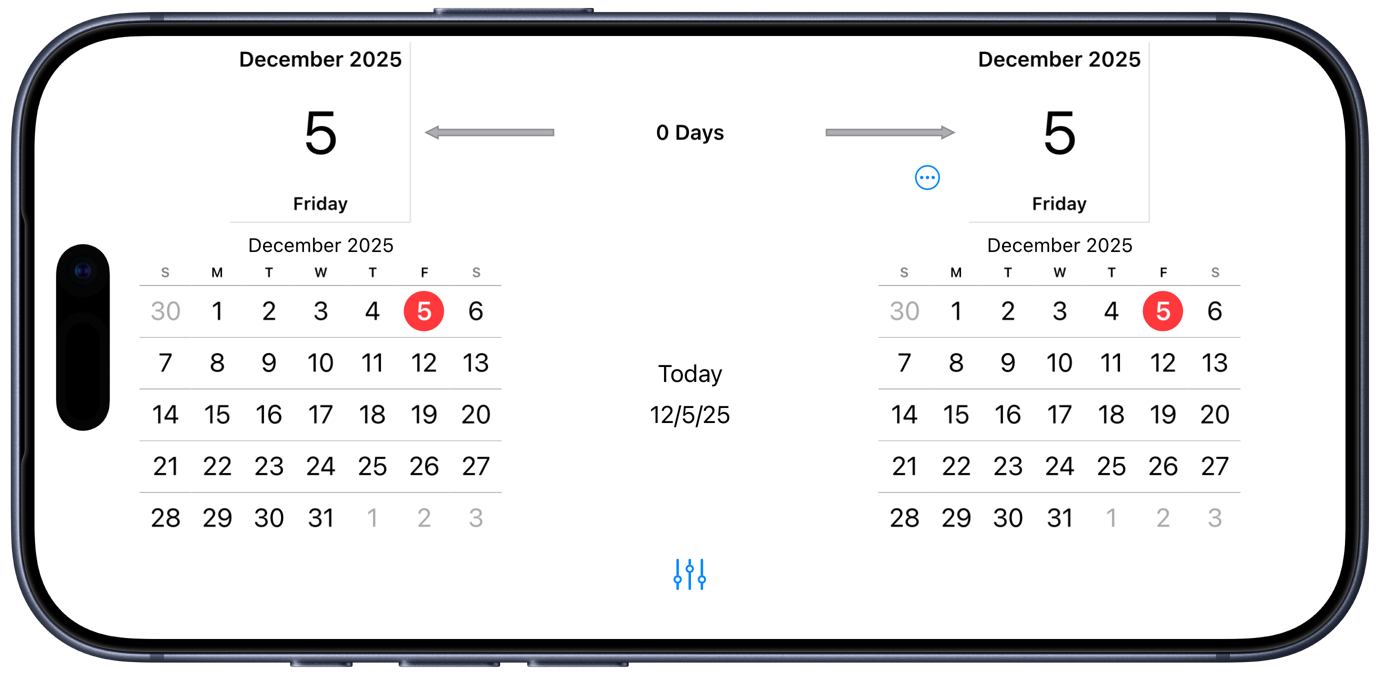
By working only in landscape mode, it can show two date pickers side by side with the interval information in between. Initially, both dates are set to the current date. Swipe and tap to change the dates and the display updates automatically to show the interval:
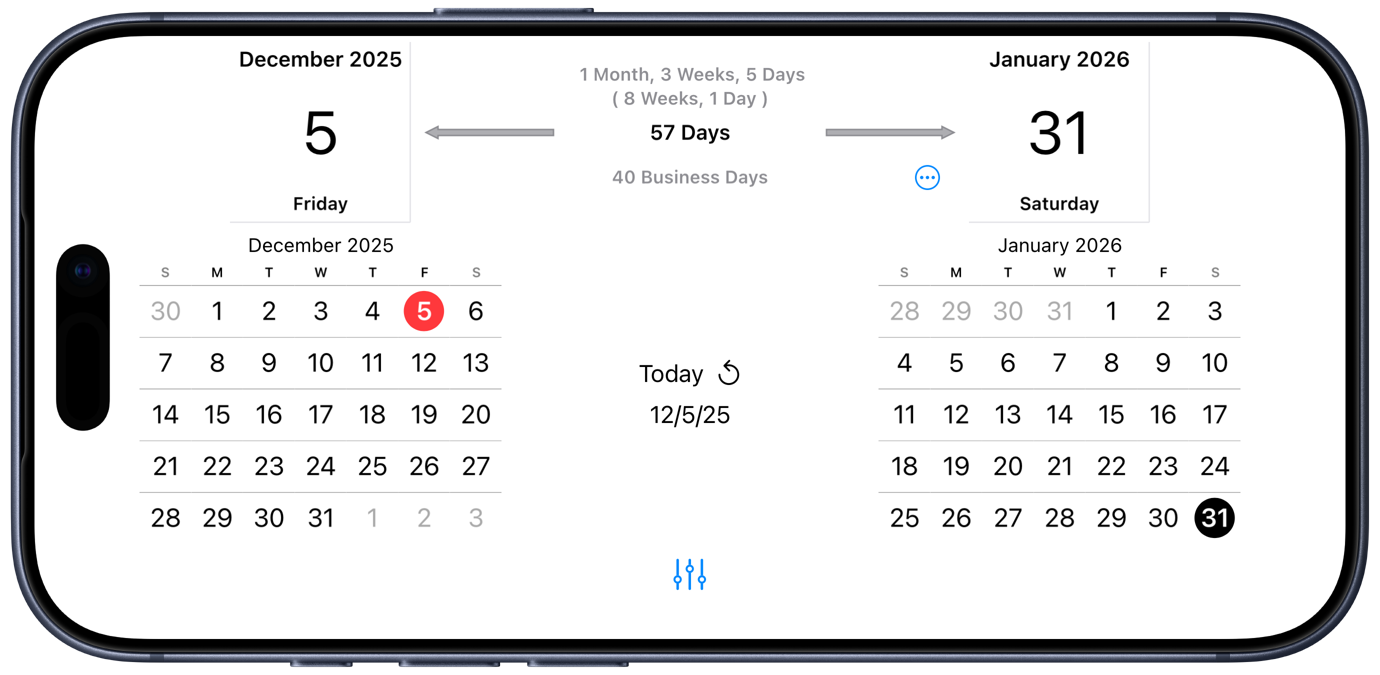
Tap on the three-dot button to pop up a number pad in which you can enter the day interval:
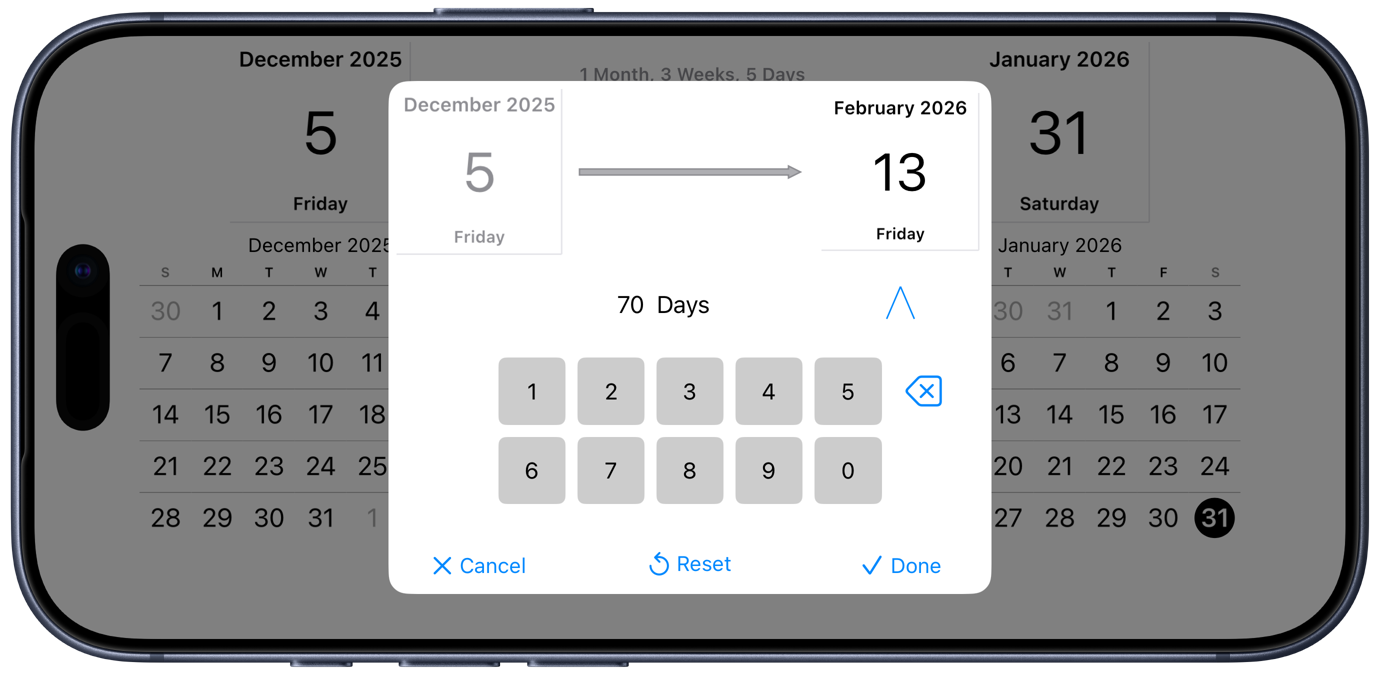
The end date updates as you type in the number of days, and that date persists on the main screen when you dismiss the keyboard:
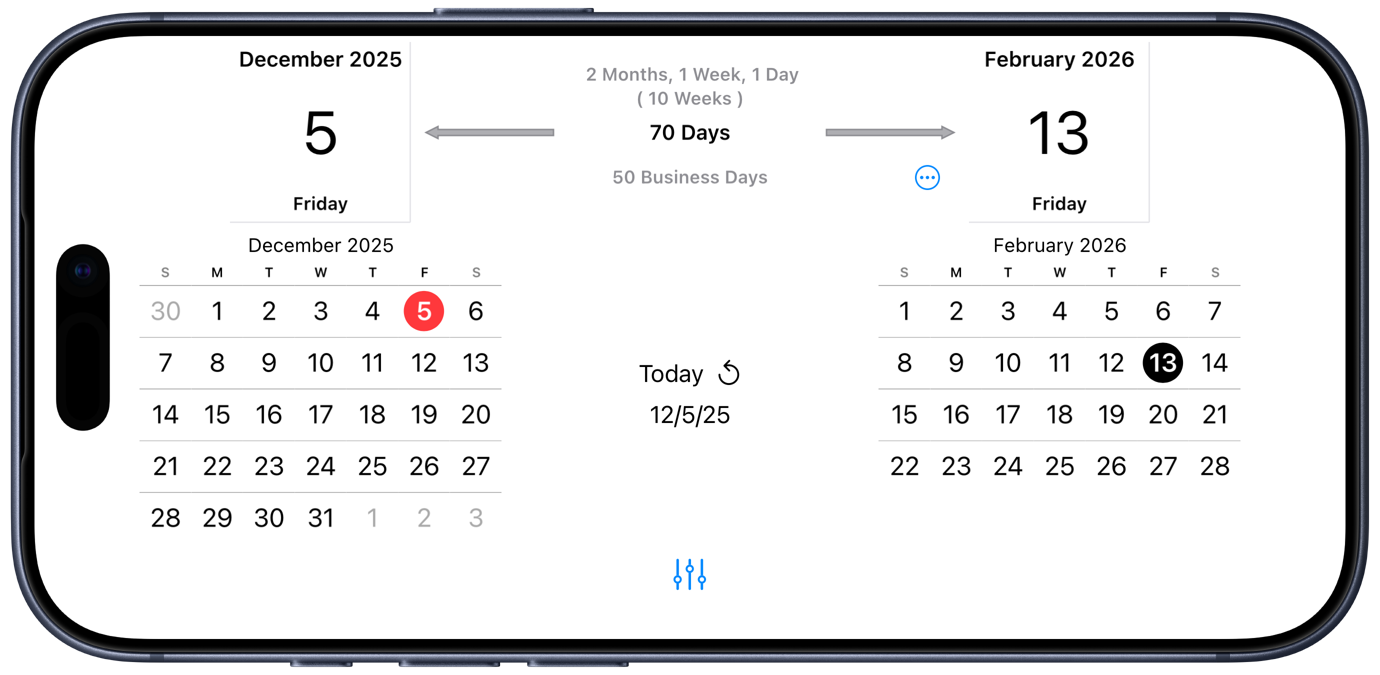
You’ve probably noticed that Time Jump displays the interval in a few different ways: days, business days, and combinations of years, months, weeks, and days. There are settings that let you choose what constitutes a “business day.” It can also show you your calendar entries if you give it permission to do so.
While I was initially put off by Time Jump’s landscape-only orientation, I soon decided that its info-filled layout is worth the inconvenience of turning my phone. Thanks for the tip, sharon!
A sense of structure
November 30, 2025 at 10:45 AM by Dr. Drang
I checked out Practical Approximate Analysis of Beams and Frames from the University of Illinois library a couple of weeks ago. I haven’t dug into it deeply yet, but I smiled in recognition of some of the early material. Here, for example, are some poorly reproduced photos of beams being bent by end loads and moments:
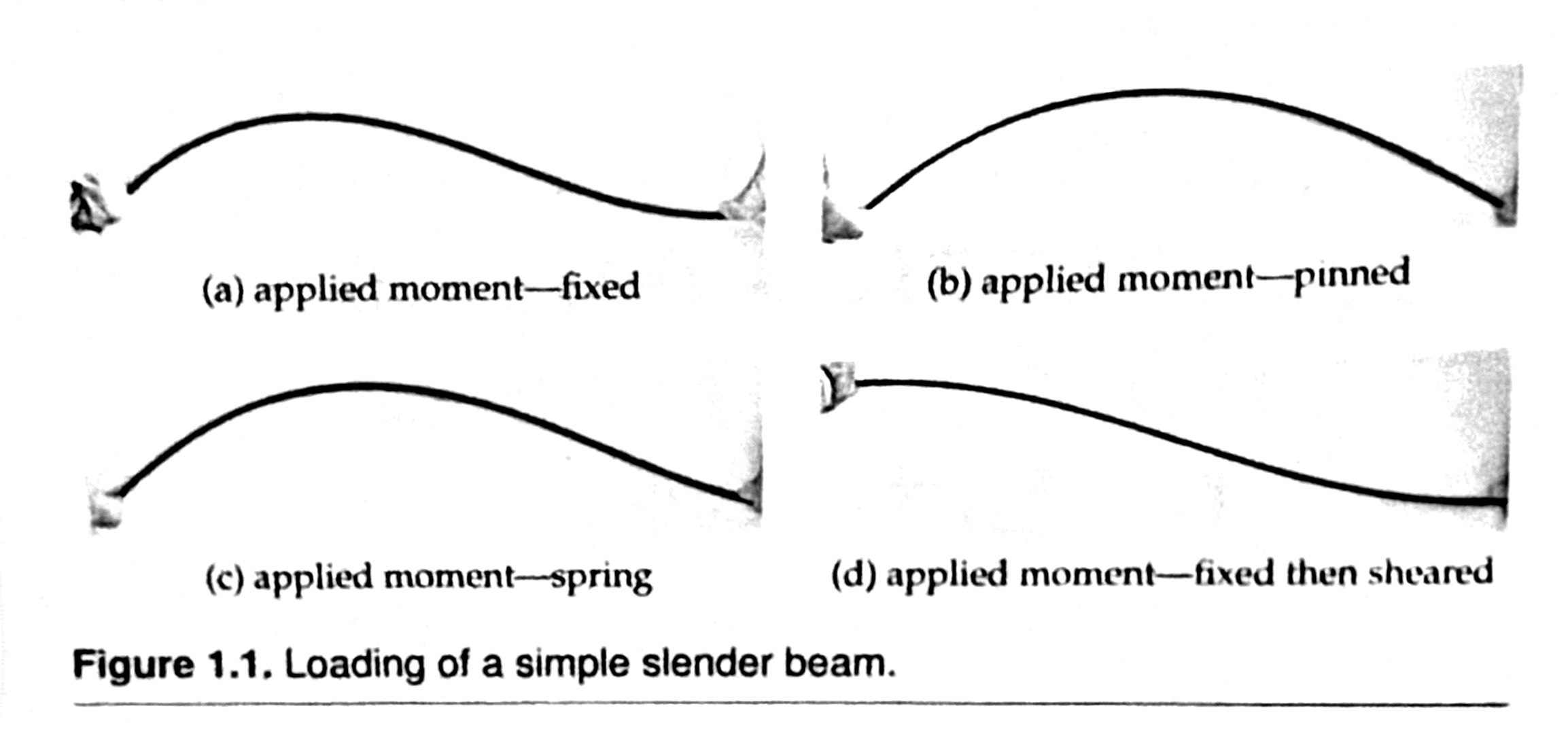
The author uses these photos to explain how the analyst can sketch reasonable approximations to the bent shapes.
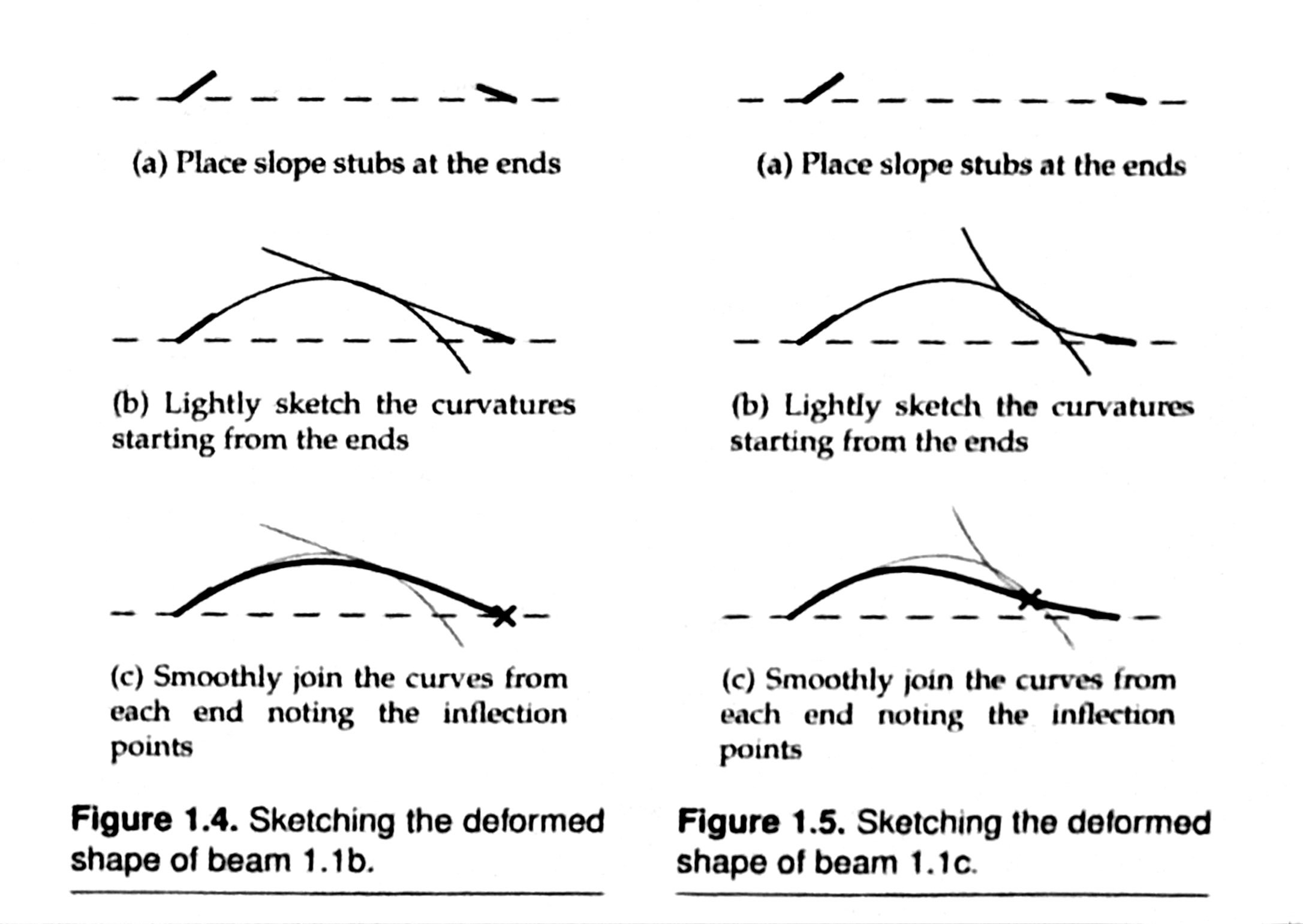
The inflection point mentioned in the (c) subfigure of Figures 1.4 and 1.5 is the point at which the curvature changes from concave down to concave up (or vice versa). This is helpful in analysis because it tells you where the internal bending moment in the beam is zero. Internal bending moments are what determine the important stresses in a beam.
All of my structural engineering professors emphasized the ability to sketch reasonably accurate deflected shapes of the structures we were analyzing, even though we were doing exact1 analysis, not approximate analysis. None were more adamant about this than John D. Haltiwanger, who told us at the beginning of the semester that he would take points off of our homework if it wasn’t accompanied by a good sketch. We all learned that this was not an idle threat and that Prof. Haltiwanger’s standard for “good sketch” was higher than ours. He was my favorite professor as an undergrad.
A few years later, my ability to quickly and accurately sketch the deformed shape of a structure came up during a “pre-prelim” exam. It’s common for Ph.D. candidates to go through a preliminary (or qualifying) exam before moving from the coursework portion to the research portion of their graduate school years. This is essentially a presentation of the proposed research to a small committee of faculty. In theory, the questions asked during a prelim can cover not only the proposed work but any topic in which the candidate had taken a class. The committee members are typically the professors who had taught those classes. Prelims are part of a long tradition of doctoral programs weeding out undesirables.
The Civil Engineering Department at U of I had adopted a further tradition of “pre-prelims.” Before the prelim, the candidate would schedule an hour or so with each member of their committee who would give a short oral exam on the topics covered in class. This made the prelim itself more streamlined, but it also meant that the pre-prelims could be pretty detailed.
My pre-prelim with Arthur Robinson had the following question:
You have a single-story, single-bay 2D frame in which the columns are identical and the beam is prismatic. If a concentrated downward load is placed on the beam to the left of the centerline, which way does the frame sway? Don’t do any calculations, just reason it out.
Let me start by explaining the problem and giving a little background on what everyone in my position would be expected to know. Here’s what the structure and load look like:
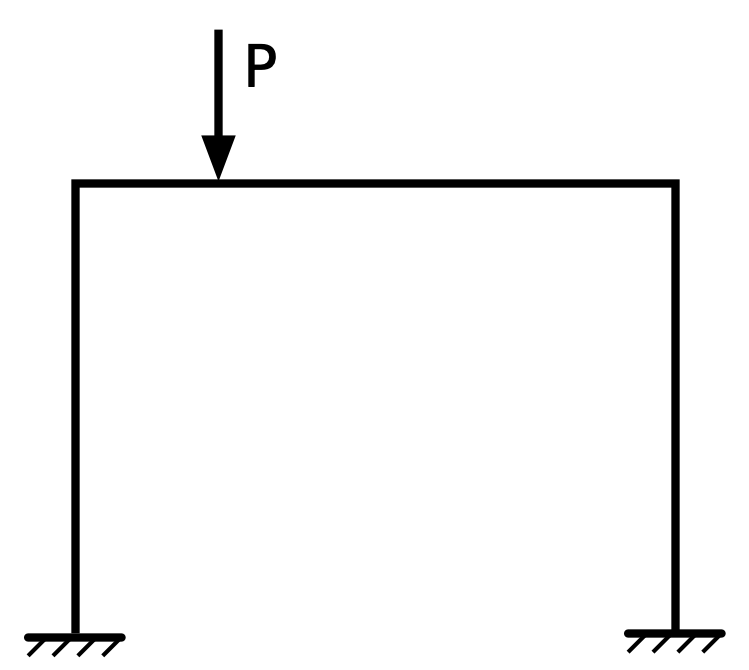
And here are the assumptions we start with:
- Because both the structure and the load are in the plane of the screen, the deformations will also be in that plane. While real structures are always three-dimensional, and most have more than one (vertical) story or (horizontal) bay, this simple structure has many features of more complex structures and is a good pedagogical tool.
- The connections between the beam and the columns are rigid, which means they maintain their 90° angles during the deflection. The connections at the bottoms of the columns can be pinned (free to rotate) or fixed (unable to rotate). The direction of sidesway doesn’t depend on those connections, so I’ll assume they’re fixed. That way I don’t have to draw little hinges at the column bases.
- A prismatic beam is one whose cross-section is constant along its length. A prismatic beam and identical columns makes the frame symmetric about its centerline. If the concentrated load were applied to the center of the beam, the symmetry of the structure and load would lead to symmetric deformation and, therefore, no sidesway. The off-center load is the reason there must be sidesway.
There are at least a couple of ways to solve this problem. One would be to start by considering the directions and relative magnitudes of the bending moments at either end of the beam and work out how those moments affect the deflections of the columns. But this is a grubby sort of solution, and I knew Prof. Robinson wanted something more elegant.
The key is a principle that goes by several names: Maxwell’s Principle, Betti’s Law, and the Reciprocal Relationship are fairly common names, but almost any phrase that includes some combination of Maxwell, Betti, Reciprocal, Law, Relationship, Principle, or Rule will work. The Maxwell is James Clerk Maxwell, the great Scottish physicist known for his much more famous work in electromagnetism. The Betti is Enrico Betti, an Italian mathematician not particularly well known at all.
As a young man, I assumed that the principle in question was discovered first by Betti and independently rediscovered by Maxwell. In my head canon, Maxwell’s name was assigned to it by the English-speaking world in a spasm of Anglocentrism. But that’s wrong. Maxwell got there first with a limited version of the principle that Betti extended and generalized several years later.
Here’s the gist of the principle: We have a structure that is acted upon at different times by two sets of applied loads, called A and B. Each of these sets of loads will generate a deformation in the structure, which we’ll also call A and B. The Maxwell-Betti Reciprocal Principle2 is:
The work done by the A loads acting through the B deformations is equal to the work done by the B loads acting through the A deformations.
To apply this to the problem at hand, we take the original problem statement as A and create a new load and deformation B.
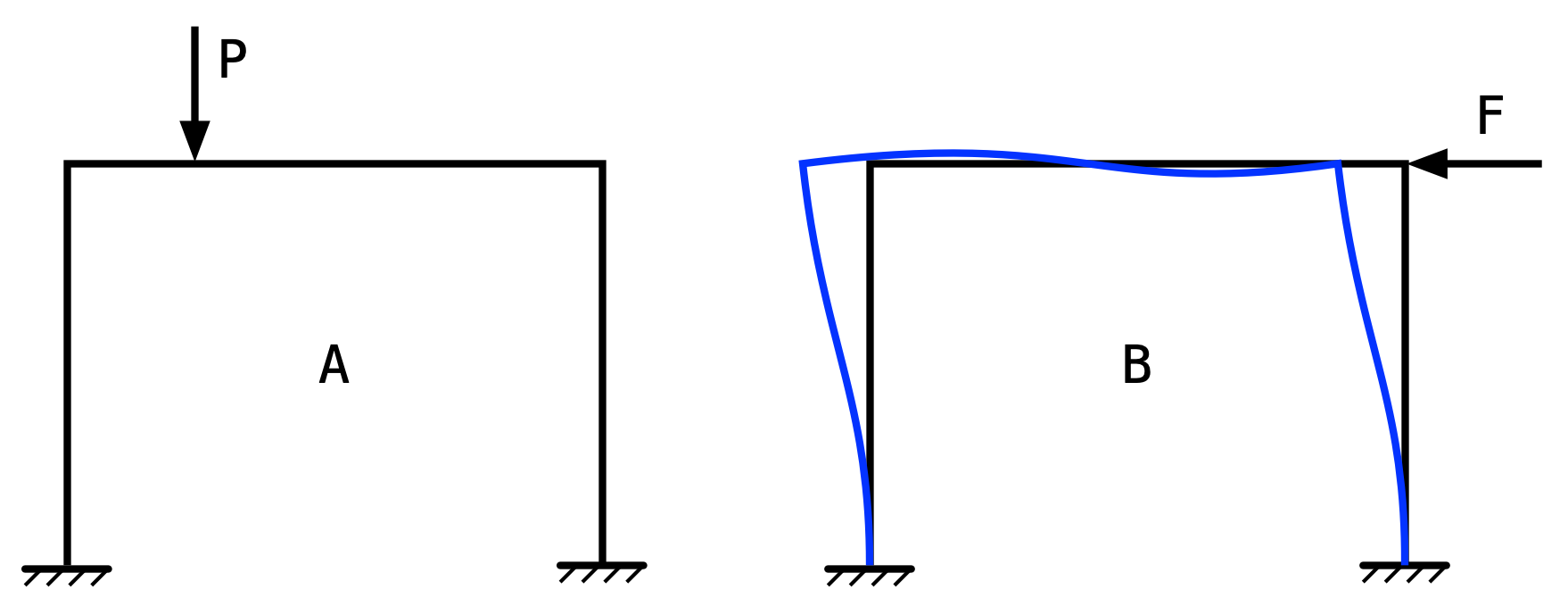
I chose System B to have a horizontal leftward load at the top of the frame, and because Prof. Haltiwanger had pushed me to quickly and accurately draw so many structural deformations, I knew it would deflect into the shape given by the curved blue lines without any calculations.
Reciprocity says that the work done by Load P acting through the deformation of its point of application in System B must be equal to the work done by Load F acting through the sway in System A. Since the left half of the beam in System B deflects up and Load P is down, that work is negative. For the work of Load F acting through the sway of System A to be negative, System A must sway to the right.
Obviously, it didn’t take me this long to explain my solution to Prof. Robinson. He knew where I was going with it as soon as I drew System B on the blackboard. We moved on to his next problem, which I think had to do with the vibrational mode shapes of a system of three masses and springs arranged in a triangle.
(A small confession: grad students talk to each other. Everyone in the department knew that this was one of Prof. Robinson’s favorite problems, so I was prepared for it. I knew the solution on my own, but I certainly wouldn’t have done it as smoothly without the heads-up.)
I don’t remember Prof. Robinson putting any emphasis on drawing deformed shapes in the classes I took from him. He just expected us to be able to do it and to understand the consequences of the shapes we drew. Like in his pre-prelim problem.
