Problem 46

This problem looks more complicated than it is. To show that the weight can move around on the platform without affecting the force transmitted through the short vertical link, we start with the free-body diagram of the platform.

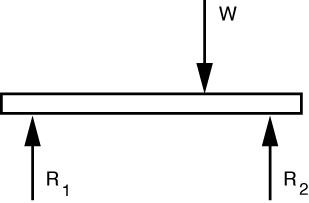
Vertical equilibrium tells us that R_1 + R_2 = W. Exactly how much R_1 and R_2 are depends, of course on how far to the left or right W is. But we won’t worry about that now.

Let’s move on the the FBDs of the triangular levers.

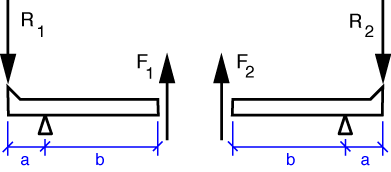
Taking moments about the pivots, we learn that F_1 = R_1(a/b) and F_2 = R_2 (a/b). The force transmitted by the short vertical link is the sum F_1 + F_2 = (R_1 + R_2)(a/b) = W (a/b). So it turns out we’ll never have to worry about exactly where W is; the link force is independent of W’s position.

Moving on to P, we draw the FBD of the lower lever, L_3.

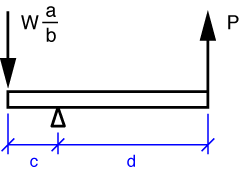
Taking moments about the pivot, we get

P = W \frac{ac}{bd}

Problem 47Problem 45

Last modified: January 22, 2009 at 8:32 PM.

Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

The book

Your host

Problem 46