Den Hartog’s Mechanics

A web-based solutions manual for statics and dynamics

Problem 67

Here, we’re using the second theorem of Pappus in a sort of backwards way: we know the volume of a sphere is \frac{4}{3}\pi r^3 and we know the area of a semicircle is \frac{1}{2}\pi r^2. If we consider our semicircle to be above the x axis as in this figure

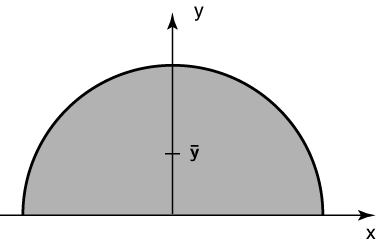
the circumference traversed by the centroid as it’s rotated about the x axis is 2\pi \bar y. So

\frac{1}{2}\pi r^2 \cdot 2\pi \bar y = \frac{4}{3}\pi r^3

and \bar y = \frac{r}{3}.

Problem 68Problem 66

Last modified: January 22, 2009 at 8:32 PM.