Terminal velocity

September 12, 2014 at 12:04 AM by Dr. Drang

I recently read Ancillary Justice, the Hugo and Nebula award winning novel by Ann Leckie and enjoyed immensely, but it had one paragraph that brought me up short. The reason involves fluid mechanics, so it seemed like a good topic for a blog post.

But first the book. Ancillary Justice has a good story, but what hooked me was the way the story is told. The main character and narrator is an artificial intelligence that’s used primarily to run a military spaceship. The AI is shared among hundreds of reanimated corpses that act as the ship’s footsoldiers. The chapters alternate between two time periods about 20 years apart. Using multiple times is a common narrative device, but Leckie layers on other multiplicities.

First, because the narrator has hundreds of bodies, several of the scenes—fighting scenes in particular—are told from multiple points of view by the same narrator simultaneously. Second, as the characters move to different planets with different cultures and languages, they change genders. Their naughty bits and their personalities stay the same, but their perceived role in society flips. In scenes where two languages are being spoken, the gender of a character can change from one sentence to the next.

Leckie handles these shifts in time, position, and gender nicely, leaving you surprised but never confused. There’s also an interesting parallel between the main character and one of her former captains, a regular, non-corpse human who’s been awakened after a thousand years in suspended animation. Leckie’s light touch keeps their relationship interesting.

As for the paragraph that brought me up short, it comes during a scene in which the narrator and her former captain are falling together from a bridge. The narrator, an individual corpse soldier who’s cut off from the main AI, is trying to figure out how to slow the fall and survive.

If I had been more than just myself, if I had had the numbers I needed, I could have calculated our terminal velocity, and just how long it would take to reach it. Gravity was easy, but the drag of my pack and our heavy coats, whipping up around us, affecting our speed, was beyond me. It would have been much easier to calculate in a vacuum, but we weren’t falling in a vacuum.

Maybe this is just a clumsily written passage, but I don’t think so. Leckie isn’t a clumsy writer. As I read it, the “it” of the last sentence can only be either the terminal velocity or the time it takes to reach terminal velocity. But there is no terminal velocity in a vacuum. Objects that fall in a vacuum don’t stop accelerating until they hit the ground. The narrator of the story should know that, but apparently Leckie and her editors don’t.

Terminal velocity is the maximum speed an object achieves while falling through a fluid.¹ When you drop something, gravity pulls it down while the viscosity of the fluid pushes back up. At first, the force of gravity is stronger than the resistance, and the object accelerates. But while gravity remains constant, the viscous resistive force increases with increasing velocity. Eventually, these two forces balance, and the object stops accelerating. It continues its fall at this constant, terminal velocity.

The relationship between velocity and viscous resistive force—called the drag force—is complicated and depends on the nature of the fluid. Generally speaking, in liquids the drag force is proportional to the velocity, while in gases the drag force is proportional to the square of the velocity. Walter Lewin does an excellent job of explaining the two regimes in this lecture from MIT’s Physics I course.

One way to express the drag force, $F_{D}$ , is through this equation:

F_{D} = \frac{1}{2} C_{D} ρ A v^{2}

where $ρ$ is the density of the fluid, $A$ is the cross-sectional area of the object, $v$ is the velocity of the object, and $C_{D}$ is the drag coefficient, which we’ll talk about more in a little while.

When a falling object reaches terminal velocity, the drag force equals the object’s weight. You probably recall from your physics class that weight can be expressed as $m g$ , where $m$ is the mass of the object and $g$ is the acceleration due to gravity.

Setting the two forces equal to one another,

m g = \frac{1}{2} C_{D} ρ A v^{2}

and solving for $v$ gives

v = \sqrt{\frac{2 m g}{C_{D} ρ A}}

This is the expression for terminal velocity.

(Don’t be tempted to do some cancellation with $m$ and $ρ$ to get a volume. The $m$ is the mass of the object and the $ρ$ is the density of the fluid. They have no relationship.)

You might be wondering why we use an equation with just a $v^{2}$ term when we said earlier that for some fluids the drag force is directly proportional to $v$ . The answer lies in how we define the drag coefficient.

Note that we don’t call it the drag constant. That’s because there’s nothing constant about it. It depends on the shape of the falling object and, critically, the velocity of the falling object.

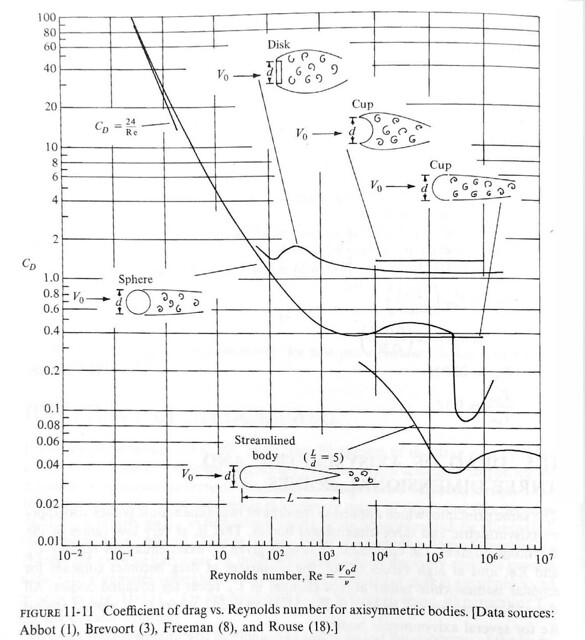
Nowadays, you can go to Wolfram Alpha to calculate the drag coefficient of, for example, a sphere, but when I was a student you’d get it off of graphs that looked like this:

From Engineering Fluid Mechanics by Roberson & Crowe

The horizontal axis is the Reynolds number, one of the many nondimensional numbers you run into in fluid mechanics. Supersonic flight has made the Mach number more well known, but the Reynolds number has more applications in engineering. Using our terminology, it’s defined as

R e = \frac{v d}{ν}

where $d$ is some characteristic cross-sectional dimension (the diameter of sphere, for example) and $ν$ is the kinematic viscosity of the fluid. Low Reynolds numbers are associated with slow movement in viscous fluids, where the fluid flow around the object is laminar; high Reynolds numbers are associated with fast movement and turbulence.

In the upper left of the graph, you’ll see a straight line and the formula $C_{D} = 24 / R e$ . This is the special case of laminar flow around a sphere, the situation covered by Stokes’ Law. If we substitute

C_{D} = \frac{24 ν}{v d}

into our expression for $F_{D}$ and express the cross-sectional area of the sphere in terms of its diameter, we get

F_{D} = \frac{1}{2} \frac{24 ν}{v d} ρ (\frac{π d^{2}}{4}) v^{2} = 3 π d ν ρ v

This is usually written

F_{D} = 6 π μ r v

where we use the radius instead of the diameter and the dynamic viscosity, $μ = ρ ν$ . Either way, you can see that for low Reynolds numbers, the definition of drag coefficient leads us to a result in which the drag force is directly proportional to velocity.

When I was a kid, you’d see examples of Stokes’ Law on TV all the time.

The pearl dropping through Prell was so iconic, commercials in the 70s could just show it without saying a word about it.

How can I be sure this commercial is from the 70s? Just look at Lauren Hutton’s hair at the end of it.

If Stokes’ Law holds, calculating the terminal velocity is pretty easy:

m g = 6 π μ r v

v = \frac{m g}{6 π μ r}

At higher Reynolds numbers, where the flow is turbulent, the calculation isn’t so easy. You have to make a guess at the Reynolds number, get the drag coefficient from the graph, and plug that in to calculate the terminal velocity. Then you have to use that velocity to calculate the Reynolds number to see how good your initial guess was. Chances are, you’d have to adjust your guess and go through the process again.

If you’re on a relatively flat part of the graph, the drag coefficient doesn’t change much with the Reynolds number and your initial guess isn’t so critical. For example, a falling sphere can have a Reynolds number anywhere from 1,000 to 100,000 and the drag coefficient will pretty much stay in the range of 0.4 to 0.5.

Getting back to science fiction, there’s a famous example of terminal velocity in Arthur C. Clarke’s Rendezvous with Rama. One of the expedition party to Rama (a huge and mysterious cylindrical spaceship/world that spins to provide artificial gravity on its inside surface) is stuck on a 500-meter-high cliff and needs to be rescued. The solution is for him to simply jump off the cliff and fall into the ocean below. The artificial gravity is low and so, therefore, is his terminal velocity. He (spoiler alert!²) survives the impact with the water and is picked up by the rest of the crew.

Rendezvous with Rama, like Ancillary Justice, got both the Hugo and Nebula awards. Clarke may have understood physics better than Leckie, but his storytelling isn’t as inventive as hers.

In colloquial English, fluid usually means liquid, but in mechanics a fluid can be either a liquid or a gas. ↩
Speaking of spoiler alerts, The Incomparable podcast talked about Ancillary Justice in two episodes, The Partial Monty and Golem and Jinni Detective Agency. ↩

And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Terminal velocity

Site search

Meta

Recent posts

Credits

And now it’s all this

I just said what I said and it was wrong Or was taken wrong

Terminal velocity

Site search

Meta

Recent posts

Credits

I just said what I said and it was wrong
Or was taken wrong