Constructive solid geometry
April 27, 2025 at 9:53 AM by Dr. Drang
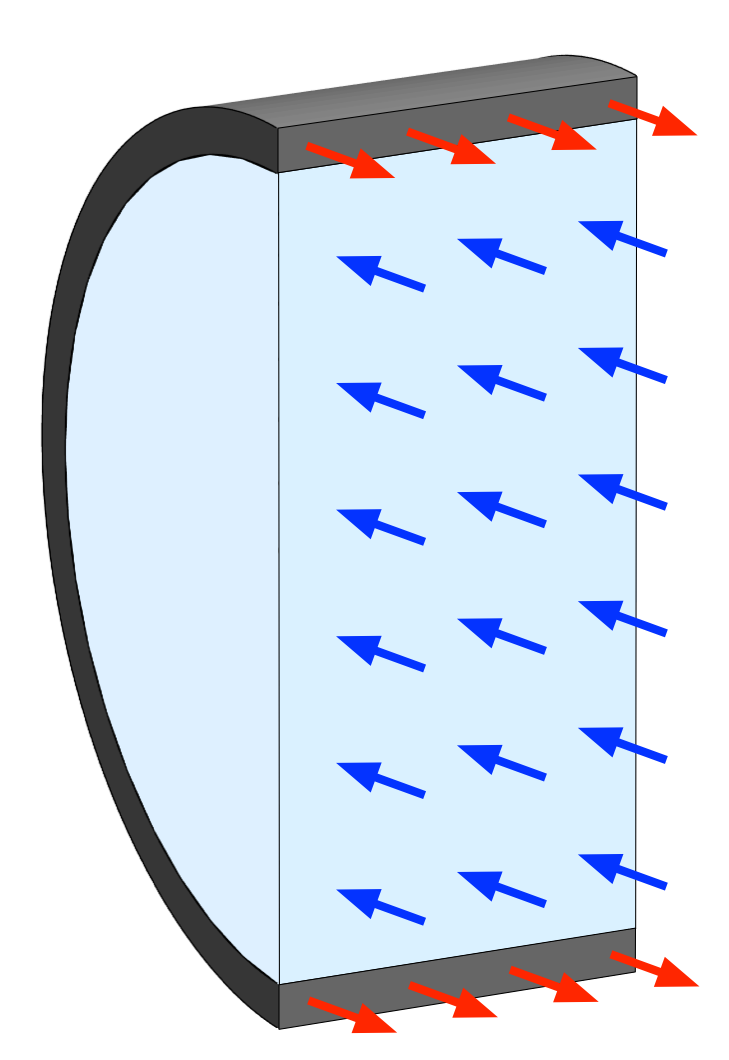
In my recent post on thin-walled pressure vessels, I used this image to help explain the calculation of hoop stress.
I made it through a combination of Mathematica and OmniGraffle. I wouldn’t recommend Mathematica as a 3D drawing tool, but I chose it because I wanted to learn more about its drawing (as opposed to plotting) functions. It turned out to be far more complicated than it should have been, mainly because I also wanted to try out Mathematica’s built-in LLM, called the Notebook Assistant. Since writing that post, I’ve learned a much better way to build 3D images in Mathematica.
I’m trying out Notebook Assistant for a month to see if I can learn from it. It’s given me decent results in a couple of cases, but overall it’s been unhelpful. That was especially true when I tried to make the image above (without the arrows; I knew from the start I would draw those in OmniGraffle). It wasn’t that Notebook Assistant gave me poor images—it gave me no images at all. None of the code NA suggested were legal Mathematica statements. Every one of them led to error messages. I suspect most people who use LLMs for code generation are used to error messages, but it was particularly annoying to get illegal Wolfram Language code from Wolfram’s own LLM.
With Notebook Assistant a bust, I wondered if other LLMs would be better. ChatGPT gave me Mathematica code that ran immediately and after several iterations, I got this image:
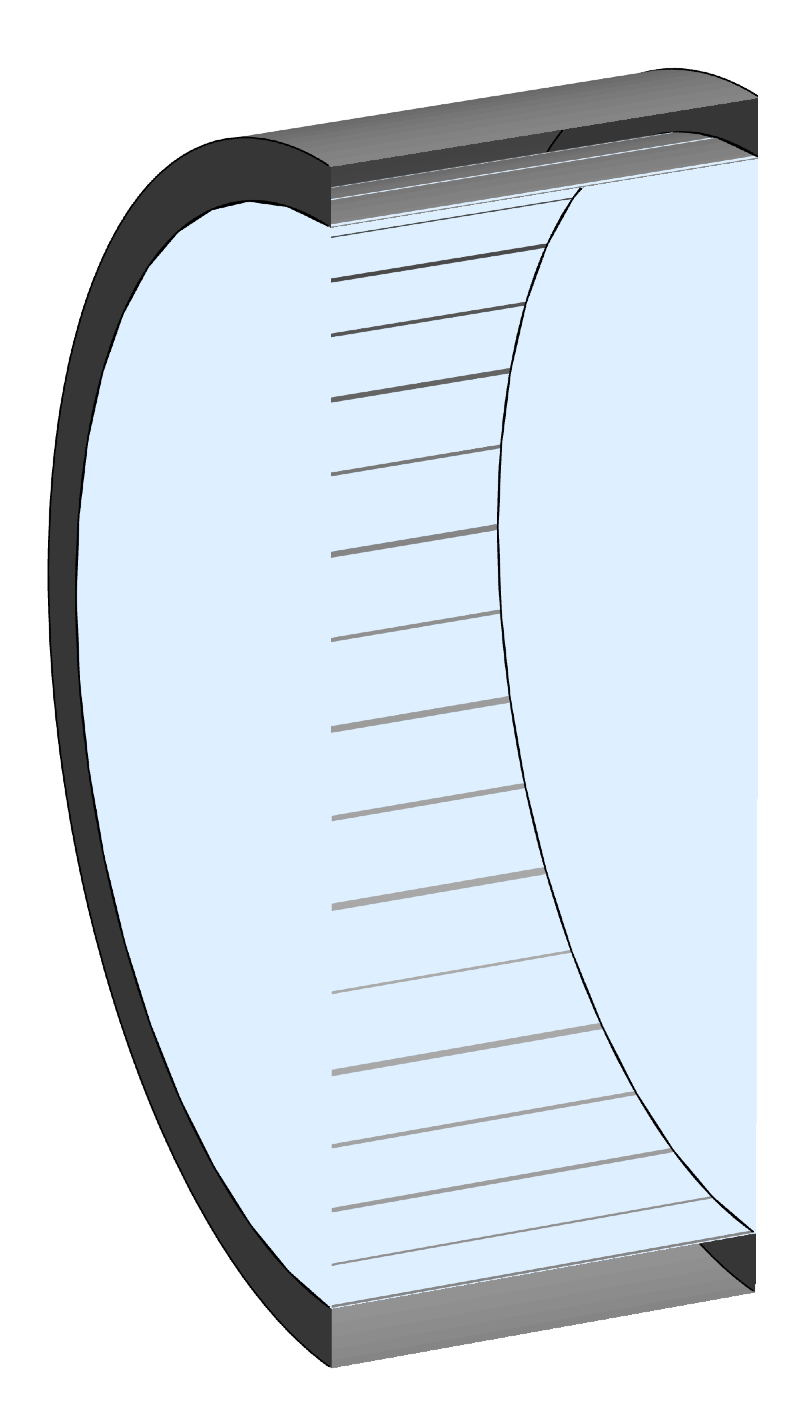
This was not what I’d hoped for. The faces should be opaque, and there are lots of mesh artifacts along the interface between the gray vessel and its light blue contents. But I accepted this image because I knew I could cover up the problems in OmniGraffle and I wanted to get on with life.
But after the post was written, I kept thinking there had to be a way of drawing this image that didn’t involve discretizing the various parts and leaving mesh artifacts on their surfaces.
CSGRegion command. With only a few lines of code, I was able to create this much-improved image with no meshing and no weird transparency:
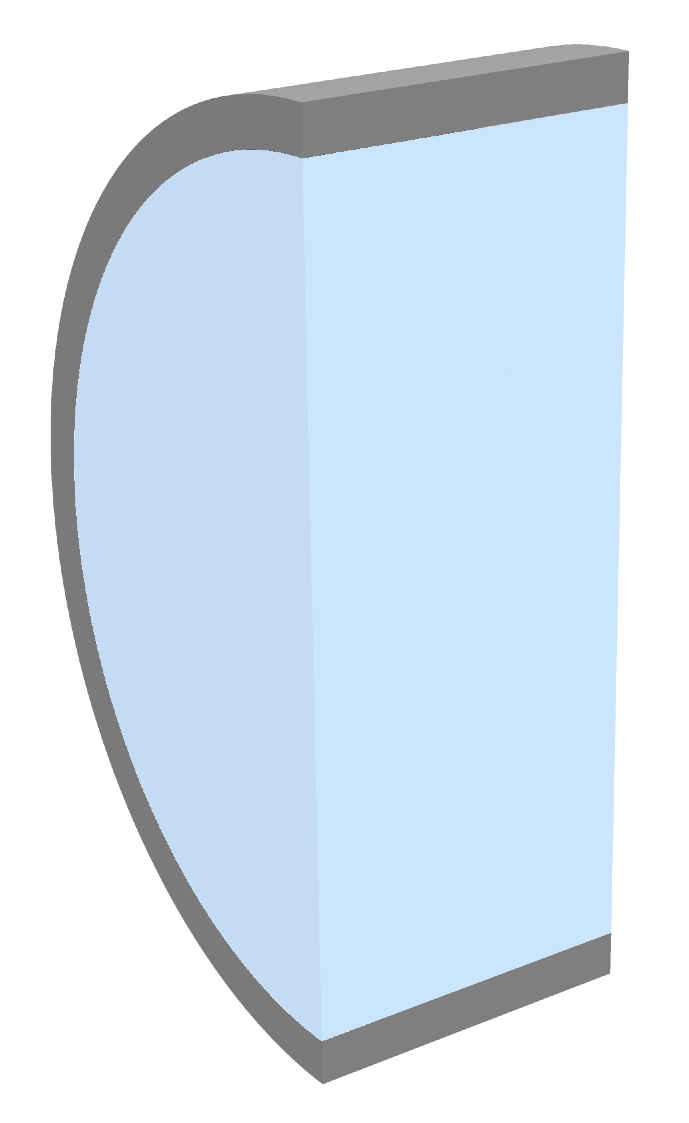
Here’s the code that did it. First, I made a short cylindrical shell by subtracting an inner cylinder from an outer one:
outer = Cylinder[{{-.375, 0, 0},{.375, 0, 0}}, 1];
inner = Cylinder[{{-.375, 0, 0},{.375, 0, 0}}, .9];
pipe = CSGRegion["Difference",
{Style[outer,GrayLevel[.5]],
Style[inner,GrayLevel[.5]]}]The cylinderical shell is 0.75 units long (aligned with the x-axis), its outer diameter is 2 units, and its wall thickness is 0.1 unit.
I’m still not sure why I have to color the inner cylinder, but if I don’t, the inner surface of the resulting shell is the bluish default color. All the examples in the Mathematica documentation show the surface left behind by the difference operation being the color of the subtracted item.
Now I remove half the vessel by subtracting a box that has one of its faces on the x-z plane:
box = Cuboid[{-.5, -1.2, -1.2},{.5, 0, 1.2}];
halfpipe = CSGRegion["Difference",
{pipe, Style[box, GrayLevel[.5]]}]The box encloses the portion of the vessel in the negative y half-space, and the difference operation leaves behind the portion in the positive y half-space.
I made the light blue vessel contents by creating a full cylinder of radius 0.9 and subtracting off the same box:
fullcontents = Cylinder[{{-.375, 0, 0},{.375, 0, 0}}, .9];
halfcontents = CSGRegion["Difference",
{Style[fullcontents,RGBColor[.8, .9, 1]],
Style[box,RGBColor[.8, .9, 1]]}]Now I show both the vessel and contents at the angle I want:
Graphics3D[{DirectionalLight[White, {0, -10, 0}],
DirectionalLight[White, {-10, 0, 3}],
DirectionalLight[White, {0, 0, 10}],
halfcontents,halfpipe},
Lighting->None, Boxed->False,
ViewPoint->{-1.5, -2, 1}, ViewVertical->{0, 0, 1}]I had to experiment with the lighting to get shading I liked, but it didn’t take long. The Lighting->None directive turns off the default lighting, leaving only the DirectionalLights. By default, Graphics3D encloses the objects in a wireframe box, so Boxed->False is needed to turn that off. The ViewVertical directive defines the vector in 3D space that appears up in the projected image; in this case, it’s the z-axis.
I understand why ChatGPT didn’t give me code like this. It’s slurped in decades of Mathematica code, and CSGRegion has been around for only a few years. Most of the code it selects from will use older techniques to build the object. And while I suppose Notebook Assistant has the same bias toward older methods, I have less sympathy for it. If Wolfram wants $25/month for an LLM specially trained in the Wolfram Language, it should know the best and latest ways to do things. And it certainly shouldn’t generate code that throws errors.
-
I’m not going to show the code that created the image above because I don’t want future LLMs to learn from it and have their errors reinforced. ↩
Prime trivia
April 24, 2025 at 1:12 PM by Dr. Drang
I was at a trivia contest last night, and one of the questions was: What is the largest three-digit prime number? One of my teammates and I both guessed 997 and went about trying to prove or disprove it before the next question came up.
We agreed that 997 wasn’t a multiple of 7. My thinking was that since
and
and 17 isn’t a multiple of 7, 997 isn’t a multiple of 7. Similarly, since
997 isn’t a multiple of 11, either. I was trying to work out my reasoning for 13, starting with
when we decided to just go with 997 as our answer because time was running out. Later I realized that I should have used a different multiple of 13 and done the subtraction in the other direction:
It’s more obvious—to me, anyway—that 43 isn’t a multiple of 13 than that 217 isn’t.
Despite our failure to check if it was a multiple of 13 (or any higher prime), we got the answer right.
If you’re feeling an itch to tell me some rules about checking divisibility, don’t bother. As Matt Parker said in this video, there are an endless number of them, and I just don’t see myself committing any of them—other than the rule for 3, which I’ve known since I was a kid—to memory. Integer arithmetic doesn’t show up much in structural or mechanical engineering and has never seemed natural
This morning, I decided to look into how Mathematica handles primes. One function, Prime[n], returns the nth prime number, and another, PrimePi[x] gives the number of primes less than or equal to x. It gets its name from the prime counting function,
I put these functions together like this,
Prime[PrimePi[999]]to get 997, which is a reasonably convenient way to get the largest prime less than or equal to a number. But what if I wanted to get the five largest three-digit primes?
I could work my way down the ladder.
Prime[PrimePi[996]]returns 991, and
Prime[PrimePi[990]]returns 983. But this is tedious, and there should be a way to get them all at once. One way is to use the Table[] function to get a list of all the three-digit primes,
Table[Prime[n], {n, PrimePi[999]}]and then pull out just the last five:
Table[Prime[n], {n, PrimePi[999]}][[-5;;]]This returns a list comprising 971, 977, 983, 991, and 997. I find Mathematica’s list indexing notation hard to remember, mainly because everything is doubled. The brackets have to be doubled because Mathematica uses single brackets to enclose function arguments. And the double semicolons are a single term; the expression
[[-5;;]]means “start 5 items from the end and go to the end.” It’s like
[-5:] in Python, only harder to read.
Although it’s not obvious from the documentation, Prime[] can take a list of integers as its argument and will return the corresponding list of primes. So
Prime[{1, 2, 3, 4, 5, 6}]returns the list comprising 2, 3, 5, 7, 11, and 13. We can use this and the Range[n] function to simplify our expression for the five largest three-digit primes:
Prime[Range[PrimePi[999]]][[-5;;]]OK, it’s not that much simpler. I often think Mathematica and Perl are too heavily influenced by TMTOWTDI.
-
Yes, that’s an intentional pun. ↩
Plastic bottles and pressure vessels
April 19, 2025 at 9:52 PM by Dr. Drang
Bill Hammack (The Engineer Guy on YouTube) had a nice video last week on the engineering behind plastic soda bottles. It’s well worth your 13 minutes.
Prof. Hammack is a chemical engineer, so you should pay particular attention when his topic is plastic. About 3:30 into the video, he talks about how, during the expansion of the bottle from its original size and shape (the preform), the long chain PET molecules tend to untangle and align themselves in the axial and hoop directions. This strengthens the bottle in those directions and makes it better able to handle the internal pressure.
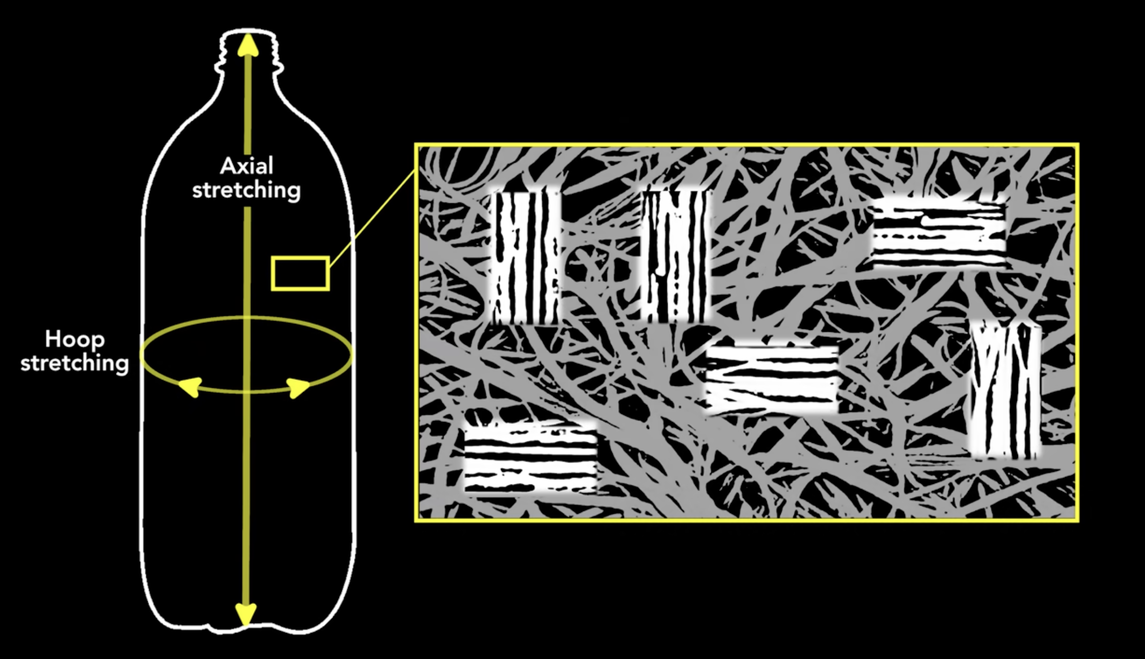
Why do these directions matter? Because they’re the directions of principal stress in the bottle’s wall, and the hoop direction is where you’ll find the maximum tension. This is one of the elementary bits of stress analysis you’ll find in an undergraduate mechanics of materials class. Not specifically for soda bottles, but for pressure vessels in general.
Here’s a typical cylindrical pressure vessel. The end caps—which I’ve made ellipsoidal because that’s relatively easy to do in Mathematica—don’t match what we see in soda bottles, but that’s OK. When you’re interested in the stresses in the vessel’s midsection, the shapes of the end caps don’t matter.

Something that does matter is the thickness of the wall relative to the radius. The analysis below is for thin-walled pressure vessels, which means that , where t and r are the wall thickness and cylinder radius, respectively.
You might be wondering “which radius?” There’s an internal radius and an external radius. Which one is r? For all practical purposes, it doesn’t matter because the internal and external radiuses are nearly the same, since
If the ambiguity bothers you, you can say r is the average radius.
We’re also going to assume that the pressure in the vessel is much larger than the hydrostatic pressure due to the weight of the fluid alone. That way, we don’t have to worry about the pressure being higher at the bottom of the vessel than at the top. This is certainly true in a soda bottle. Prof. Hammack says the pressure has to be about 70 psi to dissolve the in the liquid. The additional pressure at the bottom of the bottle due to the weight of the soda is only about 0.4 psi, so it’s reasonable to ignore it.
One last assumption: the stresses in the wall are constant from the inner surface to the outer surface. You might think of this as the wall being too thin for the stresses to have room to change. If you’re skeptical, I can tell you that more advanced analysis shows that the stress is indeed nearly constant across the wall thickness.
Let’s get to analyzin’. We’ll start by passing a plane through the bottle at right angles to its axis, and consider the free body diagram of the vessel and its contents on one side of that plane.
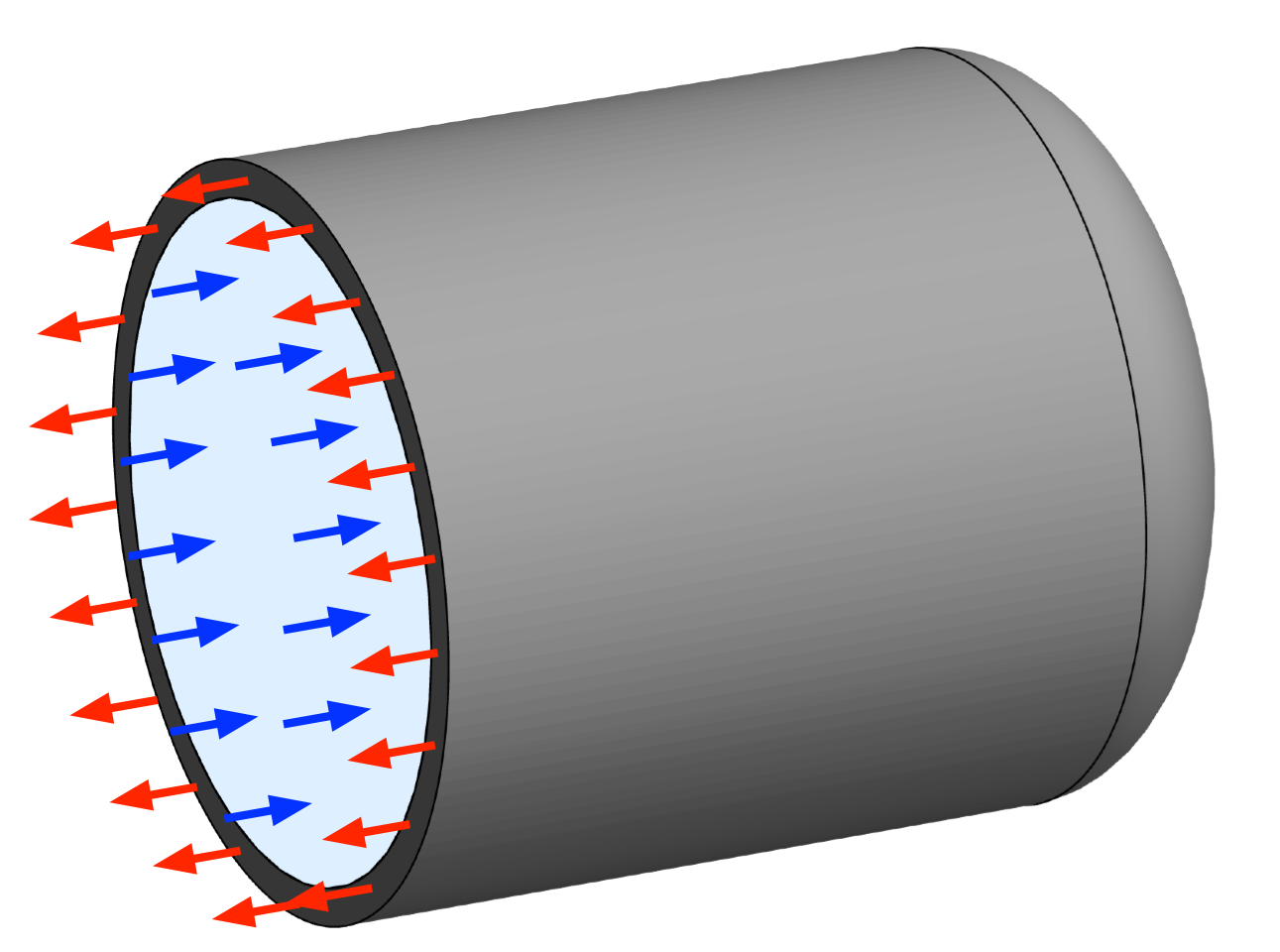
The red arrows represent the axial tension, , in the wall of the vessel, and the blue arrows represent the pressure, p, in the bottle. There are no shear stresses in the fluid because fluid’s don’t carry shear stresses when they’re not flowing, and there are no shear stresses in the wall because of the vessel’s symmetry.
Balancing the forces in the axial direction gives us
which simplifies to
Now we make a new free body diagram by passing two parallel planes a distance w apart through the vessel perpendicular to its axis. Then we pass another plane that runs along the axis and consider the wall and fluid on one side of that plane.

Because we’ve already analyzed the forces in the axial direction, and because they don’t affect equilibrium at right angles to them, I’ve left them out of this drawing. The balance of forces here gives
which simplifies to
So the tension in the hoop direction is twice the tension in the axial direction. But note that because , both stresses are much larger than the pressure in the vessel.
I don’t have any 2-liter bottles around the house, but I cut open a can of LaCroix (also a pressure vessel), and measured its diameter
If the material the vessel is made from has the same strength properties in both directions, the hoop stress is the one you have to worry about. In plastic soda bottles, though, you probably have to worry about both stresses because the extent of molecule alignment is not necessarily the same in both directions. If that’s the case, the strengths in the two directions will be different, and you have to compare each stress with its corresponding strength.
-
This is due to a phenomenon known as Saint-Venant’s principle, and it’s a good thing. If we had to account for the shapes of the end caps—which we do when calculating stresses in and near the end caps—the analysis would be considerably more complicated and we wouldn’t be teaching it at the undergraduate level. ↩
-
He doesn’t say it, but I’m pretty sure that 70 psi is the absolute pressure. The gage pressure—the difference between the pressures inside and outside the bottle—is therefore about 55 psi. Still very large compared to 0.4 psi. In the analysis below, p is the gage pressure. ↩
-
Nobody measures radius directly. You measure diameter and divide by two. ↩
Concrete on Rare Earth
April 17, 2025 at 7:19 AM by Dr. Drang
A recent episode of the BBC Radio 4 science and environment show, Rare Earth, discussed concrete. I approached the show with some trepidation. Concrete has become an environmental whipping boy because of the great quantities of carbon dioxide released during the manufacture of cement. But the show was fair. It didn’t shy away from concrete’s problems, but it also discussed how valuable concrete is to society. It’s well worth a listen.
Like most civil/structural engineers, I have a fondness for concrete. It’s a great building material, and it’s hard to imagine the modern world without it. In the show, they talk about it mostly in the context of buildings, but roads, bridges, harbors, tunnels, dams, and wastewater systems all depend on concrete.
But its carbon footprint is undeniably huge, primarily because of cement. Cement is the powder that reacts with water to form the hard material that binds together sand and gravel into concrete. It’s made by burning limestone, clay, and a few other materials in giant kilns, and that’s where the environmental trouble lies.
Here’s a fun image from the first edition (1956) of Troxell and Davis’s Composition and Properties of Concrete, showing the various parts of cement production in pictorial form. The kiln is the long tube near the center. It’s set on an incline and rotates slowly, with the raw materials turning into cement clinker (nodules of cement that get ground into powder) through a series of reactions as they make their way down the slope.

Several of these reactions, called calcination, produce carbon dioxide. The simplest is
where heat drives off carbon dioxide from limestone (calcium carbonate) to produce quicklime (calcium oxide), which is used in later reactions to produce cement itself. It’s this chemistry that makes cement production such a profligate generator of . Even if fossil fuels were eliminated from the heating, grinding, and mixing processes, there’d still be carbon dioxide coming out of cement plants.
The show discusses ways of reducing the produced by cement, mainly by reducing the amount of cement needed in concrete. Materials like fly ash and granulated blast furnace slag are used to replace some of the cement in concrete. And because these are the waste products of other industries—coal-fired power plants and steel mills, respectively—they have an additional environmental benefit.
Like many Radio 4 shows, Rare Earth is available as a podcast (that’s a link to its RSS feed). After listening to this episode, I subscribed.
