Airplane on a conveyor
January 31, 2008 at 10:06 PM by Dr. Drang
I wasn’t able to watch the end of last night’s Mythbusters, but I take it that they got the airplane to take off from an opposite-moving conveyor belt. Not surprising. Also not surprising is that people are still arguing about it. Part of the arguing seems to be based on different interpretations of the problem. Let’s walk through the problem step by step and look at the consequences of the different interpretations.
I’ll start by saying that I have a Ph.D. in engineering and that I used to teach mechanical engineering at a major US university. Further, I taught statics and dynamics courses, the very courses that deal with the issues at hand. This will, of course, mean nothing to the great self-appointed experts of the internet, but I think it’s worth a mention. Onward.
There are three things about the problem setup that everyone seems to agree on. First, there is a speed, call it v0, that the airplane needs to achieve to take off from a normal, stationary runway. Second, the top surface of the conveyor is set to move at this same constant speed, v0. Third, the airplane is placed on the conveyor with its nose pointing in the direction opposite the motion of the conveyor. (I.e., if the top surface of the conveyor is traveling south, the plane is pointed north.)
At this point there’s a fork in the way people interpret the problem. You can assume:
- The engine speed of the plane on the conveyor is set to the same speed as it would be when taking of from a normal runway, which means that the propellor is producing the same thrust. This will lead to an airplane body speed (or wing speed) of v0 relative to the ground and the surrounding air. Since it is the wing speed relative to the air that produces lift, the plane will take off. This is what the Mythbusters assumed and is how they set up their tests.
Or you can assume:
- The body speed of the plane relative to the conveyor is set to the normal takeoff speed, v0. This will lead to a wing speed of zero relative to the ground. There will be no lift and the airplane will not take off. It turns out, though, that the engine speed needed to achieve this body or wing speed is much, much less than the engine speed needed for a normal takeoff.
I suspect that a lot of people think you can have it both ways: an engine speed equal to that of normal takeoff and a body speed of v0 relative to the conveyor. That, in fact, is the trick of the problem. But you can’t have it both ways.
Here’s a side view of an old biplane that I lifted from this site. I’ve added the arrows that represent the forces that act on the plane as it’s trying to take off. This sort of drawing is called a free body diagram and is one of the fundamental tools for solving mechanics problems.
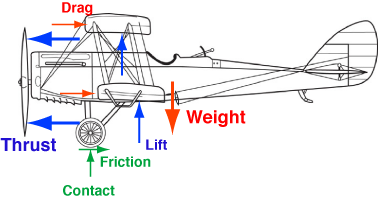
If we assume the first scenario, with the engine speed equal to that of a normal takeoff, the thrust will be much higher than the sum of the drag and friction forces, and the plane will accelerate to the left. (The friction force won’t increase much as the speed increases and won’t be significantly different from the friction in a normal takeoff.) Eventually, the plane will reach a speed relative to the ground and air where the lift forces at the wings will be greater than the weight. At this point, the contact force will drop to zero and the plane will take off.
If we assume the second scenario, with the body speed of the plane relative to the ground and the air of zero, the drag force will be zero (because the wings won’t be moving relative to the air). Since the plane is stationary relative to the ground, its horizontal acceleration is zero and its horizontal forces must be balanced. Therefore, the engine will only have to provide enough thrust to balance the relatively small friction at the wheels. This is much less thrust than is required for the first scenario, so the engine speed will also have to be much less than in the first scenario.
The upshot is you can’t have a stationary plane with its engine running like it would for a normal takeoff. You have to pick one or the other.
[Those of you familiar with free body diagrams may take issue with where I’ve placed some of the forces. Me too. I know the moments aren’t in balance, but I wanted to keep force arrows separated enough to be easy to distinguish. If moment equilibrium were important to the problem I’d be more careful where I drew the arrows.]
If you’re wondering why the thrust is forward rather than backward, the explanation is that while the propellor is pushing back on the air, the air is pushing forward on the propellor. Newton’s third law. It’s the same reason you’re able to walk forward: your feet push back on the ground and the ground pushes forward on your feet.

