Next post Previous post

An application of Castigliano's Second Theorem with Octave

October 24, 2009 at 5:53 PM by Dr. Drang

This week I did an analysis of a set of leaf springs and found myself using a favorite technique that I seldom get to apply anymore: Castigliano’s Second Theorem. There is some real, though not especially difficult, math ahead, so if you come here for the little Mac-based scripts I typically write you may want to skip this one. If you do want to follow along, I suggest you visit this page and download one of the TeX font packages there. This page, and the other pages in which I use Davide Cervone’s wonderful jsMath system, will load faster and print better if you have those fonts on your computer.

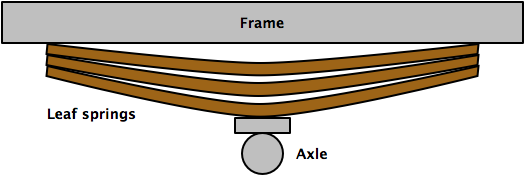
First, let’s talk about leaf springs. Leaf springs are long, flat steel strips bundled together to provide part of the suspension system of heavy vehicles like trucks. They sit between the axle and the frame and smooth out the ride by flexing. You can think of them as allowing the body of the vehicle to bounce above the axle (roll your mouse over the images to see the springs flex),

or you can think of them as allowing the axle to bounce up toward the frame as the vehicle goes over bumps in the road.

In fact, the usual behavior is a combination of the two, but since we will be investigating the spring stiffness—a static property—the analysis is the same no matter which frame of reference you choose.

In some leaf spring packages, the individual leaves are curved to nestle against one another; in others, like the kind I dealt with this week, the leaves are curved to meet only at the center and at the tips, as in the simplified schematic drawings above.

To determine the stiffness of a spring package like that in the drawing, each leaf can be treated as a simply-supported beam with a central point load, and the stiffnesses of the package is the sum of the stiffnesses of the individual leaves. Because the initial curvatures of the leaves are relatively small (the ratio of leaf thickness to initial radius of curvature is much less than one), we can treat them as straight beams with no significant error.

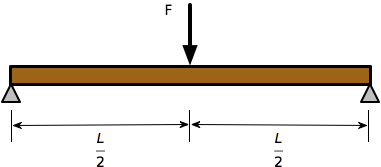
The deflection under the load of a simply-supported beam of uniform thickness and width loaded at the center is

Δ=FL348EI\Delta = \frac{F L^3}{48EI}

where E is the modulus of elasticity of the steel (29,000,000 psi in US Customary units), and I is the area moment of inertia of the cross section,

I=bt312I = \frac{b t^3}{12}

for a rectangle of width b and thickness t. The equivalent spring stiffness, k, is the ratio of load to deflection, so

k=FΔ=48EIL3=4Ebt3L3k = \frac{F}{\Delta} = \frac{48EI}{L^3} = \frac{4Ebt^3}{L^3}

Repeat this calculation for each leaf, add them up, and you get the equivalent spring stiffness for the package. Very simple if you have leaves of uniform thickness.

Unfortunately, the leaves I was analyzing were tapered, about twice as thick in the center as out at the tips. It’s because there is no simple formula for a tapered beam that I went to Castigliano’s Second Theorem.

Carlo Castigliano was a 19th-century Italian mathematician/physicist/engineer who studied at the Polytechnic of Turin. His dissertation presented the two theorems that bear his name. The First Theorem is interesting but doesn’t have a lot of practical application. Castigliano’s Second, though, is very helpful in solving many interesting real-world problems in structural and mechanical engineering. Including, as I said at the top, the problem of the tapered beam.

Castigliano’s Second Theorem states that the derivative of the complementary strain energy of a body with respect to a point load acting on that body is equal to the deflection, in the direction of the load, of the point on the body to which the load is applied. In mathematical terms, this is

∂U*∂F=Δ\frac{\partial U^*}{\partial F} = \Delta

A trivial demonstration of this can be found in the behavior of a simple linear spring. The complementary strain energy in the spring, U*U^* is the area above the usual force-deflection diagram, written in terms of the applied force and the spring stiffness. Recall that the regular strain energy, UU, is the area below the force-deflection diagram, and is written in terms of the deflection and the spring stiffness.

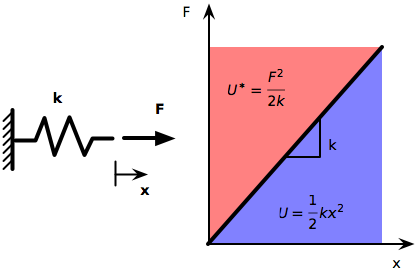
According to Castigliano’s Second, the deflection of the spring is

Δ=∂U*∂F=∂∂F(F22k)=Fk\Delta = \frac{\partial U^*}{\partial F} = \frac{\partial}{\partial F}\left(\frac{F^2}{2k}\right) = \frac{F}{k}

which is exactly what we expect. The genius of Castigliano was his generalization of this trivial case to any type of structure.

Update 10/25/09
I meant to add here that the strain energy and the complementary energy are equal for a linear elastic spring, but would not be equal for a nonlinear spring.

To apply Castigliano’s Second to our tapered beam problem, we’re going to first take advantage of the symmetry of the beam and analyze just the left half. The right half will behave as a mirror image of the left, so once we’ve analyzed the left half, we have the solution for the right half.

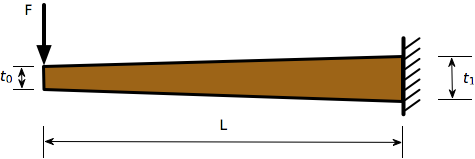
The left half acts like a cantilevered beam, as shown in the diagram below. The complementary strain energy of a beam in bending is governed by this equation:

U*=∫0LM22EIdxU^* = \int_0^L \frac{M^2}{2EI} dx

where M is the bending moment in the beam due to the applied force. Both M and I are functions of x,

M=FxM = Fx I=b(t0+αx)312I = \frac{b (t_0 + \alpha x)^3}{12}

where α=(t1−t0)/L\alpha = (t_1 - t_0)/L is the rate at which the thickness increases as we move from the tip to the wall. Thus,

U*=∫0LF2x22Eb(t0+αx)312=6F2Eb∫0Lx2(t0+αx)3dxU^* = \int_0^L \frac{F^2 x^2}{2 E \frac{b (t_0 + \alpha x)^3}{12}} = \frac{6 F^2}{E b} \int_0^L \frac{x^2}{(t_0 + \alpha x)^3} dx

Putting this into the Castigliano equation, we get

Δ=∂U*∂F=12FEb∫0Lx2(t0+αx)3dx\Delta = \frac{\partial U^*}{\partial F} = \frac{12F}{Eb} \int_0^L \frac{x^2}{(t_0 + \alpha x)^3} dx

Back when I was a student, we didn’t have all these fancy personal computers, so we’d have to do that integral analytically, probably through integration by parts. Now I can’t be bothered. I just fire up Octave, enter the values, and let it do the integration numerically. Here’s my Octave session for a particular set of tapered beam dimensions (I used Octave’s diary command to save the session as a text file):

octave-3.2.3:2> global E=29e6 b=3 t0=.5 t1=1 L=25;
octave-3.2.3:3> function retval = A(x)
> global t0 t1 L;
> retval = x^2/(t0 + (t1-t0)/L*x)^3;
> endfunction
octave-3.2.3:4> [int,icode,nfun,err] = quad("A",0,L)
int =  8518.4
icode = 0
nfun =  21
err =  9.4573e-11
octave-3.2.3:5> k = E*b/12/int
k =  851.10

So the stiffness of one-half of a leaf is 851 lb/in, which makes the stiffness of the full leaf 1702 lb/in. Compare this to

4·29,000,000·3·13503=2785lb/in\frac{4\cdot29,000,000\cdot3\cdot1^3}{50^3} = 2785\: \textrm{lb/in}

for a 1″ flat leaf, and

4·29,000,000·3·0.53503=348lb/in\frac{4\cdot29,000,000\cdot3\cdot0.5^3}{50^3} = 348\: \textrm{lb/in}

for a 0.5″ flat leaf. How close would we have come if we’d used the flat-leaf formula with the average thickness? We’d get

4·29,000,000·3·0.753503=1174.5lb/in\frac{4\cdot29,000,000\cdot3\cdot0.75^3}{50^3} = 1174.5\: \textrm{lb/in}

which underestimates the stiffness by more than 30%. Another way to think of this is that by tapering the beam from 1″ to ½″ we get 30% more stiffness for the same amount of steel as a flat beam of ¾″.

For the purposes of this post, I made the taper linear, which allowed me to use Octave’s quad function for integration. In fact, the leaf thickness tends to vary in a more complicated way, so the more general way to solve the problem is to

  1. Express the thickness as a vector of values uniformly-spaced along the length of the spring.
  2. Use Octave’s many matrix/vector operators to generate a vector of the integrand.
  3. Use the trapz function to perform the integration.

It takes a bit longer to do it this way because there are more thickness values to enter, but conceptually it’s the same problem.

The tapered leaf spring problem is tailor-made for Castigliano’s Second Theorem.

When you run into a problem with these characteristics, it’s good to have Castigliano in your toolbox.

Tags:

Next post Previous post