Next post Previous post

Aye-aye, capstan

April 16, 2010 at 10:58 PM by Dr. Drang

My fourth-grade son’s gym class is doing rock-climbing, and this morning I was at the school, acting as an adult belayer. The belaying system in the gym uses a simple rope friction arrangement, the principles of which are commonly taught to undergraduate engineers under as the belt friction problem or the capstan problem.

As a child climbed the rock wall, he wore a harness that was attached to a safety rope. The safety rope was wrapped around a pipe mounted at the ceiling, with the rope going around the pipe one full wrap and then between 150° and 180° more. The other end of the rope went through a belaying device1 hooked into the gym floor and was controlled by one of the adult helpers.

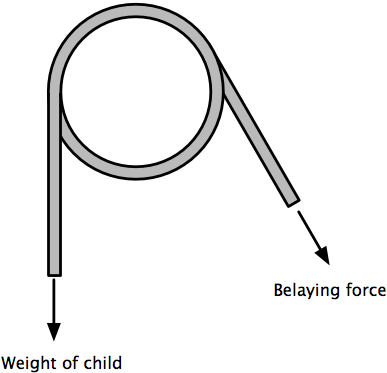
The belaying force is the force necessary to support the weight of the child when he lets go of the rock wall to be lowered back to the floor and is much less than the weight being supported. For this simple wrapped-rope setup, it turns out to be pretty easy to calculate the belaying force.

Start by considering a small section of the rope in contact with the pipe, extending over the arc dθd\theta. Four forces act on this little piece of rope:

  1. The tension at one end of the piece, TT.
  2. The tension at the other end, T+dTT + dT.
  3. The outward normal force that the pipe exerts on the rope, NN.
  4. The friction force acting to resist slipping of the rope, ff.

When the rope is on the verge of slipping, f=μNf = \mu N, which is a common way of expressing Coulomb’s law of friction.2 The dimensionless constant μ\mu is the friction coefficient.

Here’s a free-body diagram of our little piece of rope.

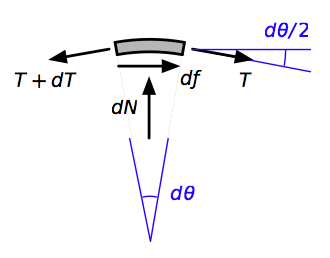
Equilibrium in the horizontal direction is governed by the equation

∑Fx=Tcosdθ2−(T+dT)cosdθ2+df=0\sum F_x = T \cos\frac{d\theta}{2} - (T + dT)\cos\frac{d\theta}{2} + df = 0

and equilibrium in the vertical direction is governed by

∑Fy=dN−Tsindθ2−(T+dT)sindθ2=0\sum F_y = dN - T \sin\frac{d\theta}{2} - (T + dT) \sin\frac{d\theta}{2} = 0

Since dθd\theta is vanishingly small, we can say

cosdθ2=1andsindθ2=dθ2\cos\frac{d\theta}{2} = 1 \quad \textrm{and} \quad \sin\frac{d\theta}{2} = \frac{d\theta}{2}

Making these substitutions, dividing through by dθd\theta, and doing a bit of simplification, we get

dTdθ=dfdθ=μdNdθ\frac{dT}{d\theta} = \frac{df}{d\theta} = \mu \frac{dN}{d\theta}

and

dNdθ=T\frac{dN}{d\theta} = T

Combining these two equations, we get the linear differential equation

dTdθ=μT\frac{dT}{d\theta} = \mu T

the solution of which is

T=T0eμθT = T_0 e^{\mu \theta}

where T0T_0 is the tension in the rope at the end that’s trying to prevent slipping. In our case, that’s the belaying force. If you know the high force and want to solve for the low force, you can flip the equation around,

T0=Te−μθT_0 = T e^{-\mu \theta}

As is always the case when angles appear in the solution of a differential equation, we’ll have to express the total wrap angle, θ\theta, in radians rather than degrees. Let’s use the small of the range, one wrap plus 150°, which is

2π+5π6=17π6=8.902\pi + \frac{5 \pi}{6} = \frac{17 \pi}{6} = 8.90

Now we need the friction coefficient. This is never as straightforward as undergraduate engineering texts lead you to believe. A lot of really complicated surface physics is being hidden behind that single constant, μ\mu, and handbooks almost always present friction coefficients as ranges rather than single numbers. The Handbook of fibre rope technology by H. A. McKenna, J. W. S. Hearle, and N. O’Hear provides this table of typical friction coefficients between different rope materials and steel.

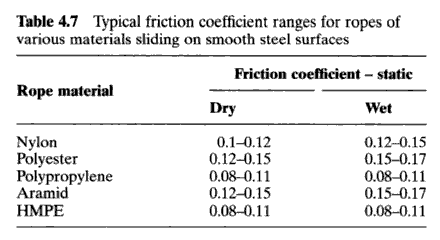
The pipe in the gym was not smooth steel, it had a black oxide coating which probably increased the friction coefficient a bit. I’m going to use a value of 0.20, although the calculation could be easily redone with another value.

For a 75 pound child, the belaying force needed to prevent the rope from slipping around the pipe is

T0=75e−(0.20)(17π/6)=12.6lbT_0 = 75 e^{-(0.20)(17\pi/6)} = 12.6\:\textrm{lb}

which is just 17% of the suspended weight. That’s why it’s easy to control.

Because the wrap angle is in the exponent, the tension difference across a capstan can be tremendous. For example, if the rope in my son’s gym had been wrapped one more time around the pipe, the belaying force would have dropped to just

T0=75e−(0.20)(29π/6)=3.6lbT_0 = 75 e^{-(0.20)(29\pi/6)} = 3.6\:\textrm{lb}

which isn’t much different from the weight of the rope hanging down on the belaying side. It would have been almost impossible to lower a child with the extra wrap.

I’m not sure when the capstan problem was first solved mathematically, but the great mechanical advantage that can be gained by wrapping a rope around a post or a cleat has been known to sailors for millennia. Another familiar use is on the tuning pegs of stringed instruments.

In case you’re wondering, I was paying attention to the kids while I was belaying—I didn’t just stare at the rope and think about the capstan problem.

But I did stare enough to be able to write this post.

  1. Similar to a Petzl Grigri, which also uses friction through a cam arrangement, but which I won’t be discussing here. ↩

  2. Yes, it’s the same Coulomb whose name is used for the standard unit of electrical resistance charge. ↩

Next post Previous post