Next post Previous post

A physicist walks into a bar

June 18, 2010 at 12:20 AM by Dr. Drang

A few weeks ago, a mathematician blogger wrote a post in which she considered the effect of friction on a rope wrapped around one or more poles. A physicist blogger then took up the idea and ran some experiments. Some of their readers pointed out my article on the same topic. So we have a mathematician, a physicist, and an engineer all blogging about the same topic, which sounds like the set up for a joke.

If you’re not a mathematician, physicist, or engineer, you may never have heard one of these jokes. They’re certainly not as popular as the “priest, rabbi, and minister” jokes, but like the clergyman jokes, the MPE jokes work off of stereotypes:

  1. Mathematicians are really smart, but are out of touch with the real world.
  2. Physicists are always seem to be testing things.
  3. Engineers are practical but kind of dumb.

What does this have to do with blog posts about rope friction? Well, if you read the posts, we all played to the stereotype:

  1. The mathematician was mostly interested in the idea of rope friction being multiplicative and how that related to the more general idea of logarithms.
  2. The physicist ran a series of tests and decided that rope friction was multiplicative—at least to within experimental error.
  3. The engineer just wanted to make sure some third graders didn’t fall off a rock wall. Also, he looked up the solution in a book and consulted a table of values, which fits the behavior in the “red rubber ball” joke.

By the way, the mathematician was right: the effect of multiple poles is multiplicative rather than additive, and here’s why:

Recall from my earlier post that when a rope is wrapped around a pole and is on the verge of slipping, the ratio between the large force and the small force is

FmaxFmin=eμθ\frac{F_{max}}{F_{min}} = e^{\mu\theta}

where θ\theta is the angle of wrap (in radians), and μ\mu is the coefficient of friction between the rope and the pole.

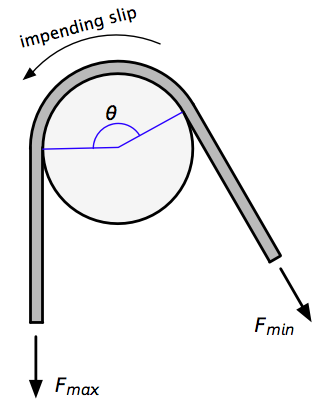
Let’s now look at the two-pole problem. A rope is wrapped around the first pole by an amount θ1\theta_1 and around the second pole by θ2\theta_2. We’ll call the large force that’s trying to get the rope to slip F3F_3 and small restraining force F1F_1. We’ll call the tension in the section of rope between the poles F2F_2.

Here’s the arrangement, where I’ve split the rope between the pole to show the tension in that section.

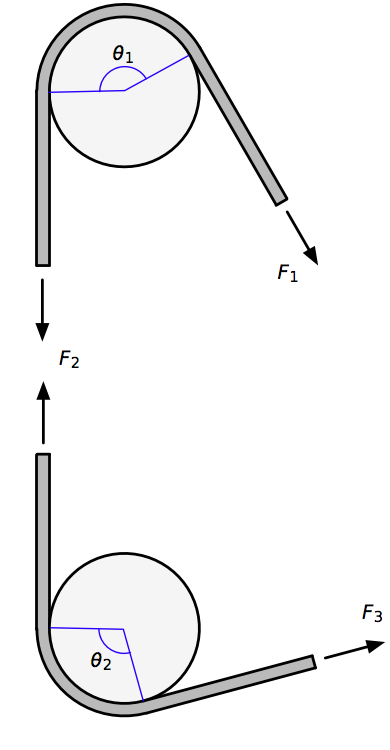
From our previous work, we know that

F2F1=eμθ1\frac{F_2}{F_1} = e^{\mu\theta_1}

and similarly

F3F2=eμθ2\frac{F_3}{F_2} = e^{\mu\theta_2}

Therefore,

F3F1=F2F1F3F2=eμθ1eμθ2\frac{F_3}{F_1} = \frac{F_2}{F_1} \frac{F_3}{F_2} = e^{\mu\theta_1}e^{\mu\theta_2}

which is clearly multiplicative. The extension to three or more poles is, I think, obvious. More interestingly, we can use the properties of exponents to simplify this further,

F3F1=eμθ1eμθ2=eμ(θ1+θ2)\frac{F_3}{F_1} = e^{\mu\theta_1}e^{\mu\theta_2} = e^{\mu (\theta_1 + \theta_2)}

which means that the effect of wrapping the rope around two poles could be achieved by wrapping it around just one pole by the sum of the two angles. (Note that we’ve assumed the friction coefficient to be the same for both poles.)

The physicist1 comes to this conclusion after running his tests, but he has to stretch the idea of experimental error pretty far to do so. Friction is a tricky thing to measure because the system has to be on the verge of slipping as you measure the forces. Frankly, I don’t think his test setup allows for that. He attaches force gauges to either end of a rope and has one of them clamped down as he pulls with the other. I just don’t see how he can ensure that the rope is on the verge of slipping as the data are collected.

More bothersome than the test setup is this statement at the end of his post:

The normal model for friction says that the frictional force is proportional only to the force the two surfaces are pushing against each other. Not sure if that works here.

Yes, the normal model (i.e., Coulomb friction) definitely works here. It’s how you derive the formula for the relationship between the forces, and it’s the reason the behavior is multiplicative. And because this is an elementary application of mechanics (even dumb engineers learn how to do it as undergrads), I’m surprised a professor of physics hasn’t been exposed to it.

  1. Yes, of course these people have names: the mathematician is Sue VanHattum and the physicist is Rhett Allain. I just think it’s funnier to refer to them the way it’s done in the MPE jokes. ↩

Next post Previous post