Bathroom scales and Robert Hooke
July 6, 2010 at 8:00 AM by Dr. Drang
A few weeks ago I had an argument with our bathroom scale, and it got me thinking about strain gauges and Robert Hooke.
The argument with the scale came about because it wouldn’t give me a straight answer. I’ve been weighing myself every day since the beginning of the year and recording it in a Simplenote document on my iPhone (the reasons for doing this are explained here). The scale is a digital Thinner scale from Conair with a nice big LCD display I can read without my glasses.

I got into the habit of weighing myself a few times each morning because the first weight was usually not reliable. I’d get on the scale, note the weight, then get off and back on again and see that the second weight was different. So I decided to only record weights that were repeatable. Usually this meant weighing myself three time—one bad weight, then two good ones—but on the day of the argument I must have weighed myself ten or fifteen times; the weight just kept jumping around over a three-pound range, never landing on the same number twice in a row.
That night I took the scale apart and was a little surprised at what I saw. Traditional dial-type scales1 use a system of levers to collect the weight from the platform and transmit it to a single spring that controls the dial. You can see an example in this How Stuff Works article. I was expecting the same thing, but with the spring and dial replaced by a load cell and an LCD screen. What I found instead was four load cells and no lever mechanism whatsoever.

There was a load cell (and we’ll get to what a load cell is in a minute) mounted in the top half of the scale above each foot. You can see two of the four load cells in the photo. I couldn’t show all the load cells in a single photo because the top and bottom halves of the scale were connected by short wires that I didn’t want to disconnect.
The scales round rubber feet are actually the bottoms of plungers that push up into the load cells. Each load cell senses the force acting on it and sends a signal to the central circuit board, which adds the four values and displays the result on the LCD.
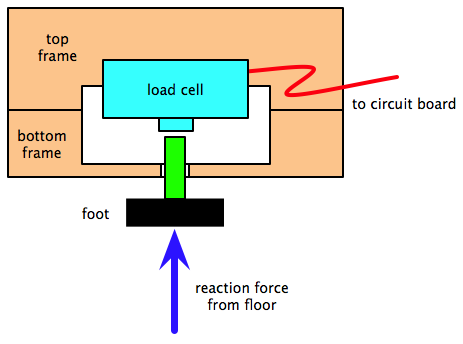
Presumably, Conair made the scale this way because they wanted a low-profile scale and didn’t have room for the usual lever mechanism.
So what’s a load cell? A load cell is a device that, through its deflection, tells us the force that’s acting on it. Load cells come in many shapes and sizes, but they all rely on Hooke’s Law.
Robert Hooke was a brilliant 17th century English scientist/engineer/architect whose name is not as well known as it should be because:
- He was a contemporary of Isaac Newton’s, and anyone working at the same time as Newton is likely to be overshadowed.
- He got on Newton’s bad side, which was not the right side to be on, as Gottfried Leibnitz and William Chaloner could attest. Hooke claimed that some of Newton’s work in gravitation was derivative of his own, an affront Newton never forgave, even after Hooke’s death in 1703. When Newton supervised the Royal Society’s move from Gresham College in 1705, Hooke’s portrait and some of his experimental instruments were conveniently lost.
Still, Hooke’s name is well known among engineers because of his law of linear elasticity, a cornerstone of much civil and mechanical engineering analysis. Amazingly, Hooke first published his law as an anagram. It wasn’t until a few years later that he published a proper paper on the subject, “De Potentia Restitutiva, or Of Spring.”

Here’s his explanation of the anagram:

About two years since I printed this Theory in an Anagram at the end of my Book of the Descriptions of Helioscopes, viz. c e i i i n o s s s t t u v, id est, Ut tensio sic vis; That is, The Power of any Spring is in the same proportion with the Tension thereof: That is, if one power stretch or bend it one space, two will bend it two, and three will bend it three, and so forward. Now as the Theory is very short, so the way of trying it is very easie.
The usual translation of Ut tensio sic vis is As the extension, so the force: there is a linear relationship between force and deflection. In mathematical terms, Hooke’s Law is typically written like this,
where is the force, is the deflection, and is the constant of proportionality, usually called the spring constant.
“Of Spring” goes on to give several examples of springy things and describes experiments that prove the linear relationship. His claim to universality comes in this paragraph:

From all which it is very evident that the Rule or Law of Nature in every springing body is, that the force or power thereof to restore it self to its natural position is always proportionate to the Distance or space it is removed therefrom, whether, it be by rarefaction, or separation of its parts the one from the other, or by a Condensation, or crowding of those, parts nearer together. Nor is it observable in these bodys only, but in all other springy bodies whatsoever, whether Metal, Wood, Stones, baked Earths, Hair, Horns, Silk, Bones, Sinews, Glass, and the like. Respect being had to the particular figures of the bodies bended, and the advantagious or disadvantagious ways of bending them.
You could make a very good argument that this paragraph is just bullshit. Of these materials, only Glass and baked Earths (assuming by the latter he means ceramics) follow Hooke’s Law reasonably well up to their breaking point. The others exhibit distinctly non-Hookean behavior over some range of loading. They either don’t spring back to their original position (metals stressed above their yield point) or aren’t linear in their elasticity (sinews).
Hooke must have known this. One of his prime examples is the coiled spring, made by bending a metal wire into a helix. While the finished spring certainly follows Hooke’s Law up to some load, the wire itself just as certainly didn’t follow Hooke’s Law as it was being bent into the coiled form in the first place—if it had, it would have sprung back to being a straight wire.
What was important to Hooke, and what is still important to us, is that many materials are linearly elastic over the range of loading they are typically subjected to in the finished product. Yes, you can bend a piece of wood beyond the linear range, but you don’t build a house out of wood stressed that highly. The wood joists in the floor below me are bending slightly under my weight, but they will spring back when I leave the room. Most manmade structures and devices are built to be used within the linearly elastic range, and that’s why Hooke’s Law works.
So, back to load cells. The simplest load cell is an old-fashioned spring fish scale. Here’s a handsome example whose photo I nicked from Malolo Blue Water Tackle.

The pointer moves along the body as the coiled spring inside deflects under the weight of the fish. The weight markings are uniformly spaced because of Hooke’s Law: As the extension, so the force.
But Hooke’s Law tells us that we don’t need to used coiled springs to measure force. Any structure that isn’t overstressed will display a linear relationship between force and deflection; we just have to be able to measure that deflection. Most structures don’t deflect visibly when lightly loaded, but we can still measure their deflection by drawing on a little knowledge from electrical engineering.
When a conductor is stretched and made thinner, or compressed and made fatter, its resistance changes linearly with the strain2. By laying out a thin wire or foil in a serpentine (for increased sensitivity) and bonding it to a structure, we can monitor the deformation at that point in the structure by keeping track of the resistance. This wire or foil serpentine is known as a strain gauge. Here’s a drawing of a strain gauge from Wikipedia.
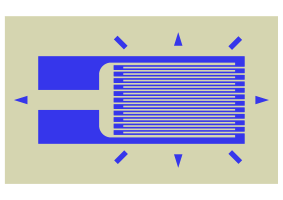
By attaching one or more strain gauges to a structure, we create a load cell. The linearity between resistance and strain, combined with the linearity between strain and force, gives the load cell a linear relationship between resistance and force, which is very convenient. A simple multiplication of the resistance converts it into a force.
I wanted to show you a nice closeup photo of a load cell from my bathroom scale, but I was afraid that pulling one out would ruin it. So instead I photographed the load cell in a ten-pound force gauge (a sort of handheld scale) I use quite often in my regular work. I’ve had this gauge apart several times to change the battery, so I knew the load cell in it was easily visible.
Here’s the force gauge itself. The force being measured is applied through the little threaded stub coming out of the top. I screw a hook onto that stub to measure tensile loads and a flat button to measure compressive loads. The loads appear on the now-blank LCD screen.

If we open it up, we see the load cell connected to the stub and the circuit board that does the calculating and runs the LCD. The battery that powers the device is hidden behind the blue foam.

This load cell has four strain gauges bonded to it near the semicircular cutouts.

Four strain gauges are used instead of just one to filter out side loading of the stub. The purpose of the gauge is to measure only forces directed along the stub.
The load cells in my bathroom scale aren’t going to be as robust as the one in the force gauge, but the idea is the same: When I stand on the scale, my weight creates strain in the load cell according to Hooke’s Law. That strain is converted to an electrical signal that’s interpreted by some circuitry and displayed as a force on the scale’s LCD.
That’s the theory; what about practice? Why was my scale giving different results every time I stepped on it? I’m pretty sure there was some obstruction in one or more of the plungers, which was affecting the load transmitted to the load cells. I never found an obstruction, but when I had the scale apart I blew air in and around the plungers and exercised them several times to make sure they all moved freely. Since then, the scale has worked perfectly. Now I step on the scale only twice each morning because I get the same result each time.
-
I’ve noticed people calling these “analog scales,” apparently unaware that for something to be analog, there must be an analogy. I guess analog now means “not digital.” ↩
-
I don’t want to get into the formal definition of strain; this post is already too long. Suffice it to say that strain is a measure of deformation, like the in Hooke’s Law. ↩

