Now we see the violence inherent in Hooke’s Law
May 18, 2013 at 10:31 AM by Dr. Drang
This is the post where I explain how I avoided shooting my older son with the head of a screw. Two heads of screws, actually, but we’ll get into the details later. The underlying topic is strain energy, its potential1 for harm, and the respect it should be paid.
As I said a few days ago, the inspiration for this post—apart from the actual incident in which I avoided shooting my son—was this episode of Gabe Weatherhead and Erik Hess’s Generational podcast, in which they talked about the dangers of their respective former professions—Gabe as a research chemist and Erik as a fighter pilot. The dangers associated with being a fighter pilot are pretty obvious; those associated with being a research chemist are probably less obvious, but you can get a good sense of them from the title of the episode: “What Happened When Gabe Set Himself on Fire.”
Like chemistry labs, mechanical testing labs have their own set of dangers, most of which involve the sudden, unexpected release of strain energy. You learned about strain energy in high school physics, although your teacher probably didn’t call it that. Shortly after learning about the forces in springs and Hooke’s Law, (a topic we’ve looked at here once or twice), you learned that the potential energy2 stored in a spring is expressed by this formula:
The in the formula is the spring constant, which is a measure of how stiff the spring is. It’s measured in units like pounds per inch or newtons per millimeter—force per length—and is always a positive value. The is the amount, as measured in inches or millimeters or some other unit of length, the spring has stretched from its natural, unloaded length. The sign convention for is arbitrary, but it’s usually taken that positive values of represent lengthening of the spring and negative values represent shortening.
You see, then, that because is squared, the potential energy in the spring is either zero (when the spring is at its natural length) or positive. This makes sense because potential energy is defined as the ability to do work. A compressed spring is able to do just as much work as a stretched spring, so their potential energies should be the same and should have the same sign. And a spring that’s neither stretched nor compressed can’t do any work, so its potential energy should be zero. So far, so good.
The reason Hooke’s Law works on a macro scale for things like coiled springs is that a very similar sort of law works on a micro scale within the spring wire. On the micro scale, the force-displacement relationship, , is replaced by a similar relationship between stresses (which are like forces) and strains (which are derived from deformations). In the same way that the potential energy stored in a spring is a function of its stretch, the potential energy in any deformed body is a function of its strain. Hence the term “strain energy.”
The details I’ve glossed over in the previous paragraph would fill, and do fill, volumes. My shoulders are sore from all the hand-waving, but I’ll push on.
When it comes to the ability to do harm, not all strains are created equal. It’s only the elastic strains—those which can be reversed when the load is removed—that present a danger. If you stretch a rubber band in front of your face and let go, it’ll snap back and hit you in the nose. That won’t happen if you do the same thing with a ring of Play-Doh. In a mechanical testing lab, we’re usually applying very large forces to parts and materials that have a lot of reversable elastic strain. And when things break, whether intentionally or unintentionally, the huge strain energy that’s built up as the parts have been loaded is suddenly released and turned into kinetic energy. Lab safety is all about directing that kinetic energy to where it won’t hurt anyone.
Which brings us, finally, to my son and the screw heads. One weekend a few months ago he was helping me finish up a few tests. The tests were intended to break things, and I had barriers set up to block any pieces that might come flying out at us. And of course we were wearing goggles. The tests went smoothly and no one came close to getting hurt.
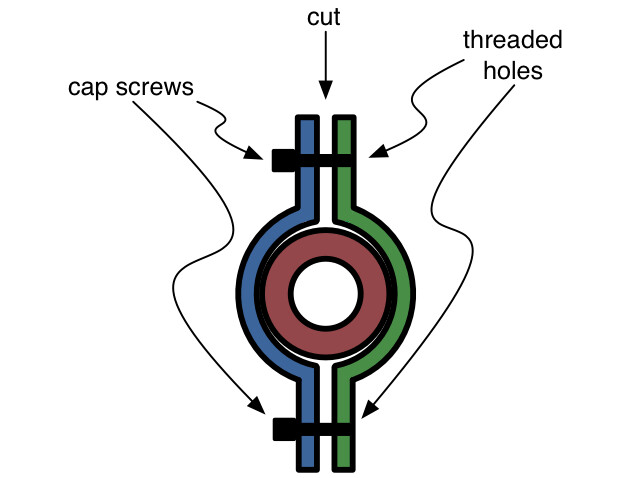
We ran into a snag while taking the equipment apart. One of the pieces of the test fixture was a pipe clamped in place by four capscrews like this one:
Source: littlemachineshop.com
A side view of the clamping arrangement looked like this, with two screws on the top and two on the bottom (you see only one in each position because its mate is behind it). The screws passed through unthreaded holes in the blue piece and screwed into threaded holes in the green piece.
I had clamped and loosened this pipe many times over the previous month of testing, and internal hex surfaces of the capscrews had rounded out. Finally, after the testing was over, the Allen wrench wouldn’t grip in the screwheads and I couldn’t loosen the clamp and remove the pipe.
So I grabbed a hacksaw, slid its blade down the gap between the blue and green pieces, and drew it back to start cutting. That’s when I noticed my son standing to the left, directly in line with the screw heads.
Let me digress at this moment of high tension3 and explain how bolts and screws work. Most people know that bolted joints4 require sufficient torque to do their job. Many of you have probably used a torque wrench at one time or another. But most people don’t realize that torque, in and of itself, is meaningless. Bolted joints work because of the tension in the bolts, not the torque. The purpose of applying torque to a bolt is to use the mechanical advantage of the thread (which is essentially an inclined plane wrapped around in a helix) to stretch the bolt and induce tension in it. There are, in fact, bolting systems in which a hydraulic machine stretches a bolt directly by pulling on its tail and then spins the nut up tight to maintain that stretch—no torque of any significance is ever applied.
The word “stretch” in the previous paragraph should prick up you ears. Strain energy is stored in every fully tightened bolt because that bolt has been stretched. When such a bolt breaks or is cut, that strain energy gets released somehow, often by sending the bolt head flying.
In this case, there’s even more strain energy available. The flanges on the two clamp pieces are bent under the load of the screws. When the screws are cut, they’ll straighten back out, acting as a catapult to fling the screw heads.
“You need to move around to the other side,” I said.
“Why?”
“Because when I cut through, these screws are going to shoot out like bullets, and you’re standing in the way.”
“Really?” I should mention that my son is sixteen years old and therefore assumes that I’m full of shit. But he moved anyway.
I did a suprisingly good job of cutting evenly through the two top screws, and they snapped almost simultaneously. The screw heads shot across the lab and hit a piece of plywood leaning against the opposite wall with a loud th-thunk. I was vindicated; when I had to cut another recalcitrant screw a few minutes later, he stayed well out of the line of fire.
While I was happy to have proved myself not entirely full of shit, I was annoyed at my brief lapse. I’d been careful during the test but let my guard down briefly during disassembly. I should never have even picked up the hacksaw before clearing him out of the way. Strain energy is not to be messed with.
-
You may not get that joke yet, but Ben Deaton is laughing his ass off right now. ↩
-
Yes, that was the joke. ↩
-
I slay me. ↩
-
There is a technical difference between bolts and screws, but it has nothing to do with this discussion, so I’m going to use the words interchangably from now on. ↩