A simple PCalc specialty calculator
September 26, 2014 at 10:34 PM by Dr. Drang
Last week, in my post about PCalc 3.3, I said
with a little thought and a little programming, you could turn PCalc into a whole series of special-purpose calculators.
Here’s an example that took very little thought.
Tip calculators have been a heavily populated subgenre of the App Store for as long as there’s been App Store. The idea behind all of them is to present a clean interface that makes it easy to enter the amount of the check and quickly return the tip and the total. I decided to try my hand at doing the same thing within PCalc.
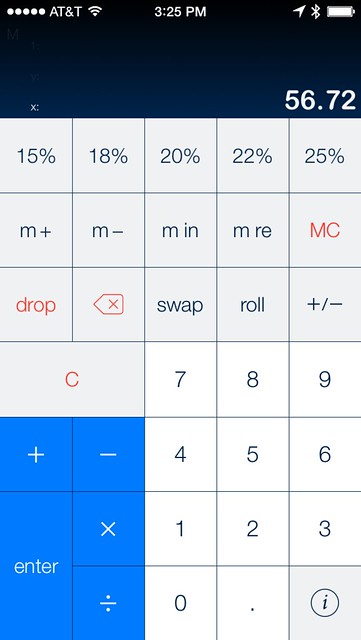
The layout has more than just digit entry, because I figured you sometimes need to do some elementary math. But in the most common case, you enter the amount of the check
and then tap one of the percentage buttons along the top. For 20%, the result is this:
The y-register has the amount of the tip and the x-register has the total. The total has been rounded: rounded down if it’s less than 10¢ above a whole-dollar about and rounded up otherwise. If I had PCalc’s display mode set to Accounting, both values would have two digits after the decimal point, but since I don’t use Accounting mode normally, I haven’t set it here.
What I like about this result is that the two numbers are in the order you typically see on a credit card receipt.
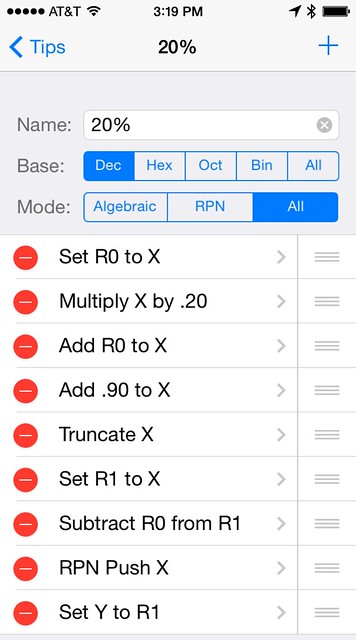
The calculation is done through a user-defined function:
There are similar functions for the other tip percentages. The rounding is done in the and lines.
You’ve no doubt noticed that I’ve shown the layout in RPN mode. Unfortunately, this isn’t just because I prefer RPN. See the command in the second to last line? At present, that’s the only way PCalc can put a value into the y-register if there isn’t one already there. And because is only available in RPN mode, I couldn’t write a function that worked the way I wanted in Algebraic mode. That’s fine for Drang, but it might not be fine for you.1
But if RPN is your thing, and you want to use or modify this specialty calculator, you can download the layout and the set of functions.
Update 9/27/14
The two preceding paragraphs are sort of correct but horribly misleading. This tweet from Josh Asch gets to the heart of the matter:
@drdrang Not sure what you mean about “if there isn’t already a value in Y”, because AC sets to 0. This works for me:
— Josh Asch (@jobbogamer) Sep 27 2014 4:52 AM
Josh’s version of the script—which is the same as mine but with the second-to-last line deleted—works when you’re using Algebraic mode but fails in RPN mode. My original script works in RPN but fails in Algebraic.
What I said originally about not working unless there’s a value already in the y-register is true only for RPN. So if you’re an Algebraic user, you can install my Tips functions and delete the penultimate line from each. I’ve also updated the Tips layout to have buttons appropriate for both modes. Unless you change your settings to show the y-register in the second line (I suspect most Algebraic users don’t), you’ll need to use the key to flip between the tip and total values.
And I don’t think there’s any need to be coy: The next point release of PCalc will allow to work in RPN. When it’s released, Josh’s versions of the Tips functions (which is how I had wanted to write them in the first place) will work in both modes.
Update 10/4/14
Version 3.3.1 of PCalc has smoothed over the differences between the y-register behavior in RPN and algebraic modes. The downloadable functions and layouts described above now work in both modes. For more information, and screenshots, see this more recent post.
One last thing. If you have Launch Center Pro, or use some other utility that understands URL schemes, you can launch PCalc directly into the Tips layout via this URL:
pcalc://vlayout/tips
That’s what’s triggered by the lower left button in my LCP setup.
The “regular” PCalc button in the bottom center position launches PCalc in my usual layout:
pcalc://vlayout/drang
-
I have reason to believe a future version of PCalc will allow setting the y-register in Algebraic mode. ↩