SciPy and image analysis
September 16, 2014 at 8:34 PM by Dr. Drang
“Image analysis” is a little too hifalutin for what I did today, but it was fun and I solved a real problem.
I had a scanned drawing of the cross section of a hollow extruded aluminum part and needed to calculate the enclosed volume. Because the part’s exterior and interior surfaces were curved—and not arcs of circles or ellipses—straightforward area calculations weren’t possible. But I figured I could make a good estimate by counting pixels and scaling.
The drawing looked sort of like this, only more complicated. There were internal partition walls and more dimension lines.
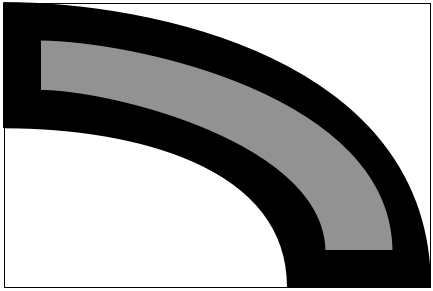
I opened the scan in Acorn, erased the dimension lines, and filled the solid parts with black and the hollows with 50% gray. Then I cropped it down to the smallest enclosing rectangle, the (physical) dimensions of which were given on the drawing. I ended up with something like this:
The image I had was dirtier than this because there were antialiasing artifacts from the scanning process, but you get the idea.
I had hopes that I could get the count of gray pixels directly from a histogram in Acorn, but I couldn’t find a command that would do that, so I shifted to Python.
The misc sublibrary of SciPy has an imread function that was just what I needed. It reads an image file (PNG, TIFF, JPEG) and turns it into a NumPy array of RGBA or gray values. With that array in hand, I could just scan through it, count the pixels that are at or near 50% gray, and calculate their percentage of the total. Here’s the script:
python:
1: #!/usr/bin/python
2:
3: from scipy import misc
4: import sys
5:
6: img = misc.imread(sys.argv[1], flatten=True)
7: white = gray = black = 0
8: lower = 255/3
9: upper = 2*lower
10: height, width = img.shape
11:
12: for i in range(height):
13: for j in range(width):
14: if img[i,j] >= lower:
15: if img[i,j] <= upper:
16: gray += 1
17: else:
18: white += 1
19: else:
20: black += 1
21:
22: all = width*height
23: print "Total pixels: %d" % all
24: print "White pixels: %d (%5.2f%%)" % (white, 100.0*white/all)
25: print "Black pixels: %d (%5.2f%%)" % (black, 100.0*black/all)
26: print "Gray pixels: %d (%5.2f%%)" % (gray, 100.0*gray/all)
I did a bit more than was needed, counting the white and black pixels as well as the gray.
Line 6 does the hard work—reading in the file, converting it to grayscale (with flatten=True), and putting it into an array. The tonal range of 255 was split in thirds in Lines 8 and 9 and every pixel within each third was lumped together. If I’d chosen different values for lower and upper, I would’ve gotten different results, but not too much different. The great majority of pixels had values of either 0, 128, or 255; only the antialiasing pixels at the edges of the lines were different.
The results looked like this:
Total pixels: 126003
White pixels: 63342 (50.27%)
Black pixels: 39870 (31.64%)
Gray pixels: 22791 (18.09%)
Multiplying the percentage of grays by the physical height and width of the enclosing rectangle gave me the cross-sectional area of the hollow. Multiplying that by the length of the extrusion gave me the volume. Two significant digits was all I really needed in the result, which is why I didn’t stress over the antialiasing pixels.
There are, I know, commercial programs that can do this and more. But most of them run on Windows (because most engineers use Windows), and the time I would’ve spent finding one and learning how to use it couldn’t have been too much less than the time it took to write 26 lines of code. And I know exactly how this code works.
Update 9/17/14
Alexandre Chabot rewrote my script to get rid of the loops in Lines 12–21 and replace them with NumPy’s sum function and a set of array-based Boolean expressions. For example,
python:
white = np.sum(img > upper)
returns the count of all the white pixels. The expression in the argument, img > upper compares each item in img to upper and returns an array of Trues and Falses. When that’s fed to sum, it returns the sum of all the Trues. Very nice.
Treating arrays in chunks like this is how NumPy is supposed to be used. I used loops because that’s what I’ve been doing for 35 years and old habits are hard to break.