Next post Previous post

Slippin’ and a-slidin’

March 14, 2015 at 1:49 AM by Dr. Drang

Tuesday night I was sitting in a hotel room up in God’s Country,1 getting ready for a meeting the following day, when my phone dinged. It was an email from Glenn Fleishman, who was working on this article about the USB-C connection on the new MacBook and how it wasn’t going to be as trip-proof or snag-proof as the MagSafe power connection it was replacing. He was asking several people for their thoughts, opinions, and calculations and wanted to throw mine into the mix. It seemed like more fun than preparing for a meeting, so I sent him a short analysis. I assumed the details of the analysis wouldn’t be appropriate for a Macworld article, so I asked if I could go over them here after his article was published. He said yes, and that’s why we’re gathered here today.

I assume you read Glenn’s article yesterday. It got a lot of links and praise in the Mac corner of the internet, and deservedly so. It’s an exploration of a question that should worry those who plan to buy one of the new MacBooks: Given how light the computer is and how tight the USB-C connection is, are we returning to the days when tripping over a computer’s power cable meant a crash to the floor?

There are, of course, an infinite number of orientations and angles at which the cable can be pulled, so Glenn wisely decided to cut through the complexity and look at the most straightforward arrangement: a horizontal pull on the cable directly out from the side of the MacBook. Even with this simplification, there are two problems that have to be solved.

Glenn had already solved the first one, which is determining whether the friction within the USB-C connection was sufficient to allow the MacBook to be dragged along the table by pulling on the cable. As a first step, he had looked up the extraction force in the USB-C spec and found this:

The connector extraction force shall be within the range of 8 N to 20 N before and after the specified insertion/extraction or durability cycles.

In case it’s been a while since your last physics class, the “N” in that paragraph refers to newtons, the standard SI unit of force. One newton is a little under a quarter of a pound. My favorite way of remembering this is that a newton is roughly the weight of a small apple.

The next step is to determine the MacBook’s resistance to sliding. That’s going to be the product of the normal force between the table and the computer—which is the MacBook’s weight, 9 N—and the coefficient of friction between the computer’s rubber feet and the table. Glenn used a handbook value of 0.7 for the rubber-on-wood coefficient of friction, a number I thought was an overestimate based on my experience with my MacBook Air. I ran a couple of tests there in the hotel room and got a value closer to 0.4. In the article, Glenn politely used both values, but here I’m going to stick to 0.4. Because we don’t have a new MacBook to test, neither of us really knows.

(Glenn mentioned another wrinkle pointed out to him by Bradley Grzesiak: a 1942 study from the National Bureau of Standards that showed the coefficient of friction of rubber against various surfaces can vary wildly with sliding speed. In this first analysis, we’re looking at static friction only, so sliding speed doesn’t enter into the problem. But we will be looking into sliding later. Even so, I’m not sure how applicable this study is to our situation. It was concerned with soft rubber, and the feet on my MacBook Air are anything but soft. In fact, I’ve often wished they were soft so they’d be stickier. Again, until we know more about the new MacBook, we’re just making estimates.)

So the resistance to sliding is 0.4×9N=3.6N0.4\times9\;\mathrm{N} = 3.6\;\mathrm{N}, which is well below the minimum extraction force of 8N8\;\mathrm{N}. So it’s pretty clear that you will be able to drag your new MacBook across a table by pulling on the power cord.

But there’s more to the problem than that. If the MacBook starts accelerating during the pull, then its own inertia will create another resistive force to be added to the friction. If the cable is jerked fast enough, the MacBook will move a bit, but the connector will come out before it moves much. In principle, this is like the trick of yanking a tablecloth out from under a table full of dishes.

It’s this dynamic problem that I analyzed Tuesday night and sent to Glenn. Here’s the solution I wrote out in my notebook:

MacBook pull

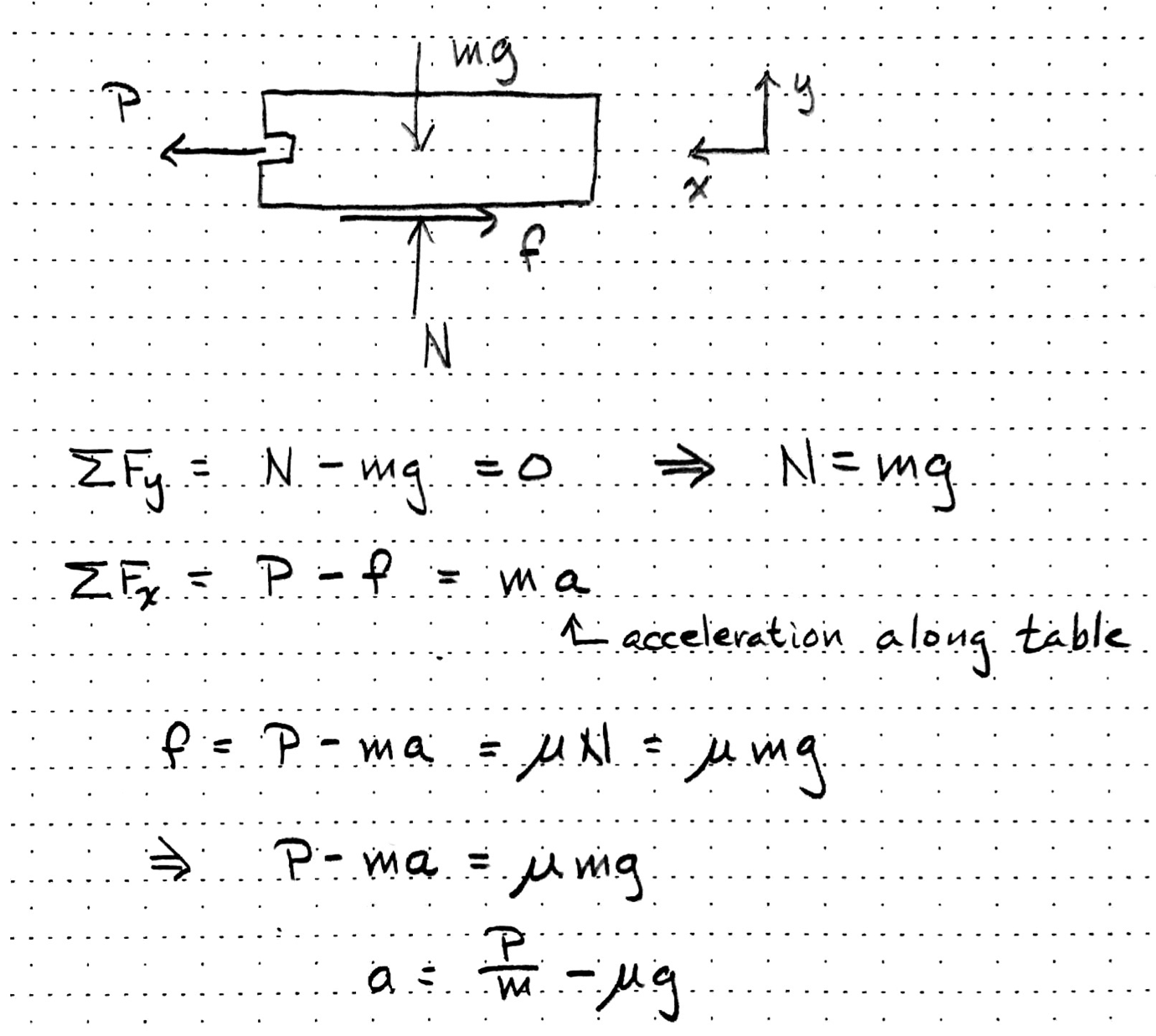
The drawing at the top is a free-body diagram of the MacBook, looking a lot chunkier than Jony Ive would like. The forces acting on it are: PP, the extraction force of the connector; mgmg, the weight (mass time acceleration due to gravity) of the MacBook; NN, the normal force2 exerted by the table on the MacBook, and ff, the friction force exerted by the table on the (sliding) MacBook.3

Because there’s no acceleration in the vertical direction, the normal force is equal to the weight. And because the MacBook is sliding, the friction force is equal to the product of the normal force and the coefficient of friction:

f=μN=μmgf = \mu N = \mu m g

Using this and Newton’s 2nd Law in the horizontal direction leads us to the final equation,

a=Pm−μga = \frac{P}{m} - \mu g

What does this tell us? If we plug in the values for all the terms on the right, it’ll give us the acceleration of the MacBook as we pull the USB-C plug out. It is, therefore, the smallest acceleration of the cord for which the connector will come out.

We can calculate this acceleration for both the minimum and maximum extraction forces allowed by the USB-C spec:4

a=8N0.92kg−0.4(9.81m/s2)=4.8m/s2a = \frac{8\;\mathrm{N}}{0.92\;\mathrm{kg}} - 0.4(9.81\;\mathrm{m/s^2}) = 4.8\;\mathrm{m/s^2} a=20N0.92kg−0.4(9.81m/s2)=17.8m/s2a = \frac{20\;\mathrm{N}}{0.92\;\mathrm{kg}} - 0.4(9.81\;\mathrm{m/s^2}) = 17.8\;\mathrm{m/s^2}

So you can yank out a connector at the loose end of the range with a cord acceleration greater than 4.8m/s24.8\;\mathrm{m/s^2}, but one at the tight end of the range will take 17.8m/s217.8\;\mathrm{m/s^2}. That’s where those numbers came from in Glenn’s article.

Now let’s figure out how far will the MacBook move as we yank the cord out. As an example we’ll assume the cord is being pulled at a 1g1\;\mathrm{g} (9.81m/s29.81\;\mathrm{m/s^2}) acceleration and we have the loosest allowable USB-C connection. Therefore, the plug at the end of the cord, which is 6 mm long according to the spec, is moving at 5m/s25\;\mathrm{m/s^2} relative to the MacBook. It will take

t=2(0.006m)5m/s2=0.049st = \sqrt{\frac{2 (0.006\;\mathrm{m})}{5\;\mathrm{m/s^2}}} = 0.049\;\mathrm{s}

for the plug to pull out, during which time the MacBook will have moved

d=12(4.8m/ss)(0.049s)2=0.0058md = \frac{1}{2} (4.8\;\mathrm{m/s^s})(0.049\;\mathrm{s})^2 = 0.0058\;\mathrm{m}

or about 6 mm. Is it a coincidence that this is about the same as the length of the plug? Sort of. It’s because I chose for this example a cord acceleration roughly twice that of the MacBook. Had I chosen a lower cord acceleration, the MacBook would move more; had I chosen a higher cord acceleration, the MacBook would move less.

We’re not actually done, though. When the plug pulls out, the MacBook is moving at a velocity of

v=(4.8m/ss)(0.049s)=0.235m/sv = (4.8\;\mathrm{m/s^s})(0.049\;\mathrm{s}) = 0.235\;\mathrm{m/s}

It now has to decelerate to a stop. With a frictional force of 3.6N3.6\;\mathrm{N} acting to slow it down, it will decelerate at a rate of

ad=fm=3.6N0.92kg=3.9m/s2a_d = \frac{f}{m} = \frac{3.6\;\mathrm{N}}{0.92\;\mathrm{kg}} = 3.9\;\mathrm{m/s^2}

and will come to a stop in another

dd=v22ad=(0.235m/s)22(3.9m/s2)=0.007md_d = \frac{v^2}{2 a_d} = \frac{(0.235\;\mathrm{m/s})^2}{2 (3.9\;\mathrm{m/s^2})} = 0.007\;\mathrm{m}

or 7 mm. That means it moved a total of about 13 mm. Half an inch. Not bad, but remember we’re assuming

  1. A straight pull out the side of the MacBook.
  2. A pretty decent yank on the cord.
  3. The loosest possible connector.

We’re not likely to get that combination in the real world. Most cord entanglements are slow motion disasters, where you immediately feel yourself getting caught but just can’t stop in time. And the pull is almost never straight out. Glenn is right to be pessimistic.

But let’s not end on a downer. You didn’t think I chose the title of the post at random, did you?

Jimmy Iovine is listed as engineer on the album, but its recording history is so fragmented, I’m not sure he worked on this track. But let’s say he did just to make a stronger connection to Apple.

  1. Also known as the home of kraeusening, the most natural way to brew beer. And the most expensive. ↩

  2. “Normal” in this situation has the mathematical meaning of “at right angles to a surface.” It doesn’t mean “ordinary.” ↩

  3. Two reasons why I’m not accounting for the possibility of horizontal rotation as the cord is being pulled:

    1. When the lid of my MacBook Air is up, the center of gravity of the computer is reasonably well aligned with the power plug.
    2. I have no idea where the c.g. of the new MacBook is, so any attempt to handle horizontal rotation would be a lot of work with very little justification.

    ↩

  4. Yes, I’m pushing the significant digits further than I should. ↩

Next post Previous post