Amazing calendar
January 1, 2018 at 10:12 AM by Dr. Drang
Knowing my interest in calendrical idiocy, longtime friend of the blog Allen MacKenzie tweeted me about a meme running around on Twitter and Facebook during the second half of December. You’ll see it if you search on “amazing calendar 2018 sunday.”
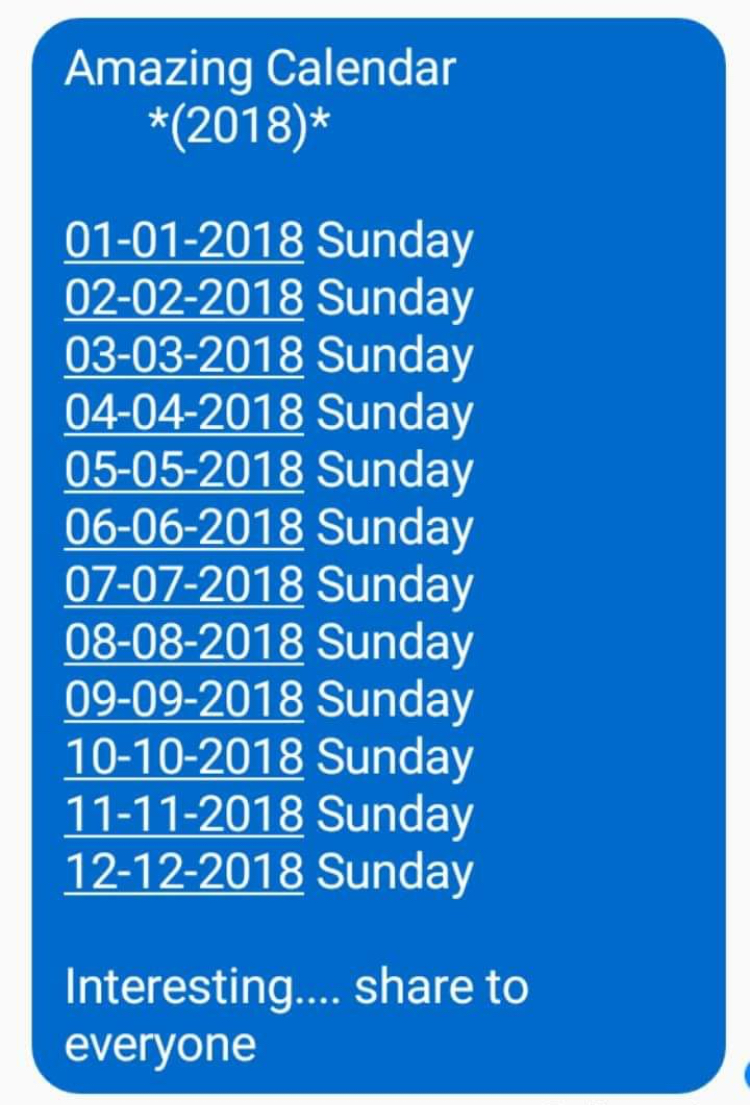
Offhand, I can think of three reasons to disbelieve this without even looking at a 2018 calendar:
- For an advance of one month and one day to end up on the same day of the week, the length of a month would have to be one less than a multiple of seven. There are no months with 27 or 34 days.
- If this happens in 2018, it would have to happen in every other nonleap year (albeit with a different day being repeated). Surely we would have heard about it if all those same days in 2017 fell on a Saturday.
- January 1, 2018 is a Monday, not a Sunday! Getting the first one wrong kind of throws the whole series into doubt.
OK, so it’s obvious that these dates don’t all fall on the same day of the week. But I wondered if all seven days of the week were covered by these dates. There are twelve of them, but repetitions could leave some days of the week unused.1
I could, of course, just look at a calendar or issue the cal command, but where’s the fun in that? I decided to solve the problem with a short Python script:
python:
1: #!/usr/bin/env python
2:
3: from datetime import date
4:
5: common = [ date(2018, m, m) for m in range(1, 13) ]
6: common_doy = [ int(x.strftime('%j')) for x in common ]
7: common_dow = [ (x - common_doy[0]) % 7 for x in common_doy ]
8: leap = [ date(2020, m, m) for m in range(1, 13) ]
9: leap_doy = [ int(x.strftime('%j')) for x in leap ]
10: leap_dow = [ (x - leap_doy[0]) % 7 for x in leap_doy ]
11:
12: print(" Day of week")
13: print("Month Common Leap")
14: for m in range(12):
15: print(" {} {} {}".format(common[m].strftime('%b'), common_dow[m], leap_dow[m]))
16:
17: wdays = set(range(7))
18: common_missing = wdays - set(common_dow)
19: leap_missing = wdays - set(leap_dow)
20: if common_missing:
21: print("\nMissing from common year: {}".format(tuple(common_missing)))
22: else:
23: print("\nMissing from common year: None")
24:
25: if leap_missing:
26: print("Missing from leap year: {}".format(tuple(leap_missing)))
27: else:
28: print("Missing from leap year: None")
Lines 5 and 8 generate the “amazing” dates for a common year and a leap year. These are dates where the month and day numbers are the same. I chose 2018 for the common year and 2020 for the leap year, but any such years would do. Lines 6 and 9 use the %j code for strftime to get the day-of-year number for each of the days of interest. Lines 7 and 10 then do some modular arithmetic to calculate a generic day-of-week number. This is a number that runs from 0 to 6 and starts at zero on the first day of interest. I could have used the datetime module’s weekday function, but that would have made the common_dow and leap_dow lists specific to the years 2018 and 2020, and I wanted a more general solution.
Lines 12–15 print out a table of results, which we’ll see in a bit. Lines 17–19 figure out which, if any, days of the week are missing from the days of interest using set differences. The common_missing and leap_missing sets are then used in Lines 20–28 to determine what gets printed out in the summary after the table.
(Note that all the prints in this program are function calls. Yes, I’ve finally moved to Python 3 for all new scripts, and I don’t expect to post any more Python 2 stuff here.)
Here’s the output. Days of the week are numbered from 0 through 6, starting on 1/1.
Day of week
Month Common Leap
Jan 0 0
Feb 4 4
Mar 5 6
Apr 2 3
May 5 6
Jun 2 3
Jul 5 6
Aug 2 3
Sep 6 0
Oct 2 3
Nov 6 0
Dec 2 3
Missing from common year: (1, 3)
Missing from leap year: (1, 2, 5)
So we see that not every day of the week is covered by these doubled dates. This year, where 1/1 is a Monday, there are no doubled dates on a Tuesday or Thursday. Next year, there will be no doubled dates on a Wednesday or Friday. In 2020, there will be no doubled dates on Thursday, Friday, or Monday. And so on.
What about the first of every month? Just change Lines 5 and 8 to
python:
5: common = [ date(2018, m, 1) for m in range(1, 13) ]
8: leap = [ date(2020, m, 1) for m in range(1, 13) ]
and the output will be
Day of week
Month Common Leap
Jan 0 0
Feb 3 3
Mar 3 4
Apr 6 0
May 1 2
Jun 4 5
Jul 6 0
Aug 2 3
Sep 5 6
Oct 0 1
Nov 3 4
Dec 5 6
Missing from common year: None
Missing from leap year: None
Firsts of the month cover all the days of the week in both common and leap years. This isn’t the most momentous issue in the world, but let’s start the year off gently.
-
One nice thing about these dates is they’re unambiguous. They represent the same day whether you’re using DMY or MDY format, so I won’t hear from a lot of snippy Europeans telling me I’m doing dates wrong. ↩

