Python module for section properties
January 15, 2018 at 9:34 PM by Dr. Drang
A lot of what I do at work involves analyzing the bending of beams, and that means using properties of the beams’ cross sections. The properties of greatest importance are the area, the location of the centroid, and the moments of inertia. Most of the time, I can just look these properties up in a handbook, as I did in this post, or combine the properties of a few well-known shapes. Recently, though, I needed the section properties of an oddball shape, and my handbooks failed me.
In the past, I would open a commercial program that had a section properties module, draw in the shape, and copy out the results. But my partners and I stopped paying the license for that program several years ago, so that wasn’t an option anymore. I decided to write a Python module to do the calculations and draw the cross-section.
If the cross section is a polygon, there are formulas for calculating the section properties from the coordinates of the vertices. Most of the formulas are on the aforelinked Wikipedia pages and on this very nice page from Paul Bourke of the University of Western Australia. I’ll explain how and why the formulas work in a later post; for now, we’ll just accept them. For cross sections that aren’t polygons, we can create a close approximation by fitting a series of short straight lines to any boundary curve.
Here’s the source code of the module, which I call section.py:
python:
1: import matplotlib.pyplot as plt
2: from math import atan2, sin, cos, sqrt, pi, degrees
3:
4: def area(pts):
5: 'Area of cross-section.'
6:
7: if pts[0] != pts[-1]:
8: pts = pts + pts[:1]
9: x = [ c[0] for c in pts ]
10: y = [ c[1] for c in pts ]
11: s = 0
12: for i in range(len(pts) - 1):
13: s += x[i]*y[i+1] - x[i+1]*y[i]
14: return s/2
15:
16:
17: def centroid(pts):
18: 'Location of centroid.'
19:
20: if pts[0] != pts[-1]:
21: pts = pts + pts[:1]
22: x = [ c[0] for c in pts ]
23: y = [ c[1] for c in pts ]
24: sx = sy = 0
25: a = area(pts)
26: for i in range(len(pts) - 1):
27: sx += (x[i] + x[i+1])*(x[i]*y[i+1] - x[i+1]*y[i])
28: sy += (y[i] + y[i+1])*(x[i]*y[i+1] - x[i+1]*y[i])
29: return sx/(6*a), sy/(6*a)
30:
31:
32: def inertia(pts):
33: 'Moments and product of inertia about centroid.'
34:
35: if pts[0] != pts[-1]:
36: pts = pts + pts[:1]
37: x = [ c[0] for c in pts ]
38: y = [ c[1] for c in pts ]
39: sxx = syy = sxy = 0
40: a = area(pts)
41: cx, cy = centroid(pts)
42: for i in range(len(pts) - 1):
43: sxx += (y[i]**2 + y[i]*y[i+1] + y[i+1]**2)*(x[i]*y[i+1] - x[i+1]*y[i])
44: syy += (x[i]**2 + x[i]*x[i+1] + x[i+1]**2)*(x[i]*y[i+1] - x[i+1]*y[i])
45: sxy += (x[i]*y[i+1] + 2*x[i]*y[i] + 2*x[i+1]*y[i+1] + x[i+1]*y[i])*(x[i]*y[i+1] - x[i+1]*y[i])
46: return sxx/12 - a*cy**2, syy/12 - a*cx**2, sxy/24 - a*cx*cy
47:
48:
49: def principal(Ixx, Iyy, Ixy):
50: 'Principal moments of inertia and orientation.'
51:
52: avg = (Ixx + Iyy)/2
53: diff = (Ixx - Iyy)/2 # signed
54: I1 = avg + sqrt(diff**2 + Ixy**2)
55: I2 = avg - sqrt(diff**2 + Ixy**2)
56: theta = atan2(-Ixy, diff)/2
57: return I1, I2, theta
58:
59:
60: def summary(pts):
61: 'Text summary of cross-sectional properties.'
62:
63: a = area(pts)
64: cx, cy = centroid(pts)
65: Ixx, Iyy, Ixy = inertia(pts)
66: I1, I2, theta = principal(Ixx, Iyy, Ixy)
67: summ = """Area
68: A = {}
69: Centroid
70: cx = {}
71: cy = {}
72: Moments and product of inertia
73: Ixx = {}
74: Iyy = {}
75: Ixy = {}
76: Principal moments of inertia and direction
77: I1 = {}
78: I2 = {}
79: θ︎ = {}°""".format(a, cx, cy, Ixx, Iyy, Ixy, I1, I2, degrees(theta))
80: return summ
81:
82:
83: def outline(pts, basename='section', format='pdf', size=(8, 8), dpi=100):
84: 'Draw an outline of the cross-section with centroid and principal axes.'
85:
86: if pts[0] != pts[-1]:
87: pts = pts + pts[:1]
88: x = [ c[0] for c in pts ]
89: y = [ c[1] for c in pts ]
90:
91: # Get the bounds of the cross-section
92: minx = min(x)
93: maxx = max(x)
94: miny = min(y)
95: maxy = max(y)
96:
97: # Whitespace border is 5% of the larger dimension
98: b = .05*max(maxx - minx, maxy - miny)
99:
100: # Get the properties needed for the centroid and principal axes
101: cx, cy = centroid(pts)
102: i = inertia(pts)
103: p = principal(*i)
104:
105: # Principal axes extend 10% of the minimum dimension from the centroid
106: length = min(maxx-minx, maxy-miny)/10
107: a1x = [cx - length*cos(p[2]), cx + length*cos(p[2])]
108: a1y = [cy - length*sin(p[2]), cy + length*sin(p[2])]
109: a2x = [cx - length*cos(p[2] + pi/2), cx + length*cos(p[2] + pi/2)]
110: a2y = [cy - length*sin(p[2] + pi/2), cy + length*sin(p[2] + pi/2)]
111:
112: # Plot and save
113: # Axis colors chosen from http://mkweb.bcgsc.ca/colorblind/
114: fig, ax = plt.subplots(figsize=size)
115: ax.plot(x, y, 'k*-', lw=2)
116: ax.plot(a1x, a1y, '-', color='#0072B2', lw=2) # blue
117: ax.plot(a2x, a2y, '-', color='#D55E00') # vermillion
118: ax.plot(cx, cy, 'ko', mec='k')
119: ax.set_aspect('equal')
120: plt.xlim(xmin=minx-b, xmax=maxx+b)
121: plt.ylim(ymin=miny-b, ymax=maxy+b)
122: filename = basename + '.' + format
123: plt.savefig(filename, format=format, dpi=dpi)
124: plt.close()
The key data structure is a list of tuples,1 which represent all of the vertices of the polygon. Each tuple is a pair of (x, y) coordinates for a vertex, and the list must be arranged so the vertices are in consecutive clockwise order. This ordering is the result of Green’s theorem, which is the source of the formulas.2
Here’s a brief example of using the module:
python:
1: #!/usr/bin/env python
2:
3: from section import summary, outline
4:
5: shape = [(0, 0), (5, 0), (5, 1), (3.125, 1), (2.125, 3), (0.875, 3), (1.875, 1), (0, 1)]
6: print(summary(shape))
7: outline(shape, 'skewed', format='png', size=(8, 6))
Line 5 defines the vertices of the shape. The printed output from Line 6 is
Area
A = 7.5
Centroid
cx = 2.3333333333333335
cy = 1.0
Moments and product of inertia
Ixx = 5.0
Iyy = 11.367187499999993
Ixy = -1.666666666666666
Principal moments of inertia and direction
I1 = 11.77706657483349
I2 = 4.590120925166502
θ︎ = 76.18358042418826°
and the PNG file created from Line 7, named skewed.png, looks like this
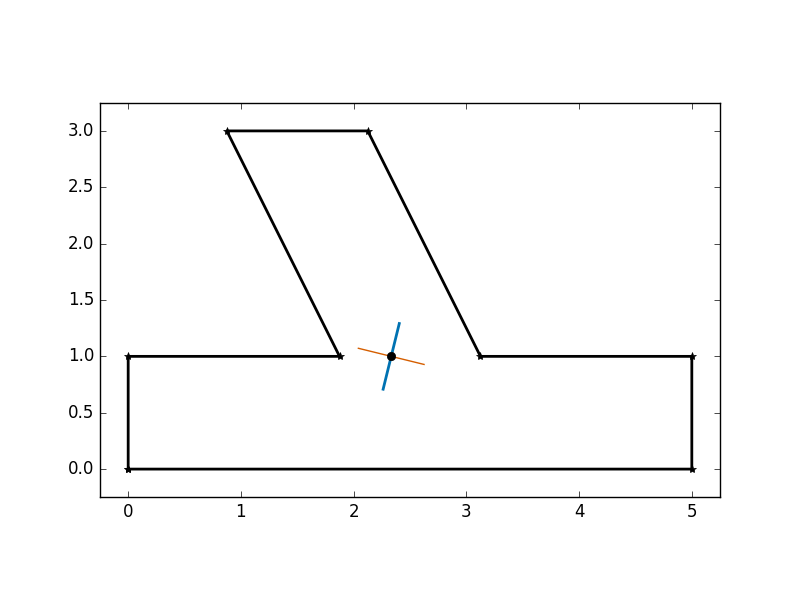
As you might expect, the x-axis is horizontal and the y-axis is vertical. In addition to the shape itself, the outline function also plots the centroid as a black dot and the orientation of the principal axes. The major axis is the thicker bluish line and the minor axis is the thinner reddish line.
The outline function is the most interesting, in that it isn’t just the transliteration of a formula into Python. Lines 92–95 extract the extreme x and y values, and Line 98 calculates the size of a whitespace border (5% of the larger dimension) to keep the frame of the plot a reasonable distance away from the shape. This also makes it easy to crop the drawing to omit the frame. The ends of the principal axes are calculated in Lines 106–110 to make their lengths 20% of the smaller dimension; the idea is to make them long enough to see but not so long as to be distracting.
As noted in the comments, I chose the axis colors from a colorblind-safe palette given by Martin Krzywinski on this page. He got the palette from a paper by Bang Wong that I didn’t feel like paying $59 for (my scholarship has its limits). To better emphasize which is the major principal axis, I made it thicker.
Mechanical and civil engineers learn how to calculate section properties early on in their undergraduate curriculum, so it’s not a particularly difficult topic, but there is a surprising depth to it. Enough depth that I plan to milk it for three more posts, which I’ll link to here when they’re done.
-
Strictly speaking, any data structure that indexes like a list of tuples—a list of lists, for example—would work just as well, but because coordinates are usually given as parenthesized pairs, a list of tuples seemed the most natural. ↩
-
As promised, we’ll get to the derivation of the formulas in a later post, but if you want a taste, here’s a good derivation of the area formula by apnorton. ↩

