Next post Previous post

FFFFFFFFFFF…

December 22, 2018 at 10:25 PM by Dr. Drang

The Great Internet Mersenne Prime Search just announced a new king of prime numbers:

2 82,589,933−1

It’s the 51st Mersenne prime and the 17th discovered using GIMPS software. Readers of ANIAT are likely to have heard about it though John D. Cook’s blog or through a tweet of his that John Siracusa retweeted. The thing that struck me in Cook’s blog and tweet was this:

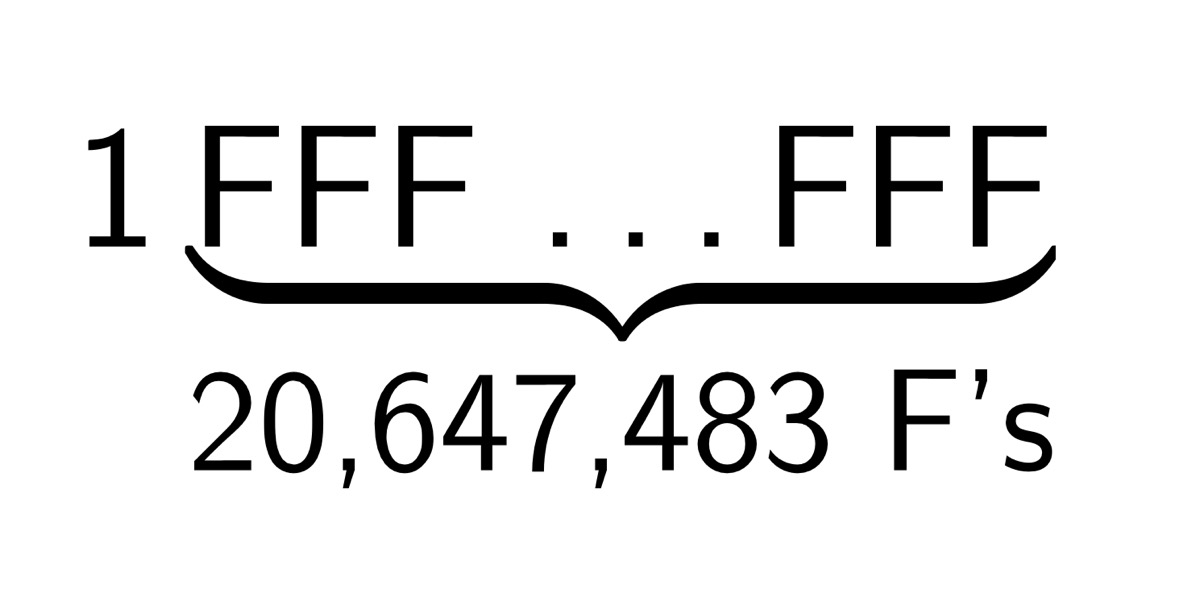
Written in hexadecimal the newly discovered prime is Mersenne prime in hex

That’s a lot of Fs. After a little thinking, I realized that all Mersenne primes (except for the very smallest) are more or less of this form when written in hex: a single digit—either a 1 or a 7—followed by a bunch of Fs.

And it’s not hard to see why. A Mersenne prime is a prime number that can be expressed this way:

2 p−1

where p is itself a prime number. In binary, this number will be a string of p ones. As an example, here’s the 8th Mersenne prime, discovered by my favorite mathematician, Leonard Euler, in the late 1700s:

2 31−1=2,147,483,647

This is a number that should ring a bell with programmers, especially those who spent a lot of time working on 32-bit machines. It’s the largest signed 32-bit integer in two’s complement.

In binary, Euler’s prime looks like this:

1111111111111111111111111111111

I’ve grouped the bits in clusters of four starting at the least significant bit because that’s the key to why the hexadecimal representation is mostly Fs: every one of those clusters of four 1s becomes an F when we switch from binary to hex. Thus, the hex representation for Euler’s prime is

7FFFFFFF

with the leading 7 coming from the three 1s in the most significant bits.

The leading hex digit is always a 1 or a 7 because the number of 1s in the binary representation, p, is a prime number. After dividing p by four to get the number of Fs, the remainder will have to be either one or three.

1 A binary 1 is a hex 1, and a binary 111 is a hex 7.

What’s true for Euler’s prime number is true for all Mersenne primes except the smallest two—3 and 7—which are the only Mersenne primes that have a single-digit hex representation.

So our new friend, 2 82,589,933−1, in hex is a 1 followed by 20,647,483 Fs because 82,589,933 divided by 4 is 20,647,483 with a remainder of 1.

I will leave it as an exercise for the reader to determine a similar rule for the octal representation of a Mersenne prime.

  1. A remainder of zero would mean p is divisible by 4—which it can’t be because it’s prime. A remainder of two would mean p is even—also a no-no for a prime. ↩

Next post Previous post