Galileo and failure
November 30, 2019 at 11:14 AM by Dr. Drang
Last week’s episode of the 99% Invisible podcast was about failure and the problems that arise when we try to design safety systems to prevent failure. I found myself disagreeing with a lot of what was said, but a particular example struck me as flatly wrong. As I looked into it in more detail, I learned that it was wrong for more reasons than I originally thought.
The episode was not produced by the usual 99% Invisible team. It was one of Tim Harford’s Cautionary Tales shows with a 99PI frame around it. My main problem with the show was that its thesis—Safety systems add complexity, and that complexity may lead to failure—was overemphasized to such an extent that it transformed into the more fatalistic Safety systems add complexity which leads to failure. The examples given in the show of failures caused by the introduction of complexity were, I thought, too glibly1 presented.
To be fair, I’ve been investigating failure professionally for three decades, and it may be that no simplified journalistic approach to the topic of failure would have satisfied me. But there is a line between justified simplification and misleading oversimplification, and one of the show’s examples went over that line.
Here’s how it was introduced (from 99PI’s transcript):
Tim Harford:
Galileo Galilei is known for his astronomy and because his work was consigned to the church’s ‘Index Librorum Prohibitorum’, the list of forbidden books, but the great man’s final work opens with a less provocative topic, the correct method of storing a stone column on a building site. Bear with me, this book from 1638 is going to explain the Oscar fiasco and much more.Galileo Galilei:
“I must relate a circumstance which is worthy of your attention as indeed are all events, which happen contrary to expectation, especially when a precautionary measure turns out to be a cause of disaster.”Tim Harford:
A precautionary measure turns out to be a cause of disaster. That’s very interesting, Galileo, please go on.Galileo Galilei:
“A large marble column was laid out so that its two ends rested each upon the piece of beam.”Tim Harford:
I can picture that in my mind, support the column while it’s being stored horizontally ready for use. If you lay it on the ground it may get stained and you’ll probably break it when you try to get ropes underneath it to pull it upright. So yes, store it flat but propped up by a support at one end and a support at the other. But what if the column can’t support its own weight like that and simply snaps in half? Galileo has thought of that.Galileo Galilei:
“A little later it occurred to a mechanic that in order to be doubly sure its not breaking in the middle, it would be wise to lay a third support midway. This seemed too all an excellent idea.”Tim Harford:
Yes. If two supports are good, surely three supports are better.Galileo Galilei:
“It was quite the opposite, for not many months passed before the column was found cracked and broken exactly above the new middle support.”Tim Harford:
How did that happen?Galileo Galilei:
“One of the end supports had after a long while become decayed and sunken, but the middle one remained hard and strong, thus causing one half of the column to project in the air without any support.”Tim Harford:
The central support didn’t make the column safer. It pressed into it like the central pivot of a seesaw snapping it in half. Galileo’s tale isn’t really about storing columns and neither is mine. It’s about what I’m going to call Galileo’s principle, the steps we take to make ourselves safe sometimes lead us into danger.
I first heard this while driving my car to work and thought “That doesn’t sound right.” I paused the podcast and thought about it some more: “No, it isn’t right.” But it’s easy to lose terms when you’re doing algebra in your head, so when I got to work I sketched out the two ways of supporting the column and redid the work. Harford (and Galileo?) were still wrong: the stress in the column with a central support is no larger than the stress in the column with end supports. There’s no reason to believe that putting in a central support made things worse.
It’s easy to see why, but we need a few preliminaries:
- When a column is resting horizontally, it’s being bent by its own weight and the reaction forces at the supports. Therefore, it’s acting more like a beam than a column, and I will refer to it as a beam.
- The stresses in a beam are related to the bending moments in that beam. The stresses will be highest where the bending moments are highest (in absolute value).
- Structural engineers use a sign convention for bending moments: those that put the bottom of a beam in tension and top of the beam in compression are taken as positive; those that put the bottom of the beam in compression and the top of the beam in tension are taken as negative.
- Stone is strong in compression but weak in tension. All other things being equal, it will fail where the tension is the highest.
For the purposes of this post, all of these will be taken as given. I’ve discussed bending moments and stresses in beams briefly here and here, but you can find better treatments in any strength of materials book.
Here’s Galileo’s beam with supports at its ends and the associated moment diagram:

The moment diagram is parabolic and positive along the entire length of the beam. If we call the beam’s weight per unit length , then the peak moment at the center of the beam is
and if the beam were to fail, we would expect it to fail starting at the bottom center where the tension is the highest.
The goal of Galileo’s mechanic was to support the beam in the center as well as at the ends, reducing the maximum (absolute) moment. Here’s what that would look like:

The maximum moment in absolute terms is still at the center, but now it’s a negative moment with this magnitude:
This is one-fourth of the moment when the beam has just end supports, so the mechanic’s action makes sense.
Unfortunately, one of the end supports gave way, leading to this condition:

I’ve drawn the middle support as being a bit off-center; we’ll see why in a bit.
The maximum moment in absolute terms is at the middle support and is negative:
The largest value of the overhang length, , is . Any longer than that and the beam will tip clockwise, with the left end lifting off its support and the right end coming to rest on its lowered support. For the purposes of calculating the maximum moment, this would be structurally equivalent to (albeit a mirror image of) what we’ve shown above.
Setting to its maximum value of , we get
This is exactly the same as the maximum moment with supports at the ends of the beam. The only difference is that this beam will start fracturing on the top surface (as Galileo said) instead of at the bottom surface.
So why didn’t the beam crack before the mechanic put in the middle support? I can think of a few reasons:
- Because stone isn’t uniform in strength, it may be that the top of the beam is a bit weaker than the bottom. If so, a beam that’s just barely able to survive a high positive moment will fail when it sees a high negative moment of the same magnitude. This means that the beam’s survival when it was briefly on two end supports only was pure luck. If it had been set down with the weak side on the bottom, it would have failed then.
- There is some time dependence to the cracking of the stone. If so, the beam would have cracked eventually on its two end supports.
- The story is slightly off, and the mechanic had the middle support in place right from the start.
- The whole story is just made up, either by Galileo or whoever told it to him.
None of these scenarios support the idea that what the mechanic did was add complexity that caused the failure.

I got curious about why Galileo even told this story. It’s in his Dialogues Concerning Two New Sciences (that’s an affiliate link), and is part of an introduction to the square-cube law. It’s preceded by
Thus, for example, a small obelisk or column or other solid figure can certainly be laid down or set up without danger of breaking, while the very large ones will go to pieces under the slightest provocation, and that purely on account of their own weight.
and succeeded by
This is an accident which could not possibly have happened to a small column, even though made of the same stone and having a length corresponding to its thickness, i.e., preserving the ratio between thickness and length found in the large pillar.
But the story of the inserted middle support has nothing to do with the square-cube law. It’s not a story about small structures being better able to support their own weight than large structures. Even weirder, Galileo knew perfectly well that the beam with half its length overhanging a support had the same strength as one supported at its ends. Later on in the book, near the end of the second day,2 Galileo explicitly explains this:
Hitherto we have considered the moments and resistances of prisms and solid cylinders fixed at one end with a weight applied at the other end; three cases were discussed, namely, that in which the applied force was the only one acting, that in which the weight of the prism itself is also taken into consideration, and that in which the weight of the prism alone is taken into consideration.
He’s referring to an earlier discussion on the behaviour of cantilever beams. Here’s the charming drawing that goes along with that portion of the book:
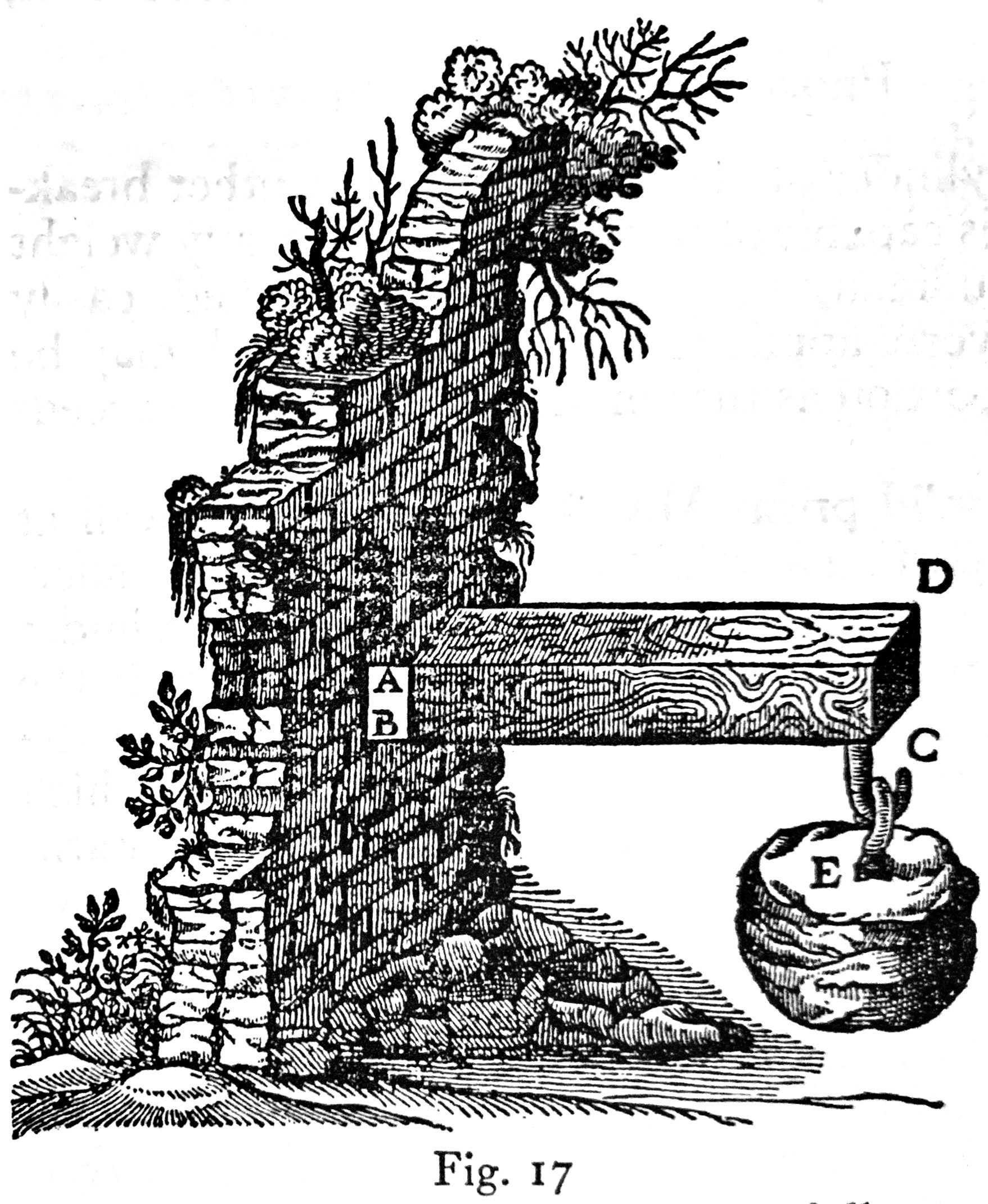
Let us now consider the same prisms and cylinders when supported at both ends or at a single point placed somewhere between the ends.
Here’s the drawing that goes with the new discussion:
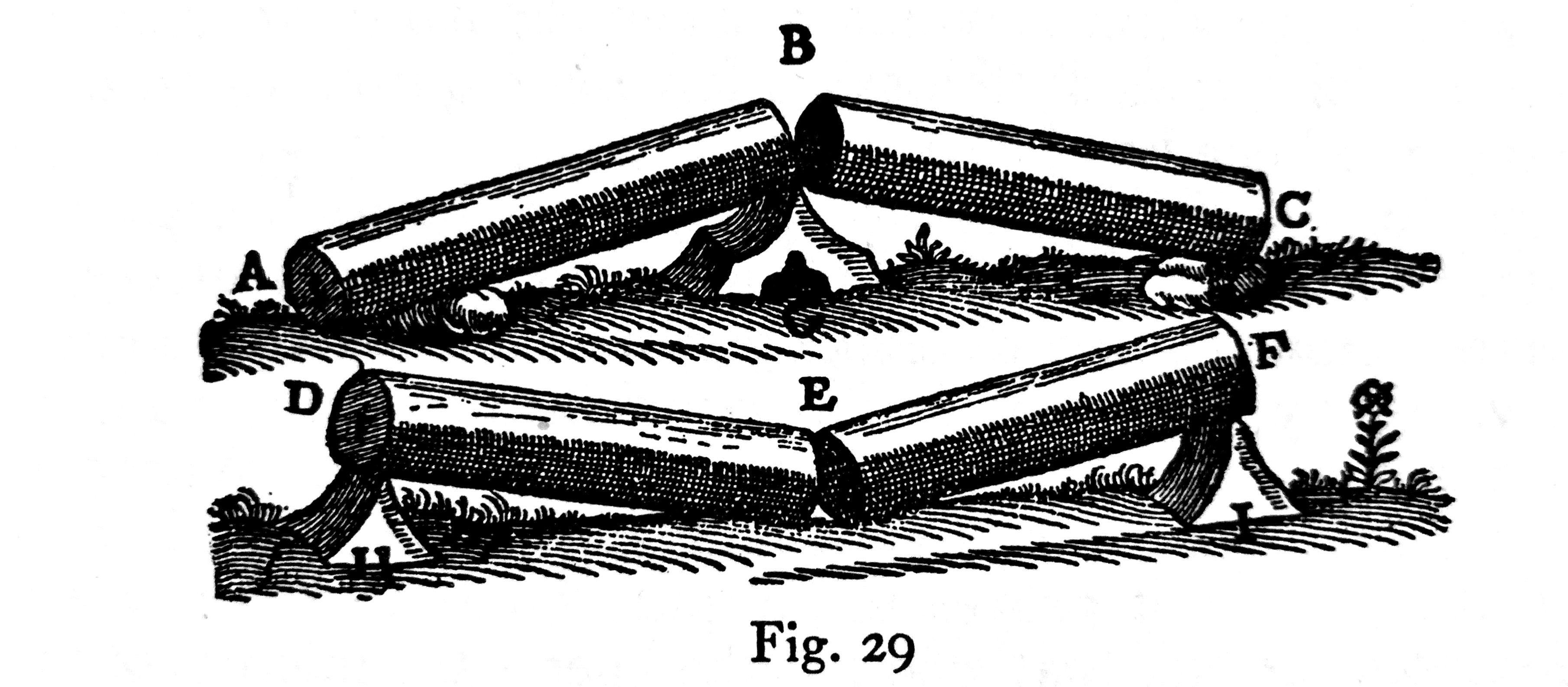
I should point out that for the situation in which the right support has sunk out of the way and the middle support is at exactly , the reaction at the left support will be zero, so it’s as if the beam were balanced on the central support, as Galileo shows in the upper drawing.
Here’s the nut:
In the first place, I remark that a cylinder carrying only its own weight and having the maximum length, beyond which it will break, will, when supported either in the middle or at both ends, have twice the length of one which is mortised into a wall and supported only at one end.
There you have it. The maximum length of a beam that’s balanced on a support at its center is equal to the maximum length of a beam that’s on supports at both ends. Both of them are twice the maximum length of a cantilever beam.
For completeness, here’s his explanation. It’s tough sledding.
This is very evident because, if we denote the cylinder by ABC and if we assume that one-half of it, AB, is the greatest possible length capable of supporting his own weight with one end fixed at B, then, for the same reason, if the cylinder is carried on the point G, the first half will be counterbalanced by the other half BC. So also in the case of the cylinder DEF, if its length be such that it will support only one-half this length when the end D is held fixed, or the other half when the end F is fixed, then it is evident that when supports, such as H and I, are placed under the ends D and F respectively the moment of any additional force or weight placed at E will produce fracture at this point.
In the introduction to Two New Sciences, the translators, Henry Crew and Alfonso de Salvio, say that they have “made this translation as literal as is consistent with clearness and modernity.” We may take it, then, that Galileo wrote like a patent attorney.
Having gone through all of the second day and a good chunk of the first day of Two New Sciences, I still have no idea why Galileo included the story of the column and the mechanic. It has nothing to do with the topic being covered where he included it, and it doesn’t match his own (generally correct) understanding of the strength of beams. I wonder if it was written before he’d done the work on the maximum length of beams, and he just never went back to check it.
I think we can forgive Galileo this lapse. He was creating new knowledge and, given his trouble with the Vatican, was desperate to get it published. Editing was of secondary concern at best.
I’m less forgiving of Tim Harford. Anyone who’s taken a statics class could have told him that the story on which he was basing “Galileo’s Principle” didn’t demonstrate that principle.
