Next post Previous post

A little more on Galileo’s column

December 7, 2019 at 9:43 AM by Dr. Drang

After last week’s post, I thought some more about Galileo’s column problem. The mechanic in Galileo’s story tried to reduce the bending stress when the column is being stored on its side by inserting a third support. A simpler way would be to keep two supports but change the spacing between them. Let’s see how to do that in a way that minimizes the bending stress.

Here’s a uniform beam with supports set in a distance aa from its ends. Below it is the corresponding bending moment diagram.

Beam with symmetric overhangs

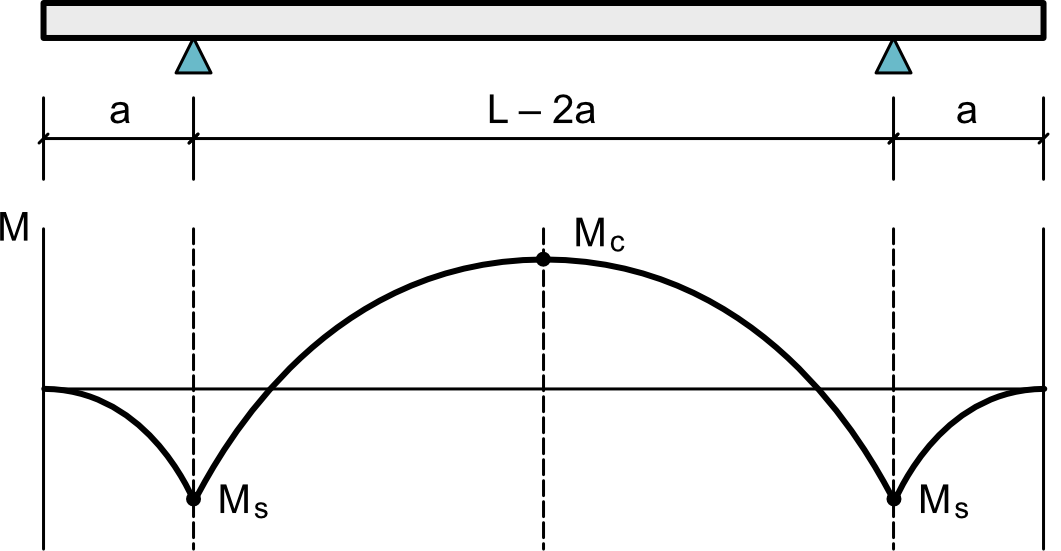
The moment at the supports is

Ms=−wa22M_s = -\frac{w a^2}{2}

and the moment at the center is

Mc=w(L−2a)28−wa22M_c = \frac{w(L-2a)^2}{8} - \frac{w a^2}{2}

As we discussed last time, the difference between positive and negative moments is whether the tension—and therefore where the cracking starts—is on the bottom or top of the beam. In assessing the overall strength of the beam, top and bottom cracking are equivalent, so we don’t have to worry about the sign of moment, only its magnitude.1 We want to find the value of aa that minimizes the maximum moment in absolute terms.

Seeing the word “minimize” might make you think it’s time to do some calculus, but let’s try a different approach. Note that for small values of aa, |Ms||M_s| increases and McM_c decreases with increasing aa. As we increase aa, there will be a point at which the two are equal. This will minimize the maximum absolute moment in the beam.

So we set

wa22=w(L−2a)28−wa22\frac{w a^2}{2} = \frac{w(L-2a)^2}{8} - \frac{w a^2}{2}

and solve for aa. To nondimensionalize the equation, let’s use the substitution x=a/Lx = a/L to get

wL2(x2)=wL2[(1−2x)28−x2]wL^2 \left( \frac{x}{2} \right) = wL^2 \left[ \frac{(1 - 2x)^2}{8} - \frac{x}{2} \right]

Expanding, canceling, and rearranging gives us

4x2+4x−1=04x^2 + 4x - 1 = 0

which we can solve by completing the square or through the quadratic formula. Either way, we get two solutions:

x=−12(2+1)x = -\frac{1}{2}(\sqrt{2} + 1)

and

x=12(2−1)x = \frac{1}{2}(\sqrt{2} - 1)

The first solution is negative and can be ignored as a mathematical artifact. The second is the solution we want. It’s approximately x=0.207x = 0.207 and gives a maximum absolute moment in the beam of Mmax=0.0214wL2M_{max} = 0.0214 wL^2. Compare this with the maximum moment with the supports at the ends (0.125wL20.125 wL^2) and you can see how much value there is in moving the supports in.

If we plot MmaxM_{max} against aa, we can see why calculus wouldn’t have helped us find the miminum. The smallest value of MmaxM_{max} is at a cusp, the intersection of the lines for McM_c and MsM_s. Setting a derivative equal to zero won’t locate that point.

Maximum moment vs overhang

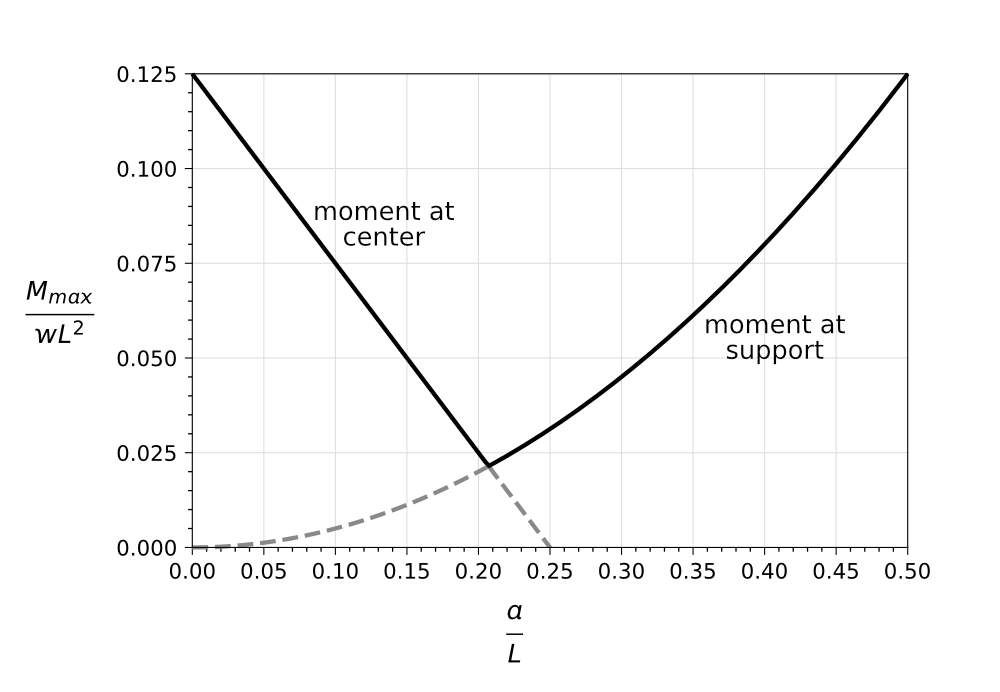
Note that the graph also shows us something we looked at in the previous post: the maximum moment when the beam is balanced over a support at the center is the same as when it’s supported at its ends.

Apart from being a fun little problem to think about, Galileo’s column illustrates an important concern in structural engineering. Structural elements that would survive perfectly well in the completed structure sometimes fail during construction because they see loading during assembly (or storage or transportation) that they’ll never see afterward. Although engineers’ main concern is how the elements behave when the building is complete, they also have to account for the stresses that arise before then.

  1. This is not true in general, but it is true for beams in which the upper and lower halves of the cross-section are symmetric. Recall that this beam is intended to be tilted up and used as a column, which means its cross-section is either circular or circular with flutes and has the required symmetry. ↩

Next post Previous post