Next post Previous post

Lagrange and the JWST

January 24, 2022 at 6:39 PM by Dr. Drang

The James Webb Space Telescope reached its destination today. Since its launch a month ago, there’s been a lot of explanation on space-centric sites of what and where the Lagrange points are. Most of these have neat animations or other graphics, and they all talk about how L2 (the JWST’s Lagrange point) is about 1.5 million kilometers. But they tend to avoid the math that explains why L2 is at that distance. Longtime readers of ANIAT know that avoiding the math is not what I do here.

Longtime readers of ANIAT also know that I’ve written about Lagrange points a few times already. In one of those, I showed how to find all five Lagrange points and included one of my favorite graphs.

Contour lines for Lagrange points

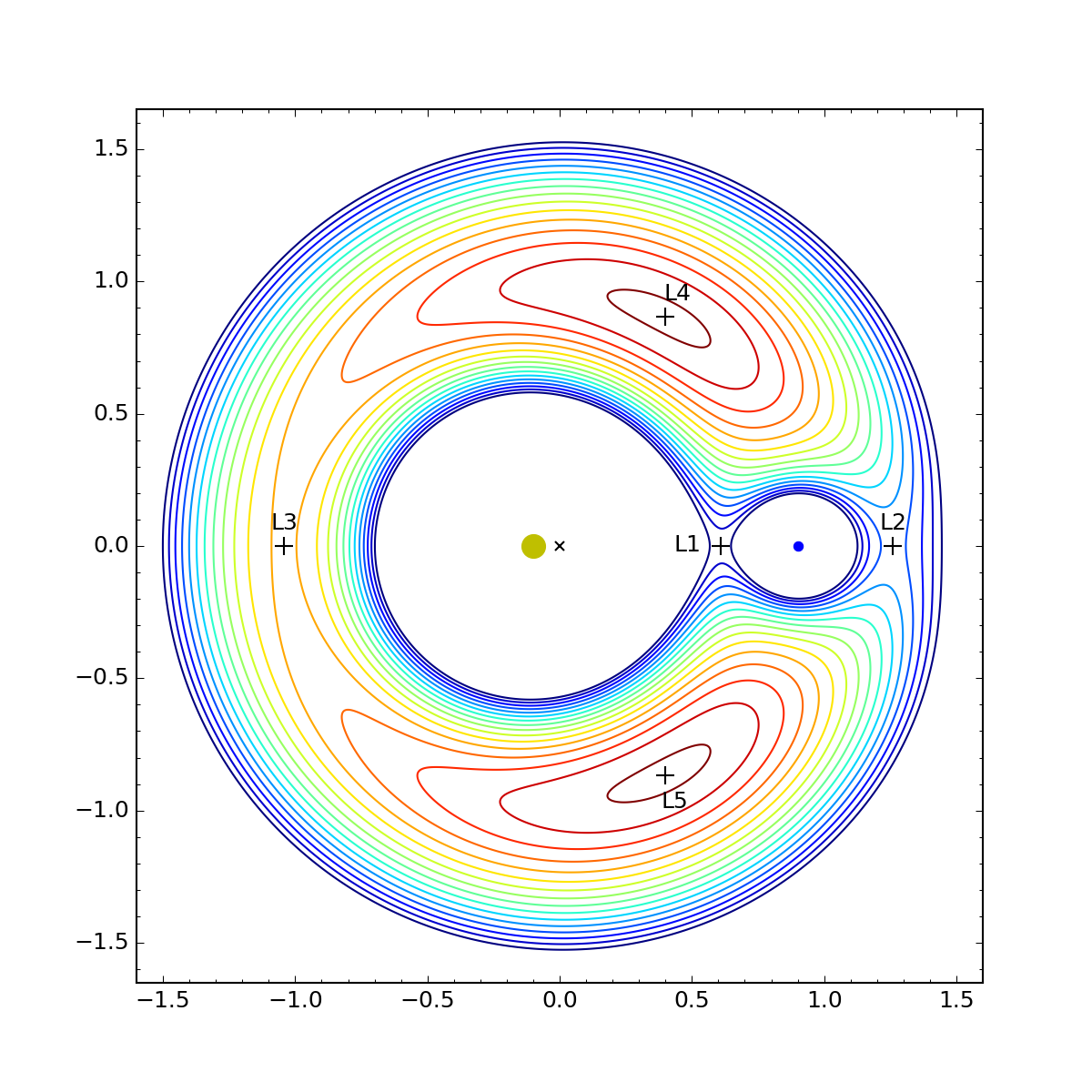
This is a contour plot of the potential energy of a small satellite, and the stationary points (i.e., points where the slope is zero) are the Lagrange points. The great thing about doing an energy-based solution is that you don’t have to know roughly where the Lagrange points are before you start—their existence and positions fall out of the analysis naturally. The downside is that the math gets complicated.

So let’s cheat to make the math simpler. We know the L2 point is beyond Earth’s orbit on the line that connects the Sun and the Earth. We’ll start there and figure out how far out from the Earth it is.

Here’s the layout:

Lagrange point 2

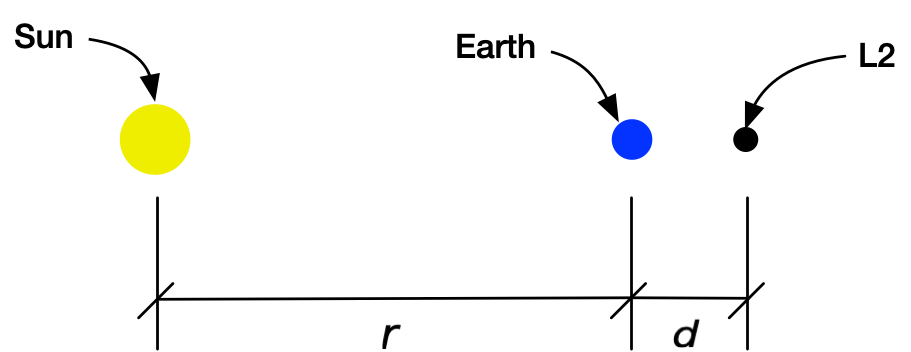
The orbits of the Earth and L2 are assumed circular (pretty close to true), and whatever is at L2 is taken to be so small that it doesn’t interfere with the Earth’s orbit in any measurable way (definitely true).

Let’s start by looking at the Earth’s orbit. Newton’s second law says the force acting on the Earth is equal to its mass times its acceleration. The force comes from Newton’s law of gravitation,

GMmr2\frac{G M m}{r^2}

where GG is the universal gravitational constant, MM is the mass of the Sun, mm is the mass of the Earth, and rr is the distance between the two. The force is directed toward the Sun. Because the Earth is taken to be moving in a circle of radius rr at constant angular velocity, its acceleration is

rω2r \omega^2

where ω\omega is the angular velocity. Like the force, this acceleration points toward the Sun.

Putting these together, we get

GMmr2=mrω2\frac{G M m}{r^2} = m r \omega^2

and so

ω2=GMr3\omega^2 = \frac{G M}{r^3}

Now let’s look at our satellite at L2. It’s seeing two gravitational forces, one from the Sun

GMm~(r+d)2\frac{G M \tilde{m}}{(r + d)^2}

and one from the Earth

Gmm~d2\frac{G m \tilde{m}}{d^2}

where m~\tilde{m} is the mass of the satellite. By definition, L2 orbits at the same angular velocity, ω\omega, as the Earth, so

GMm~(r+d)2+Gmm~d2=m~(r+d)ω2=m~(r+d)GMr3\frac{G M \tilde{m}}{(r + d)^2} + \frac{G m \tilde{m}}{d^2} = \tilde{m} (r + d) \omega^2 = \tilde{m} (r + d) \frac{G M}{r^3}

We’re now going to introduce a couple of nondimensional quantities:

Plugging these definitions into the equation for the satellite lets us eliminate mm and dd to get

GMm~r2(1+δ)2+GMμm~δ2r2=m~r(1+δ)GMr3\frac{G M \tilde{m}}{r^2 (1 + \delta)^2} + \frac{G M \mu \tilde{m}}{\delta^2 r^2} = \tilde{m} r(1 + \delta) \frac{G M}{r^3}

We can cancel out GG, MM, m~\tilde{m}, and rr from this equation, leaving

1(1+δ)2+μδ2=(1+δ)\frac{1}{(1 + \delta)^2} + \frac{\mu}{\delta^2} = (1 + \delta)

or, after multiplying through by (1+δ)2(1 + \delta)^2,

1+μ(1δ+1)2=(1+δ)31 + \mu \left( \frac{1}{\delta} + 1 \right)^2 = (1 + \delta)^3

From NASA’s Sun Fact Sheet, we see that μ=3.00×10−6\mu = 3.00\times 10^{-6}, a very small number. That means δ\delta will also be a small number, and we can approximate the above equation with

1+μδ2≈1+3δ1 + \frac{\mu}{\delta^2} \approx 1 + 3 \delta

and therefore

μ≈3δ3\mu \approx 3 \delta^3

Plugging in the value for μ\mu gives us

δ≈0.01\delta \approx 0.01

so the distance from the Earth to L2 is one one-hundredth of the distance from the Sun to the Earth. Since the Earth is about 150 million kilometers from the Sun, L2 is about 1.5 million kilometers from the Earth. Which is what everyone has been saying, but now you can prove it.

Next post Previous post