Next post Previous post

Parabola properties

March 11, 2022 at 6:47 AM by Dr. Drang

Last week, John D. Cook wrote a post in which he calculated the area under an inverted catenary curve. As part of the post, he estimated the area under the catenary by calculating the area under a parabola with the same width (41″) and height (39.5″). I’ve reproduced Cook’s plot of the two curves here, but with the vertical and horizontal scales equal so you get a better sense of how tall these arches are.

Catenary and parabola

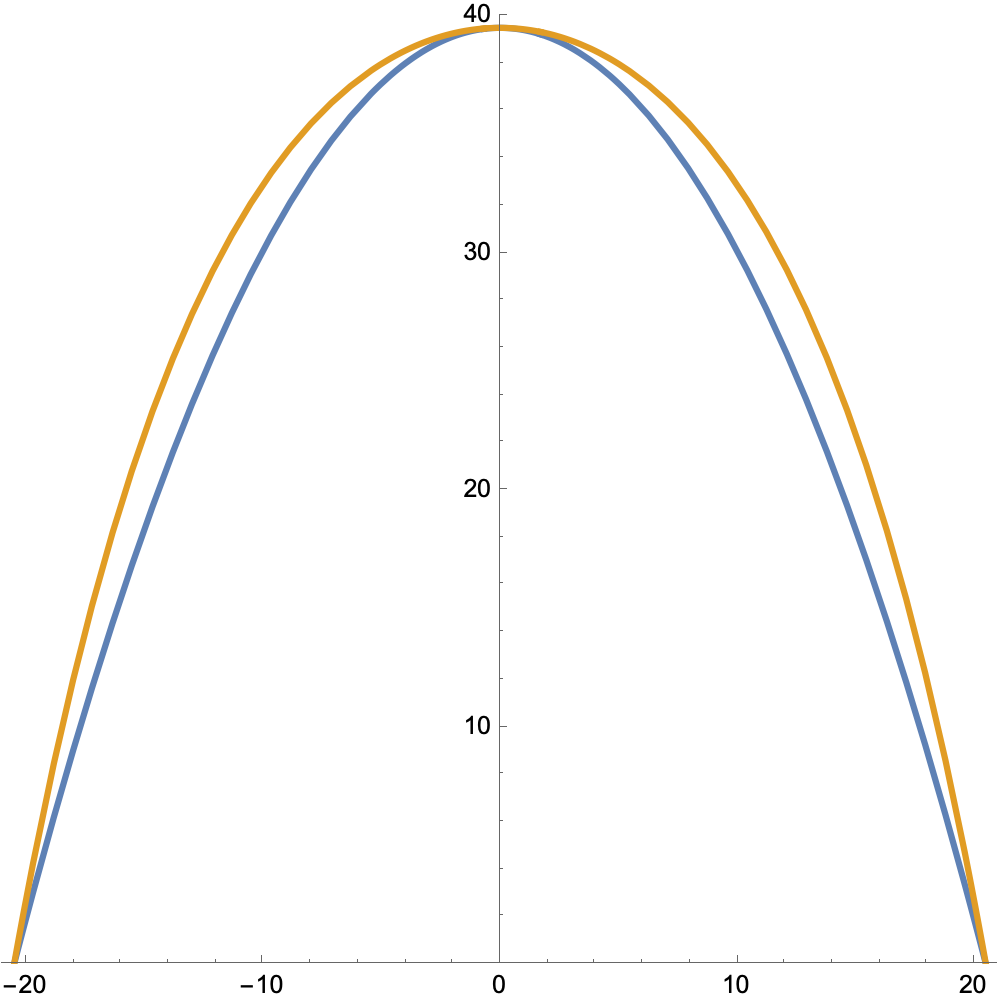
The catenary is the orange curve; the parabola is blue.

Cook’s method of getting the area under the parabola surprised me, which is why I’m writing this post. To plot the parabola—which he did in Mathematica—he had to generate the formula for the curve:

y=h[1−(2xw)2]y = h \left[ 1 - \left( \frac{2x}{w} \right)^2 \right]

where h=39.5h = 39.5 is the height and w=41w=41 is the width.

Once you have this formula defined in Mathematica, it’s very easy to use the Integrate command to get the area under the curve, and I suppose that’s the reason Cook did the calculation that way. But there’s no need for the formula if all you want is the area under the parabola. It’s two-thirds the area of the enclosing rectangle:

A=23wh=23(41)(39.5)=1079.67A = \frac{2}{3}wh = \frac{2}{3}(41)(39.5) = 1079.67

When Cook started looking at using a parabola to approximate the catenary, this is the calculation I thought he would arrive at, for two reasons:

  1. Fast approximations like this are a favorite topic of his.
  2. This formula for the area under a parabola is due to Archimedes and is famous in mathematics because its derivation anticipated integral calculus by nearly 2000 years.

Strictly speaking, Archimedes figured out that the parabola’s area is 4/34/3 that of a particular inscribed triangle,

Parabola and inset triangle

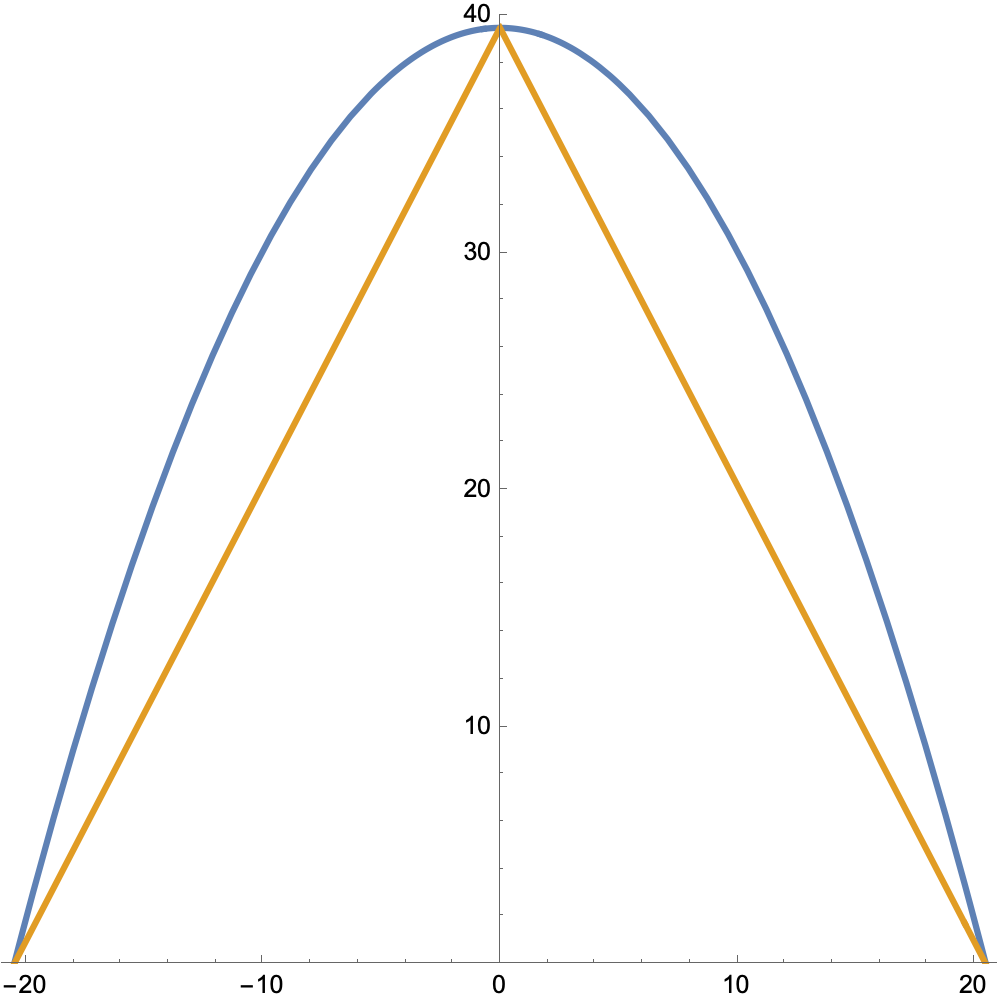
but it’s trivial to see that the area of the inscribed triangle is half that of the enclosing rectangle.1

I learned the two-thirds rule for the area under a parabola not from Archimedes but from Ted Krauthammer and (especially) John Haltiwanger, who were the instructors I had in a pair of structural analysis classes over 40 years ago. For two straight semesters, I solved a seemingly endless series of beam deflection problems using the moment-area method, an analysis technique that relies heavily on knowing the both the area under a parabola and the location of its centroid.

To this day, if you wake me up in the middle of the night and ask me for the properties of a parabola, I will ask for a pencil and sketch out something like this:

Parabola areas and centroids

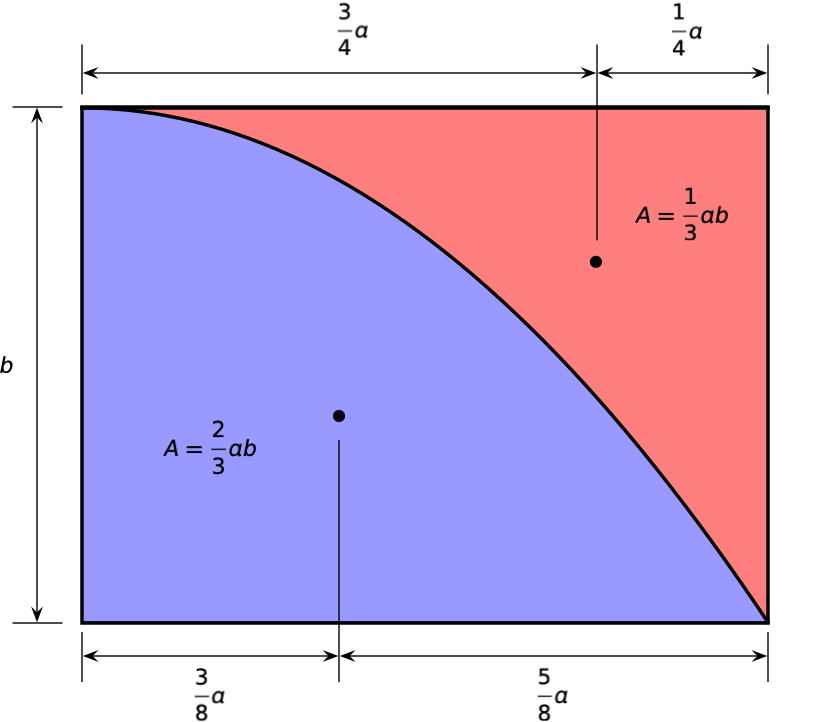
Both the red and blue areas come up in beam deflection problems, so I learned both of them.

Having written this, I now feel committed to two followup posts: one on why a parabola would be a reasonable approximation to a catenary and the other on the moment-area method and how to use it to calculate beam deflections.

  1. It’s worth mentioning that Archimedes didn’t limit himself to symmetric problems like we have here, but it’s usually easier for us mortals to follow the derivation for this simpler setup. ↩

Next post Previous post