Next post Previous post

Octagons and squares

July 12, 2022 at 3:10 PM by Dr. Drang

A recent episode of the 99% Invisible podcast, “Octagon House,” had a little math problem embedded in it, and while I was solving that problem I learned something new about Mathematica.

(By the way, I bought the personal edition of Mathematica earlier this year when it was on sale for about half off. I’m on the cusp of retirement, so I thought I’d give myself a gift that would keep me interested in mathematics when work is no longer providing me math problems. You’ll probably be seeing more Mathematica-related stuff here as time goes on.)

The episode is about the short-lived mid-19th century trend of building houses that are octagonal in plan. The main proponent of such houses was Orson Squire Fowler, who wrote the following in his book, The Octagon House: A Home For All.

Now, since a given length of octagon wall will enclose one-fifth more space than the same length of wall in a square shape, of course, you can have the same size wall for one-fifth less money.

Ignore everything after the “of course.” My interest was in the premise:

Given an octagon and a square of the same perimeter, the ratio of their areas is 6:5.

Could that really be true? I doubted it. Seemed way to simple, and I couldn’t believe it didn’t involve irrational numbers.

I was listening to the podcast while out on a walk,1 so I paused the playback and tried to work out the area ratio in my head. I was in some respects successful, in that I got an answer that I was sure didn’t equal 6/5, but I didn’t know what my answer was numerically. I had an expression that included the tangent of 22.5°, which unfortunately isn’t one of the trig functions I have memorized.2

Here’s how I imagined an octagon and a square with the same perimeter:

Octagon and square

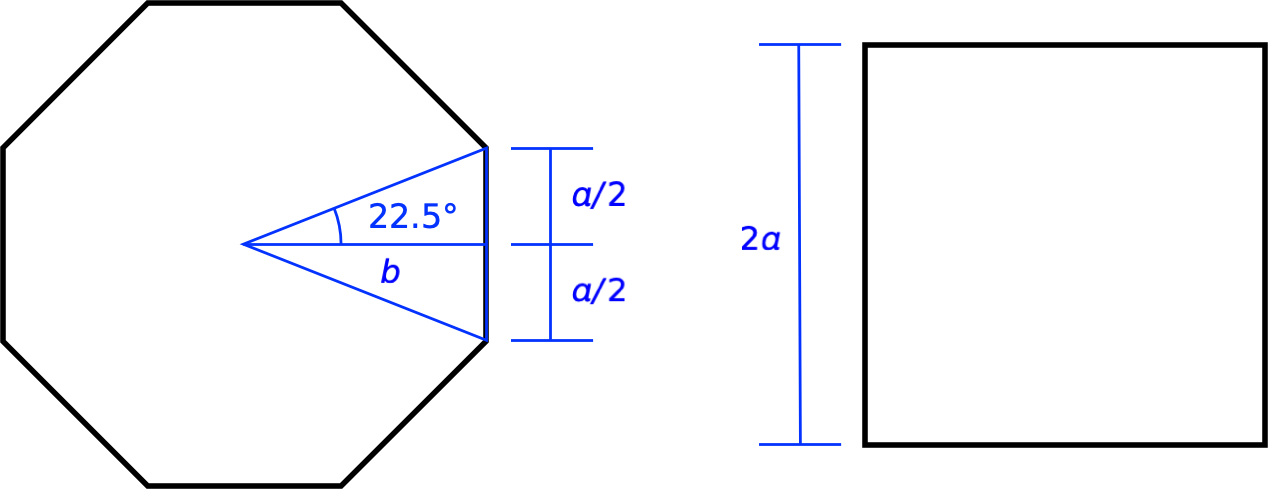
To get the area of the octagon, we figure out the area of one of the interior triangles and multiply by eight. The area of each interior triangle is

Atri=ba2A_{tri} = b \frac{a}{2}

where the base of the triangle is

b=a2tan22.5°b = \frac{a}{2 \tan{22.5°}}

So

Aoct=8Atri=2a2tan22.5°A_{oct} = 8 A_{tri} = \frac{2 a^2}{\tan{22.5°}}

and

AoctAsq=2a2tan22.5°4a2=12tan22.5°\frac{A_{oct}}{A_{sq}} = \frac{\frac{2 a^2}{\tan{22.5°}}}{4a^2} = \frac{1}{2 \tan{22.5°}}

This is where I got stuck. When I got home, Mathematica told me that the area ratio is

12Cot[π8]\frac{1}{2}\;\mathrm{Cot}\left[ \frac{\pi}{8} \right]

which, I was happy to see, matched my result.3 And I knew that I could convert this to a number by enclosing it in N[] or by clicking the “numerical value” button under the last output.

Mathematica output

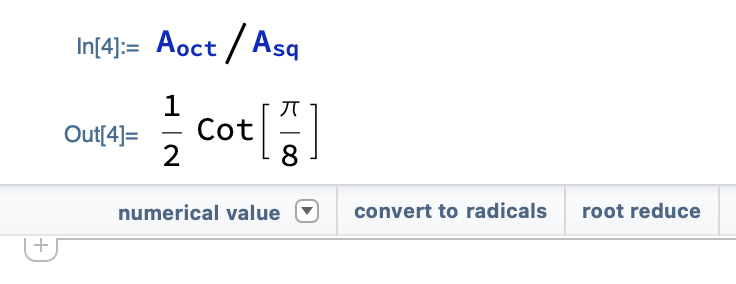
But before getting numbers, I wanted to see what the result was in terms of irrational values. The “convert to radicals” button seemed like the way to go for that. Clicking it gave me

Mathematica further output

It was nice to learn about ToRadicals, but an answer of

122+22−2\frac{1}{2}\; \sqrt{\frac{2 + \sqrt{2}}{2 - \sqrt{2}}}

seemed much more complicated than necessary. I clicked the “root reduce” button in hopes of simplifying the expression. It worked.

Mathematica simplified irrational

So I was right that the area ratio wasn’t simply 6/5, but it was also clear—even before I tapped the “numerical value” button—that

12(1+2)\frac{1}{2}\; \left( 1 + \sqrt{2} \right)

is pretty close to 6/5. It’s 1.2071 (to five digits).

So Fowler was correct, for all practical purposes, and I got to learn Mathematica’s ToRadicals and RootReduce functions.

And in case you’re ever out walking and need to know the tangent of 22.5°, it’s

2−1≈0.4142\sqrt{2} - 1 \approx 0.4142

  1. The only times I listen to podcasts are while driving or walking, neither of which are conducive to working out math problems with either a paper and pencil or Mathematica. ↩

  2. And if you’re wondering why I didn’t use the half-angle formulas, it’s because I don’t have them memorized, either. ↩

  3. Sometime in college, I realized there’s nothing wrong with putting the simpler trig functions in the denominator and stopped using cotangent, secant, and cosecant. Mathematica apparently disagrees with my decision. ↩

Next post Previous post