Next post Previous post

Vintage mechanics

July 21, 2022 at 1:58 PM by Dr. Drang

Last week I read Vintage Murder by Ngaio Marsh and was surprised to find that the setup for the murder was very much like the homework problems I used to assign in my sophomore-level mechanics class. Solving the problem—which didn’t help in solving the murder—was a fun little exercise.

Marsh’s hero, Detective Chief Inspector Roderick Alleyn, is on holiday in New Zealand. An English theatrical company happens to be travelling the same route as Alleyn, and they all stop in some small town on the North Island. Because he’s gotten to know the members of the company, Alleyn is invited to a birthday party for the company’s leading lady, Carolyn Dacres.

As a surprise, Dacre’s husband and the manager/owner of the company, Alfred Meyer, has brought along a jeroboam of champagne and has worked in secret with the stagehands to have it magically revealed at the party, which takes place on stage after a show.

Here’s Marsh’s description of the setup:

The giant bottle was suspended in the flies with a counterweight across a pulley. A crimson cord from the counterweight came down to the stage and was anchored to the table. At the climax of her party, Carolyn was to cut this cord. The counterweight would then rise and the jeroboam slowly descend into a nest of maiden-hair fern and exotic flowers, that was to be held, by Mr. Meyer himself, in the centre of the table.

And here’s my sketch of it. I’ve drawn the cord connecting the bottle to the counterweight in blue to help distinguish it from the cord that’s supposed to get cut.

Bottle setup

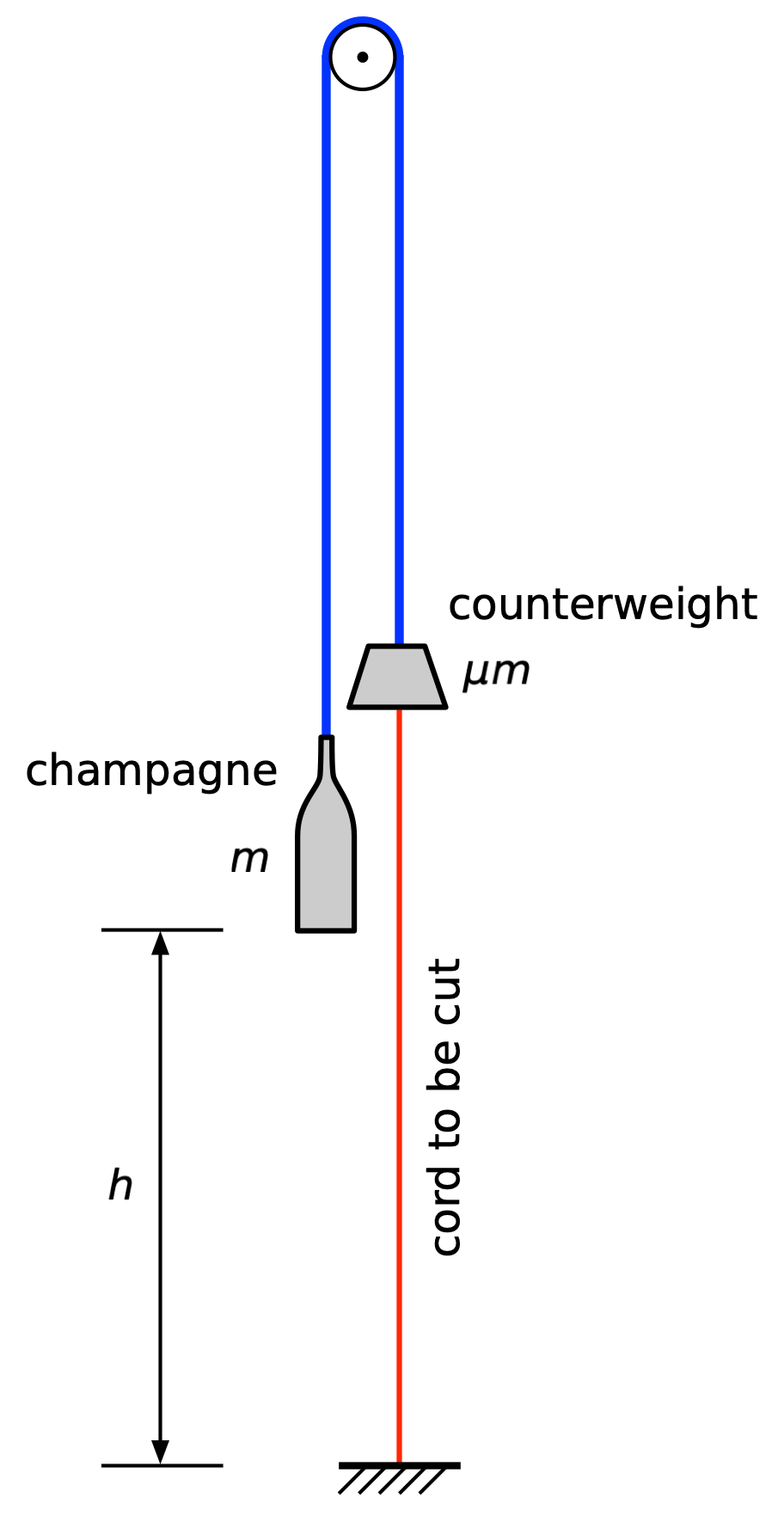
Alfred and the stagehands practiced the cord-cutting several times to make sure the bottle would come down at the right speed and in the right place. But at some point before the party, the murderer removed the counterweight, connected the red and blue cords, and shifted the pulley a couple of feet sideways. When Carolyn cut the red cord, the jeroboam fell rapidly and smashed into poor Alfred’s head, killing him instantly and ruining the party.

The dynamics of the altered setup aren’t very interesting, but the dynamics of the original setup are. As a homework problem, this could be assigned in two ways:

  1. Given the masses of the jeroboam and the counterweight, determine the downward acceleration of the jeroboam when the red cord is cut.
  2. Given the masses of the jeroboam and the counterweight and the height of the jeroboam above the table, determine the downward velocity of the jeroboam just before it reaches the table.

Let’s solve both. We’ll make the usual sophomore-level assumptions that the following values are negligible and can be ignored in the analysis:

The acceleration problem is best solved using Newton’s Second Law. We’ll start with the free-body diagrams of the bottle (I’m tired of typing jeroboam) and the counterweight.

Free-body diagrams

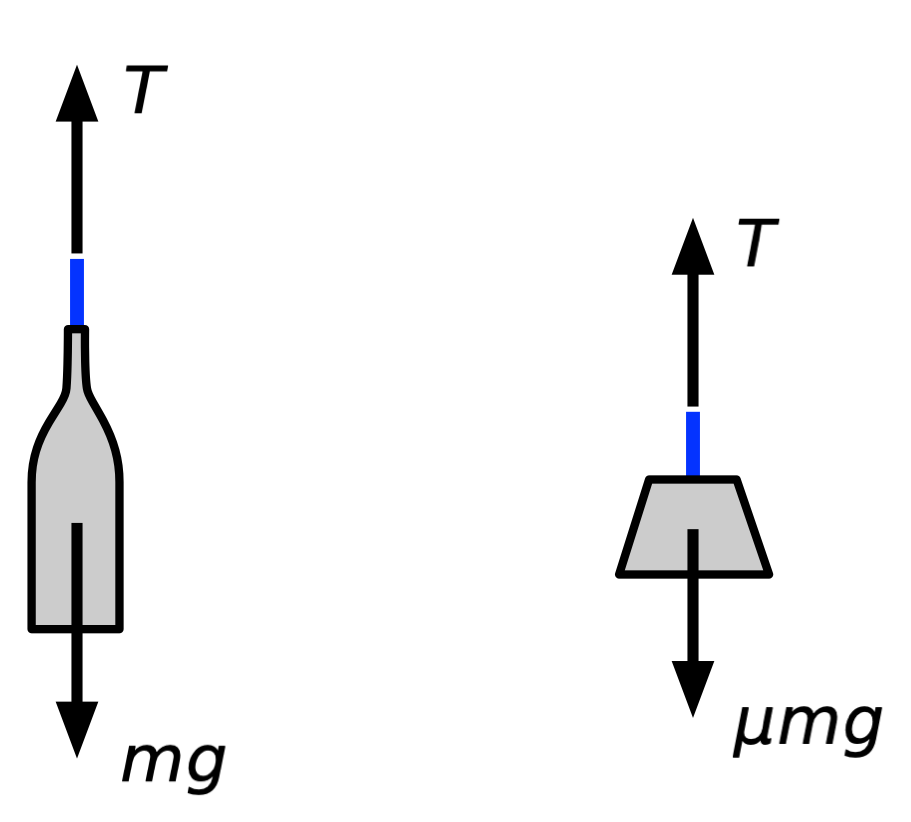
gg is the acceleration due to gravity. mm is the mass of the bottle. μ\mu is the mass ratio of the counterweight to the bottle; it’s a dimensionless parameter that’s less than one. TT is the tension in the blue cord, which is equal on both sides of the pulley because of the assumptions above.

Applying Newton’s Second Law to the bottle FBD, and taking the positive direction to be downward, we get

mg−T=ma⟹T=m(g−a)mg - T = ma \quad \Longrightarrow \quad T = m \left( g - a \right)

where aa is the downward acceleration of the bottle.

Note that the blue cord provides a kinematic constraint that makes the downward movement—displacement, velocity, and acceleration—of the bottle equal to the upward movement of the counterweight. Using this, Newton’s Second Law applied to the counterweight, with the positive direction upward, is

T−μmg=μma⟹T=μm(a−g)T - \mu m g = \mu ma \quad \Longrightarrow \quad T = \mu m \left( a - g \right)

Therefore

m(g−a)=μm(a−g)m \left( g - a \right) = \mu m \left( a - g \right)

and

a=g1−μ1+μa = g \frac{1 - \mu}{1 + \mu}

This is an nice, neat little solution, and it makes sense at the two extremes:

You might feel uncomfortable about my flipping the coordinate system around—down is positive for the bottle, up is positive for the counterweight. Don’t. We are in charge of the coordinate systems we use, not the other way around. We just have to stay consistent within the equations for each free-body diagram, which we did.

Now let’s move on to the velocity problem. We could take the acceleration result we just got and do some kinematics, but it’s more fun to use energy principles. Also, when the homework problem has things moving up or down and asks for velocity, it’s a good bet that your professor wants you to solve the problem using energy.

Before the red cord is cut, the bottle and counterweight are at rest and the kinetic energy of the system is zero. When the bottle reaches the level of the table, when both it and the counterweight are traveling at a speed of vv, the kinetic energy is

12mv2+12μmv2=12mv2(1+μ)\frac{1}{2} m v^2 + \frac{1}{2} \mu m v^2 = \frac{1}{2} m v^2 \left( 1 + \mu \right)

Because we start at zero, this is also change in kinetic energy.

There are no springs in the system, so the potential energy is all due to gravity. The bottle loses potential energy as it goes down, and the counterweight gains potential energy as it goes up. The overall change in potential energy of the system is

−mgh+μmgh=−(1−μ)mgh-mgh + \mu mgh = - \left( 1 - \mu \right) m g h

I’ve written this with a leading negative sign to emphasize that we have a loss of potential energy because the bottle weighs more than the counterweight.

The gain in kinetic energy must equal the loss in potential energy, so

12mv2(1+μ)=(1−μ)mgh\frac{1}{2} m v^2 \left( 1 + \mu \right) = \left( 1 - \mu \right) m g h

and, after a little algebra,

v=2gh1−μ1+μv = \sqrt{2gh} \sqrt{\frac{1 - \mu}{1 + \mu}}

This solution also makes sense at the extremes. You may not remember that an object dropped from a height of hh hits the ground at a speed of 2gh\sqrt{2gh}, but that is the well-known result.

This is fine as far as the homework-style problems are concerned, but Alfred and the stagehands had to solve the inverse problem: What counterweight is necessary to get the bottle to reach the table at a gentle speed? For that, we just rearrange the above solution to solve for μ\mu:

μ=2gh−v22gh+v2\mu = \frac{2gh - v^2}{2gh + v^2}

Let’s apply some numbers to this and see what we get. I would put the original height of the bottle at 4 m above the table, and I doubt Alfred would want the bottle moving faster than 1 m/s when it reaches the table. With those values, and the usual gravitational acceleration, we get

μ=2·9.81·4−122·9.81·4+12=0.9748\mu = \frac{2\cdot 9.81 \cdot 4 - 1^2}{2\cdot 9.81 \cdot 4 + 1^2} = 0.9748

So the counterweight had better be pretty damned close to the weight of the bottle, which is in the 10–11 pound range. You would think the stagehands would have to cobble together a few weights to hit this target, but the book says it was just a single counterweight—an item that was up in the flies and would normally be used to help lift scenery. How the company happened to have a counterweight of exactly this size is a mystery even DCI Alleyn couldn’t solve.

Next post Previous post