And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

Underscore David Smith and linearization for large angles

February 25, 2023 at 1:46 PM by Dr. Drang

Underscore David Smith wrote a post earlier this week that I had trouble with. Part of the trouble was that the code he wrote was in Swift, but that was a minor problem, as UDS’s code was clear enough to understand even though I don’t know Swift. The bigger problem was how he managed to transform an angle into a pair of xy coordinates without using any trigonometric functions. Once I figured it out, I saw that it was an interesting example of linearization without using the typical small angle approximation. So I decided to write this post.

Unsurprisingly, other people had the same trouble with UDS’s code, and this morning he published an updated post with their “corrections” to his transformation function. In some sense, these truly are corrections in that they provide a more accurate transformation. But UDS’s function is pretty accurate, probably accurate enough for his purposes, so they’re not necessarily correcting a mistake. Still, they presented some interesting ways of performing the transformation, and I’ll comment on them at the end of this post.

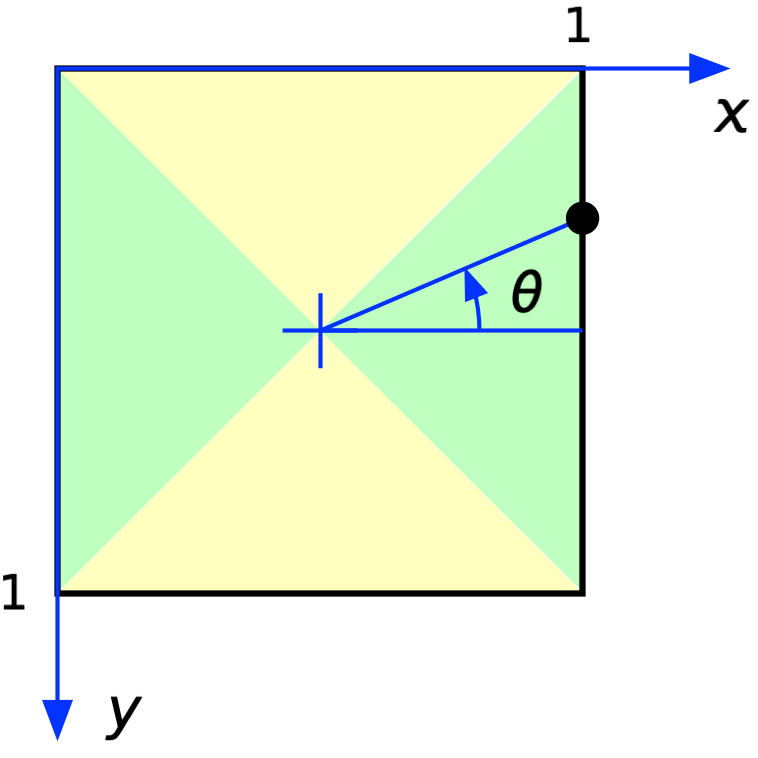
Let’s summarize Underscore’s problem. He wants to use Swift’s LinearGradient fill style for an arbitrary angle. Unfortunately, LinearGradient won’t accept an angle as its argument. It will, however, take a UnitPoint argument. A UnitPoint is a pair of coordinates on the perimeter of the unit square shown below,

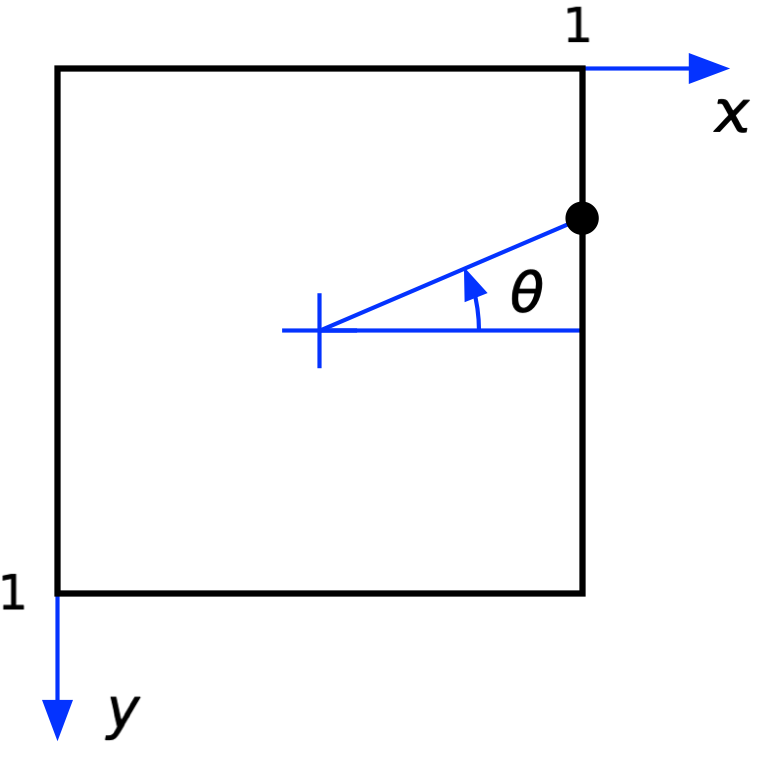
where I’ve also shown the angle that UDS wants to use as his input.

Getting $x$ and $y$ from $\theta$ is a fairly straightforward trig problem, although there’s some annoying bookkeeping necessary to deal with the corners. With the hope of avoiding that bookkeeping, I decided to look into conformal mapping from a disc onto a square. I didn’t have my copy of Churchill’s book handy, so I did some Googling and ran across this nice writeup by Chamberlain Fong. Fong shows several ways of mapping discs onto rectangles. Most important, he shows that conformal mapping (which can be very nasty mathematically) is unnecessary for our problem—we can use what he calls the Simple Stretching transformation.

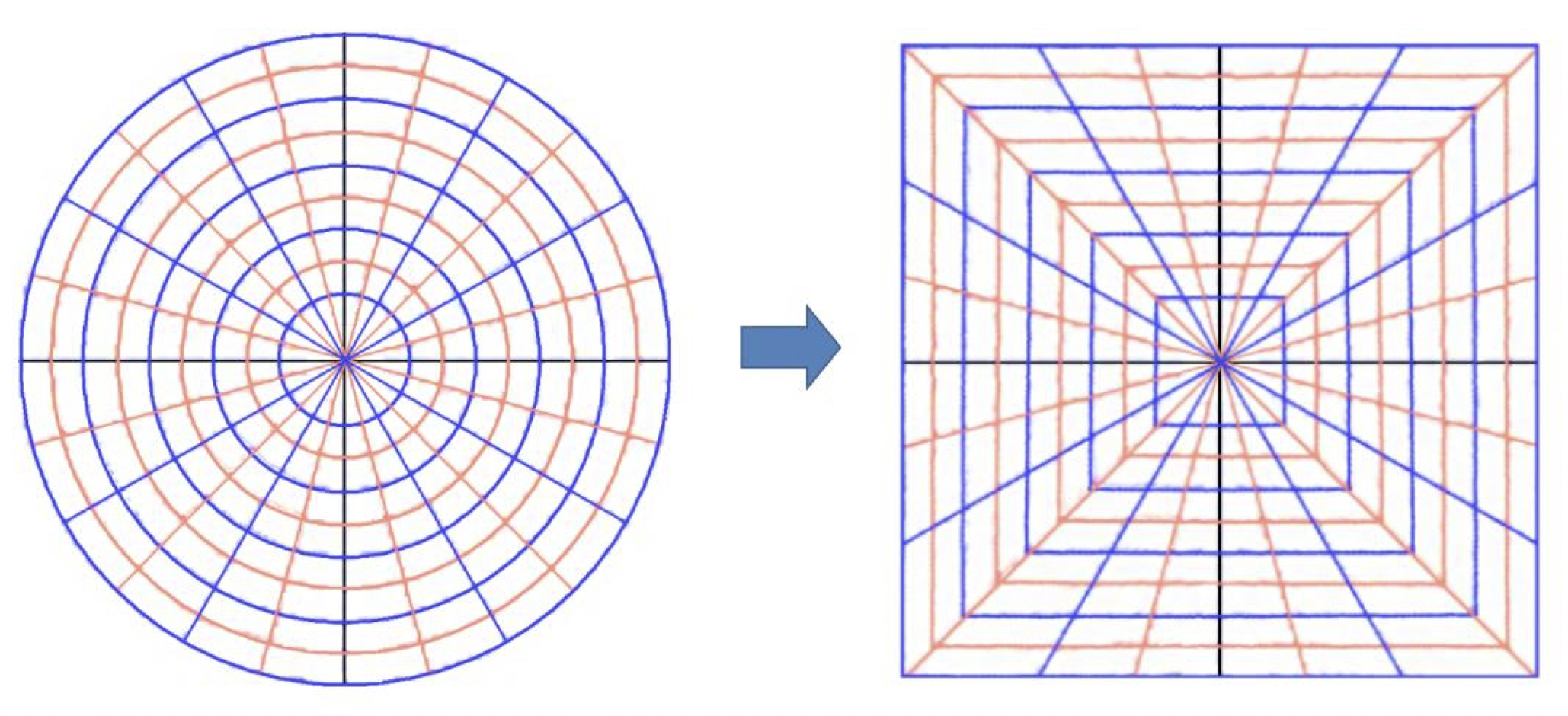
As you can see, the angles in the box are the same as those in the disc, which we’ll need to do what UDS wants. The transformation formulas Fong gives for this mapping (on p. 3 of his paper) work over the entire disc and square. We can specialize them for just the perimeter:

Here, $\mathrm{s}\mathrm{g}\mathrm{n}$ is the signum or sign function—it returns $+1$ if the argument is positive, $-1$ if the argument is negative, and zero if the argument is zero. The coordinate systems are shown below:

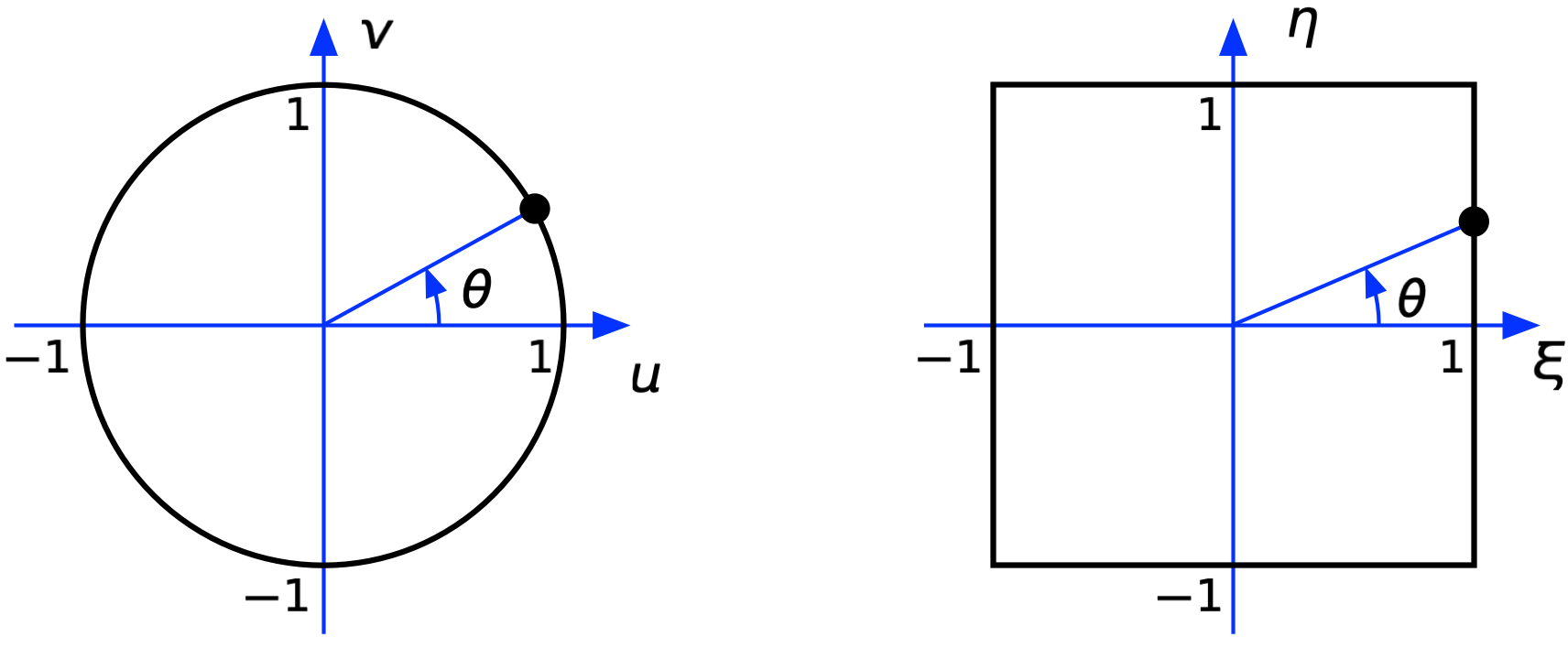
So what we have now is a series of transformations. First, we go from $\theta$ to $(u,v)$:

Then we go from $(u,v)$ to $(\xi ,\eta )$ using the formulas above. Finally, we go from $(\xi ,\eta )$ to $(x,y)$:

This last one is, I think, pretty obvious. We flip the vertical coordinate, then squeeze the 2×2 box into 1×1 and move its center from the origin to $(1/2,1/2)$.

You might be looking at this and thinking the bookkeeping I wanted to avoid would be easier than cascading three coordinate transformations like this. I guess it depends on what you’re used to. To me, putting one transformation after another after another is easier to remember than keeping track of which side of the box you’re on.

Before turning this into code, there’s a simplification we can make to the transformation from $(u,v)$ to $(\xi ,\eta )$. Note that

So the transformation equations can be changed to

where we’ve also noted that the ordering of the squares is the same as the ordering of the absolute values.

In Python (because I don’t know Swift), the three-part transformation from $\theta$ to $(x,y)$ is

python:
 1:  def xy(a):
 2:    # Coords on circle of unit radius with angle a (in degrees)
 3:    u = cosd(a)
 4:    v = sind(a)
 5:    
 6:    # Convert to coords on square from (-1, -1) to (1, 1)
 7:    if abs(u) >= abs(v):
 8:      xi = u/abs(u)
 9:      eta = v/abs(u)
10:    else:
11:      xi = u/abs(v)
12:      eta = v/abs(v)
13:    
14:    # Convert to coords on square from (0, 0) to (1, 1) with flipped
15:    # vertical axis
16:    return (1 + xi)/2, (1 - eta)/2

This is not necessarily the fastest implementation, or the shortest, but it’s pretty simple, and you can see each transformation in turn. Note that if you think of the $(\xi ,\eta )$ box as being divided into 90° sectors like this,

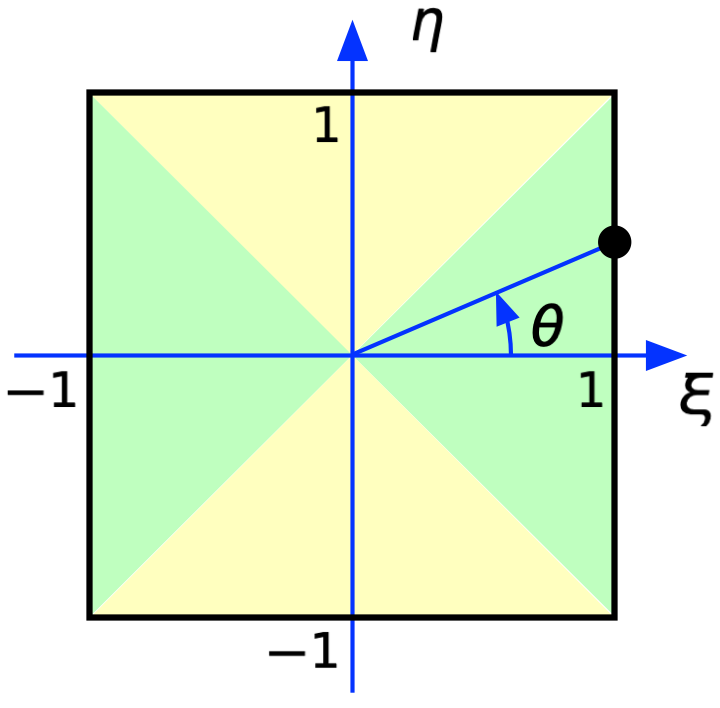
the green areas correspond to $|u|\ge |v|$ and the yellow areas correspond to $|u|<|v|$, which is how we split the if conditional.

python:
 1:  from math import sin, cos, tan, asin, acos, atan, atan2, degrees, radians
 2:  
 3:  def sind(x):
 4:    return sin(radians(x))
 5:  
 6:  def cosd(x):
 7:    return cos(radians(x))
 8:  
 9:  def tand(x):
10:    return tan(radians(x))
11:  
12:  def asind(x):
13:    return degrees(asin(x))
14:  
15:  def acosd(x):
16:    return degrees(acos(x))
17:  
18:  def atand(x):
19:    return degrees(atan(x))
20:  
21:  def atan2d(y, x):
22:    return degrees(atan2(y, x))

import * from trigd

So how does this compare with what Underscore does? Here’s his code:

func unitSquareIntersectionPoint(_ angle:Angle) -> UnitPoint {
var normalizedDegree = angle.degrees
while normalizedDegree > 360.0 {
    normalizedDegree -= 360.0
}
while normalizedDegree < 0.0 {
    normalizedDegree += 360.0
}
if normalizedDegree < 45.0 || normalizedDegree >= 315 {
    //Right Edge, x = 1.0
    var degreeToConsider = normalizedDegree
    if degreeToConsider < 45.0 {
        degreeToConsider = normalizedDegree +  360.0
        //angle now between 315 & 405
    }
    let degreeProportion = (degreeToConsider - 315.0) / 90.0
    return UnitPoint(x: 1.0, y: 1.0 - degreeProportion)
} else if normalizedDegree < 135.0 {
    //Top Edge, y = 0.0
    let degreeProportion = (normalizedDegree - 45.0) / 90.0
    return UnitPoint(x: 1.0 - degreeProportion, y: 0.0)
} else if normalizedDegree < 225.0 {
    //left Edge, x = 0.0
    let degreeProportion = (normalizedDegree - 135) / 90.0
    return UnitPoint(x: 0.0, y: degreeProportion)
} else if normalizedDegree < 315.0 {
    //Bottom Edge, y = 1.0
    let degreeProportion = (normalizedDegree - 225) / 90.0
    return UnitPoint(x: degreeProportion, y: 1.0)
}
return .zero
}

(Sorry, I don’t have syntax highlighting set up here for Swift.)

As you can see, he splits his calculations into the four colored sectors—now on the unit square—but he has to treat all four sectors separately

The main difference, though, is that he doesn’t use trig functions. For each side of the square, he sets one of the coordinates to 0 or 1, as appropriate, and sets the other as

where $\varphi$ is the angle from the closest corner clockwise from $\theta$. In other words, to get the y coordinate along the right edge, $\varphi$ is measured from the bottom right corner; to get the x coordinate along the top edge, $\varphi$ is measured from the top right corner; and so on.

In my xy function, the key calculations are

which give us $\pm 1$ for the first two and either $\pm \cot \theta$ or $\pm \tan \theta$ for the other two. My $\pm 1$ correspond to UDS’s 0 and 1.¹ And since

and tangent repeats every 180°, my other calculations always return a result equivalent to the tangent of an angle between -45° and +45°.

The upshot is that UDS’s function is approximating the tangent like this,

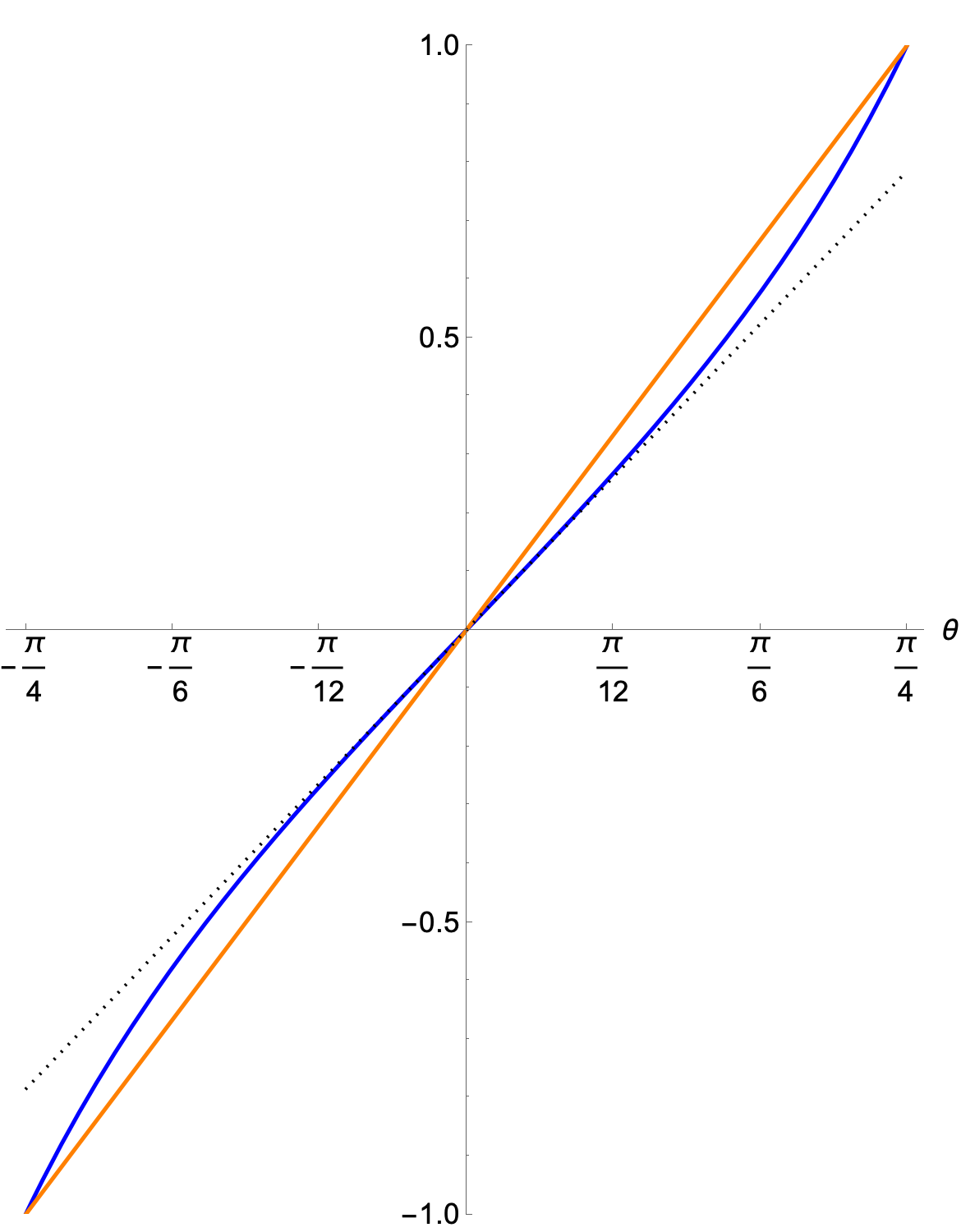
where the blue line is the tangent and the orange line is UDS’s approximation. As you can see, they’re fairly close to each other.

You’ll notice I’ve plotted $\theta$ in radians. That’s because I also wanted to show the usual small angle approximation of tangent,

which I’ve plotted as the dotted black line. The small angle approximation works only when the angle is given in radians.

As expected, the small angle linear approximation gets crappy as you get further from 0°. By tilting his approximating line, UDS gets perfect alignment at the corners and midsides of the box (the most important places) and decent alignment elseswhere.

How decent? Let’s plot the angle associated with UDS’s output and compare it to the input angle:

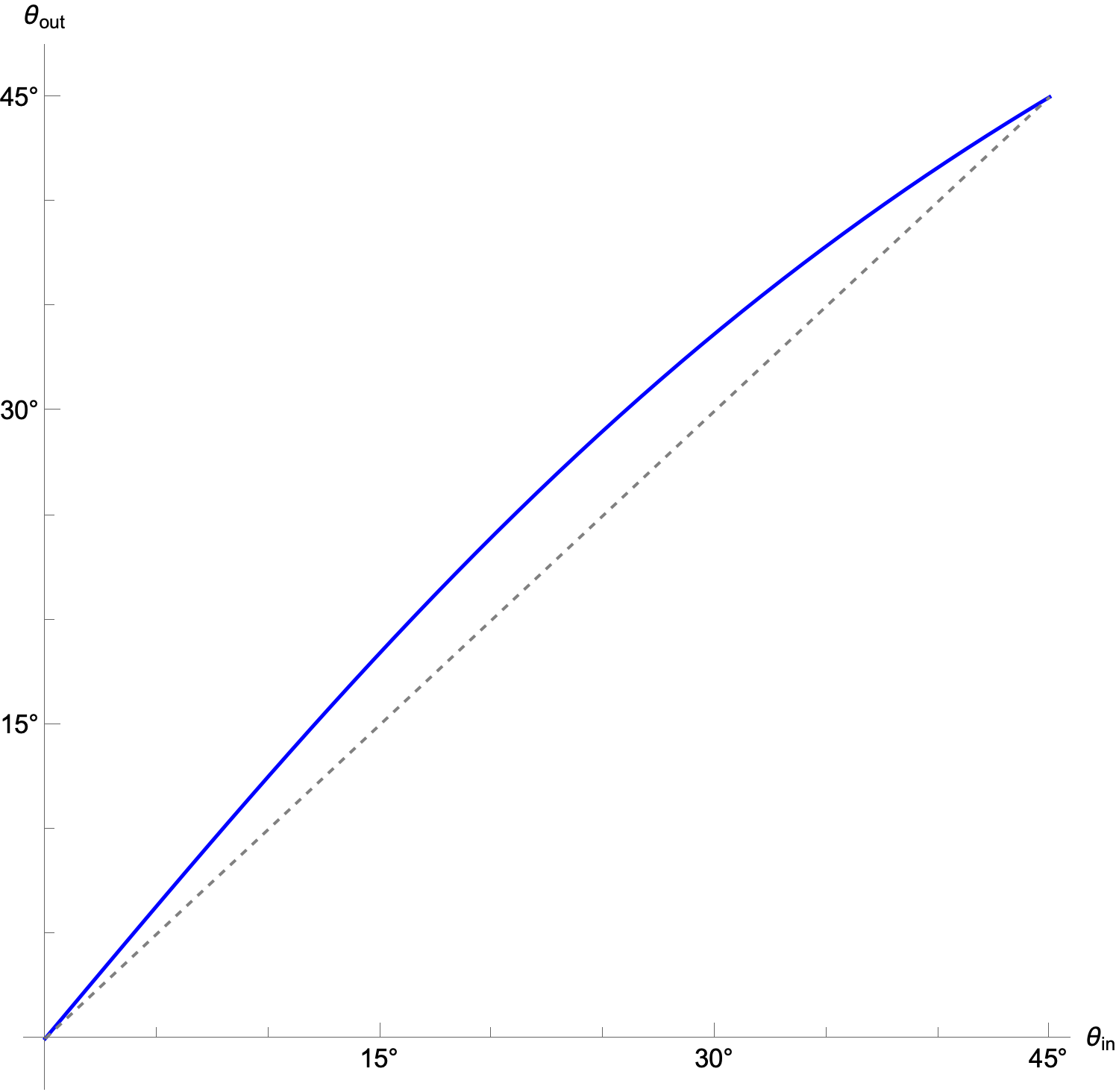
The symmetry (actually antisymmetry) means we can restrict ourselves to 0° to 45°. The dashed line is what the plot would look like if Underscore’s function wasn’t doing an approximation.

Here’s a plot of the error:

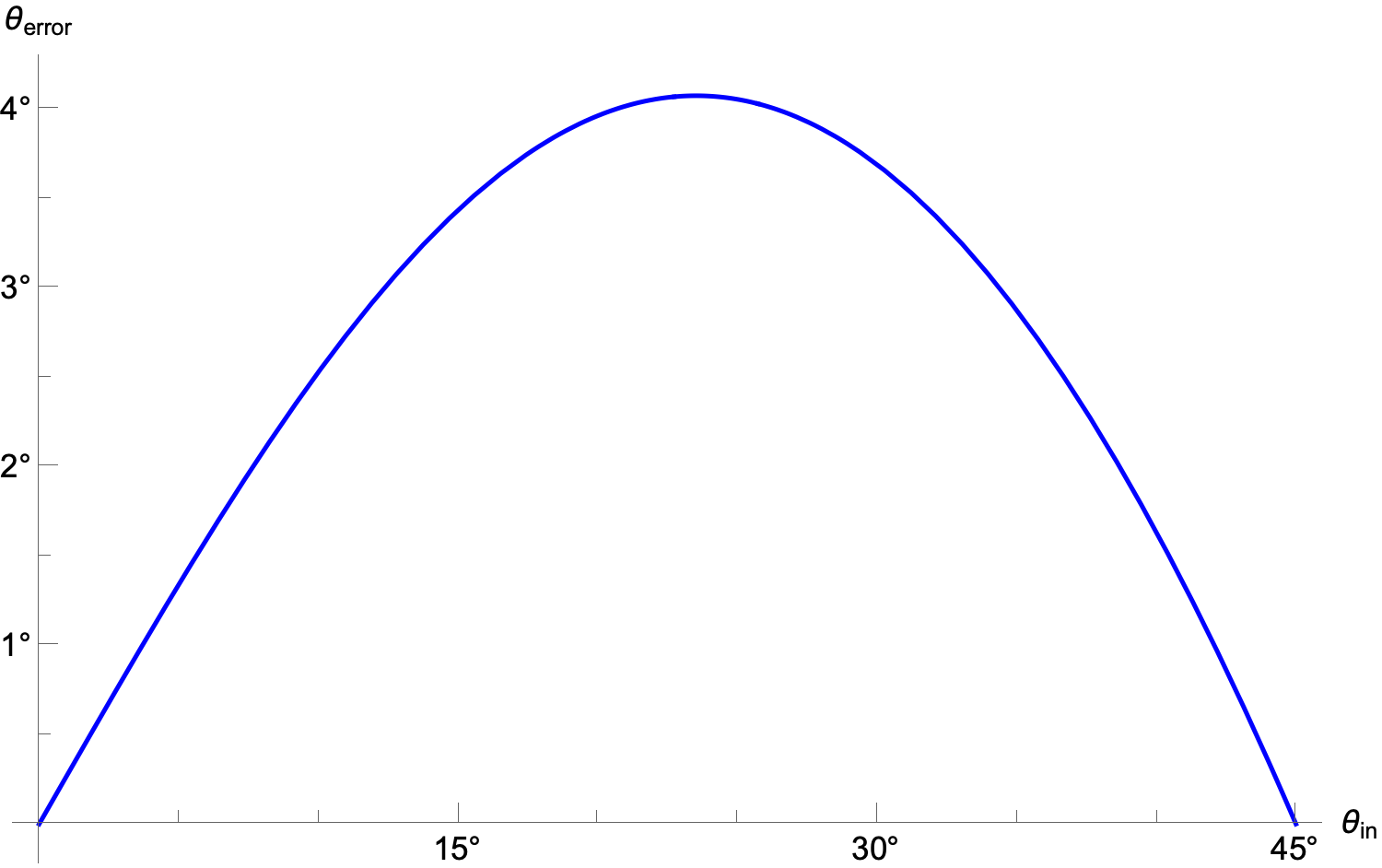
It’s not a parabola, nor is it symmetric, but it’s close. The maximum error is 4.07° when the input angle is 23.52°

Is a maximum error of 4° acceptable? I suspect it is, especially because of where it occurs. People tend to be better at detecting angular errors near the horizontal, vertical, and 45° than they are at other angles.² UDS’s function is good where it needs to be and less good where it doesn’t.

On the other hand, it could well be argued that this is not an especially time-critical calculation, and you might as well do the trig calculations³ instead of estimating through proportions. A lot depends on what sort of calculations you’re most comfortable with.

Which brings us to Underscore’s update and the “corrections” therein. Most of them include code that looks a lot like mine, which isn’t surprising, since they’re doing the same sort of trigonometry I am. Math is math. But there are some interesting variations.

DrewFitz does two thing I like:

1. They start by changing the sign of the angle, which has the effect of flipping the vertical coordinate without flipping the horizontal coordinate because sine is antisymmetric and cosine is symmetric.
2. They determine the maximum of $|u|$ and $|v|$, and uses that as his denominator. This eliminates the if/else clause (it’s still under the hood of the max function, but you don’t see it).

Sometimes being clever like this gets you in trouble, but I think the comments in the code explain what’s going on quite well.

robb’s solution is very close to mine and even closer to the equations in Fong’s paper. Like DrewFitz, robb tweaks the angle upon input to handle the flipping of the vertical axis, but in this code the angle is increased by 90° and the sine and cosine are reversed. That tweak was a little harder for me to understand, but it works.

Like Underscore, I find Rob Mayoff’s solution hard to understand. Mayoff uses a combination of max, min and copysign (which takes the place of signum) to deal with the sector choice. It works, but I would have a hard time explaining why without going through numerical examples. Also, I think they’re using an opposite sign convention for the angle—UDS’s increases counterclockwise while Rob Mayoff’s seems to increase clockwise—but that’s a minor issue.

Of course, I think my solution is the “best” (followed closely—maybe edged out?—by DrewFitz’s) but that’s because it fits my way of thinking. As we learn more, our ways of thinking change and “best” changes, too. That’s why you’re constantly told to comment your code.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang